- •1. Инженерлік графика нені зерттейді және оның негізгі мақсаттары
- •2. Монж әдісі ,Проекциялық жазықтықтар
- •3. Ортогональді проекциялау Сандық өлшеулері бар проекциялар
- •4. Октанттар. Екі проекциялық жазықтықтағы нүктенің ортогональді проекциясы
- •5. Позициялық және метрикалық есептер
- •4.1.1 Нүкте мен түзу сызықтың өзара орналасулары
- •4.1.2 Түзу сызықтардың өзара орналасулары
- •4.1.3 Екі жазықтықтың өзара орналасуы
- •4.1.4 Түзу мен жазықтықтың өзара орналасулары
- •4.2 Метрикалық есептер
- •4.2.1 Түзу сызықтың нақты шамасы мен жазықтыққа жасайтын бұрышы
- •7.Түзусызық. Түзусызықтың графикалық берілу әдісі. Проекция жазықтығына қатысты түзу сызықтың орналасуы
- •1. Параллель түзулер .
- •2. Қиылысатын түзулер.
- •12. Екі түзудің өзара орналасуы
- •13. Ортогональды проекцияларды түрлендірулердің әдістері
- •14 Ортогональды проекцияларды түрлендірулердің әдістері
- •14.Проекциялар жазықтығына препендикуляр өс бойынша айналдыру әдісі
- •15.Ортогональды проекцияларды түрлендірулердің әдістері
- •17. Нүкте мен түзудің өзара орналасуы
- •18. Түзу сызықты кесіндіні берілген қатынасқа бөлу
- •19. Орталық проекциялау
- •20. Нүкте үш проекция жазықтықтарының ортогональды жүйесінде
- •21. Ортогоналдық проекцияларды түрлендіру әдістері.Проекция жазықтықтығына параллел өсі бойынша айналдыру әдісі
- •21.Проекциялар жазықтығына параллель өс бойынша
- •23 Жазықтық. Жазықтықтың графикалық берілу әдістері
- •24 Проекция жазықтығына қатысты жазықтықтың әртүрлі орналасуы
- •25. Жазықтықтың ізі
- •26. Жазықтыққа перпендикуляр түзу сызық
- •27. Нүкте мен жазықтықтың өзара орналасуы
- •28. Түзу мен жазықтықтың өзара орналасулары
- •29. Екі жазықтықтың өзара орналасуы.
- •30. Түзудің іздері.
- •31. Жазықтыққа перпендикуляр туралы теорема
- •32. Параллель проекциялау əдісі
- •32 Паралель проекция.
- •33.Түзудің жазықтыққа қатысты орналасуы
- •34. Проекция жазықтығына байланысты жазықтықтың әр түрлі болып орналасуы
- •36. Жазықтықтардың негізгі әдістері
- •37.Көпжақтылар
- •38. Көпжақтылар мен жазықтықтардың қиылысуы.
- •39. Түзудің көпжақтылармен қиылысуы
- •40. Көпжақты беттердің өзара қиылысуы
4.2.1 Түзу сызықтың нақты шамасы мен жазықтыққа жасайтын бұрышы
Егер түзу сызық кеңістікте жалпы жағ дайда орналасқан болса, онда оның көлденең П0 жазықтығындағы проекциясы бұрмаланып, түзу сызық ұзын немесе қысқа болып кескінделеді. Сандық белгісі бар проекцияларда жалпы жағдайда берілген түзу сызықтың нақты шама сын (ұзындығын) табу үшін, берілген А4В6 түзуінің А4 жəне В6 нүктелерінен түзуге перпендикуляр сызық жүргіземіз. Осы сызық бойына сан өлшемдерін өлшеп саламыз. Егер табылған А жəне В нүктелерін өзара қоссақ, онда жүргізілген түзу сызық ұзындығы түзудің нақты шамасы болады (48-сурет).
4.2.2 Нүкте мен жазықтықтың арақашықтығы Жоғарыда айтып кеткендей, метрикалық есептер деп гео метриялық фигуралардың сыз бал ары арқылы олар дың кеңіс тік тегі өзара қашық тықтарын анық тайтын есептерді айтады.
7.Түзусызық. Түзусызықтың графикалық берілу әдісі. Проекция жазықтығына қатысты түзу сызықтың орналасуы
Түзу сызық дегеніміз - бір түзу бойындағы нүктелер жиынтығы. Мектеп бағдарламасында геометрия пəнінен өткендей, бір нүктеден басталып сызылған түзуді сəуле дейміз. Ал екі нүктеден өткен түзуді кесінді дейміз. Сызба геометрияда түзу сызықтар нүктелер жиынтығы болғандықтан, түзу Түзу сызық. Түзудің графикалық бейнелену түрлері.
Түзу сызық геометрияның негізгі түсініктерінің бірі болып табылады. Егер геометрияны тұрғызу негізінде кеңістіктегі екі нүктенің арақашықтық түсінігі қарастырылатын болса, онда түзуді екі нүктенің ең кіші арақашықтығы ретінде қарастыруға болады.
Түзу сызық сызықты алгебрада бірінші ретті сызық болып табылады. Түзудің жалпы теңдеуі:
Ах+Ву+С=0,
А, В және С – кез-келген тұрақтылар.
Проекция жазықтықтарына қатысты түзудің орналасуына байланысты жеке немесе жалпы жағдайларын қарастыруға болады.
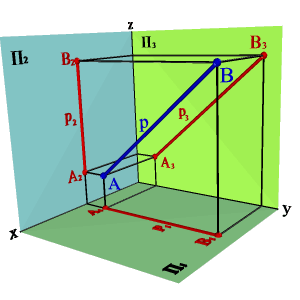
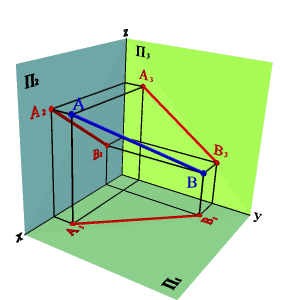
1. Проекция жазықтықтарының ешбіріне параллель емес түзу жалпы жағдайдағы түзу деп аталады (3.4. - сурет).
|
|
|
|
2. Проекция жазықтықтарына параллель түзулерді жеке жағдайдағы түзулер ретінде қарастыруға болады және оларды деңгейлік түзулер деп атайды. Берілген түзуді қай жазықтыққа параллель екеніне байланысты ажыратады:
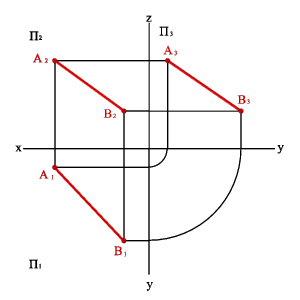
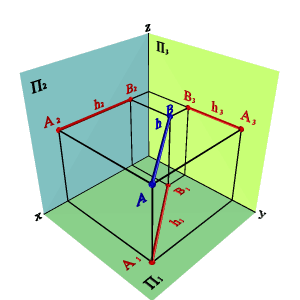
2.1. Горизонтальды проекция жазықтығына параллель түзу горизонталь түзу немесе горизонталь деп аталады (3.5. - сурет). Кез-келген горизонталь нүктелер жұбына мына теңдеу сәйкес келеді:
zA=zB Þ A2B2//Ox; A3B3//Oy Þ xAxB#0, yAyB#0, zAzB=0.
|
|
|
|
2.2. Фронталь проекциялар жазықтығына параллель түзулер фронталь деп аталады (3.6. - сурет).
yA=yBÞ A1B1//Ox, A3B3//Oz Þ xAxB#0, yAyB=0, zAzB#0.
|
|
|
|
2.3. Профилді проекция жазықтығына параллель түзу профиаль деп аталады (3.7. - сурет).
xA=xBÞ A1B1//Oy, A2B2//Oz Þ xAxB=0, yAyB#0, zAzB#0.
|
|
Түзу сызықтың өзара орналасуы.
Түзу сызықтар кеңістікте параллель, қиылысатын
және айқас болуы мүмкін.

 3.4.
-
Сурет.
Жалпы жағдайдағы түзу
3.4.
-
Сурет.
Жалпы жағдайдағы түзу
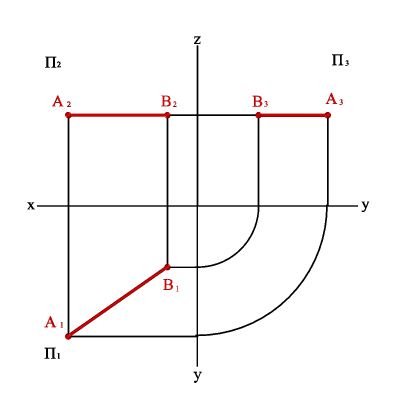 3.5.
-
Сурет. Горизонталь
түзу
3.5.
-
Сурет. Горизонталь
түзу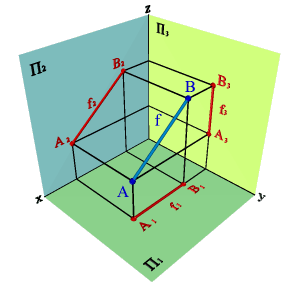
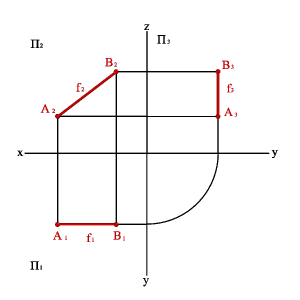 3.6.
-
Сурет. Фронталь
түзу
3.6.
-
Сурет. Фронталь
түзу