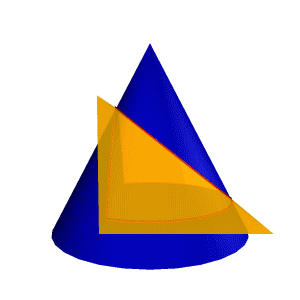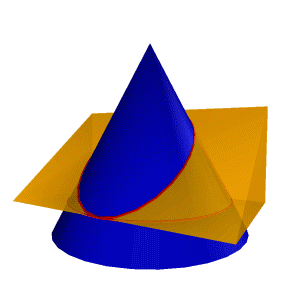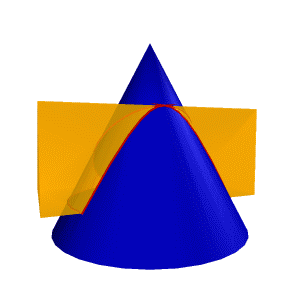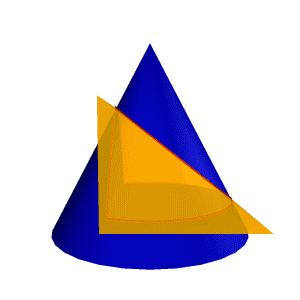38. Көпжақтылар мен жазықтықтардың қиылысуы.
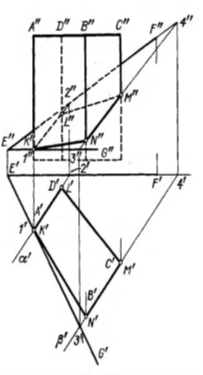
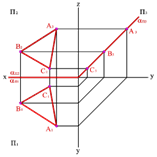
Пирамида мен призманың түзумен және жазықтықпен қиылысуы. Көпжақтының жзықтықпен қиылысуын көрсету үшін көпжақтының қабырғаларының жазықтықпен қиылысу нүктесін табу керек. Келесі суретте призманың EF және EG қиылысқан түзулерімен қиылысуы көрсетілген. Жазықтықты 𝛿 деп белгілейік. Қиылысу кезінде төбесі 𝛿 жазықтығы мен призма қабырғасының қиылысу нүктесі болатын төртбұрыш болып табылады. Бұл жағдайда тік призма және ол горизонталь проекциялық жазықтыққа паралель болғандықтан оның 𝜋1 жазықтықтағы қиылысуы тез табылады. A және D нүктесі арқылы өтетін призманың қабырғасы 𝛿 жазықтығымен қиылысатын К және L нүктесін табуға болады. Призманың қабырғалары арқылы өтетін 𝛼 және 𝛽 қосымша жазықтықтарды жүргізіп KL және MN кесінділері арқылы қиылысуды көрсетуге болады. Фронталдық проекцияда қиылысу кесінділері көрінетін және көрінбейтін жақтары болады.
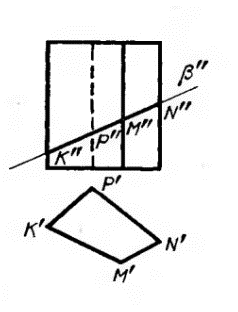
Егер де қиатын жазықтықтың біреуі проекциялық жазықтықтың біреуіне перпендикуляр болса (төмендегі суреттегідей), онда қиылысу проекциясы қосымша тұрғызусыз болады. 𝐾′′ 𝑃′′ 𝑀′′ 𝑁′′ фронталдық проекциясы 𝛽 жазықтығының ізінде орналасады, ал горизонталдық проекциясы 𝐾′ 𝑃′ 𝑀′ 𝑁′ призманың проекциясымен сәйкес келеді.
Көпжақтылардың жазықтықпен қиылысуының 2 әдісі бар:
1. Қиюшы жазықтықтың көпжақтардың әрбір жағымен қиылысуы – қиылысу сызықтары кобжақтардың әрбір жақтарынан тыс жатпайды.
2. Қиюшы жазықтықтың көпжақтылардың қабырғаларымен қиылысуы
36. . Жазықтықтарды салу әдістері. Жазықтықтың проекциялық жазықтыққа катысты орналасуы.
Жазықтықтарды салудың төрт әдісі:
1) бір түзудің бойында жатпайтын үш нүкте арқылы;
2) түзу және түзу бойында жатпайтын нүкте арқылы;
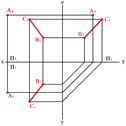
3) паралель түзулер арқылы;
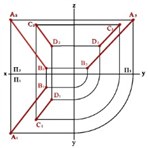
4) қиылысатын түзулер арқылы.
Еш проекциялық жазықтыққа перпендикуляр болмайтын жазықтықты ортақ жағдайдағы жазықтық деп атайды.
Горизонталь проекциялық жазықтыққа перпендикуляр жазықтықты горизонталь проекциялаушы жазықтық деп атайды.
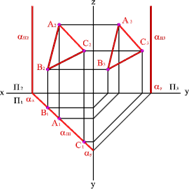
Фронталь проекциялық жазықтыққа перпендикуляр жазықтықты фронталь проекциялаушы жазықтық деп атайды.
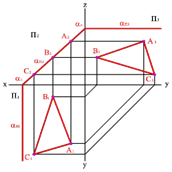
Профильді проекциялық жазықтыққа перпендикуляр жазықтықты профильді проекциялаушы жазықтық деп атайды.
39. Түзудің көпжақтылармен қиылысуы
1 Мысал: Конуспен үшбұрышты призманың қиылысу сызығын тұрғызуды қарастырамыз (8.31.сурет) Конустың айналу өсі . П1 жазықтығына перпендикуляр, ал призма жақтары П2 жазықтығына перпендикуляр. Бұл жағдайда Призманы оның жақтары арқылы өтетін α, β, γ үш жазықтық ретінде қарастыруға болады, ал есеп жазықтықпен конустық қиылысу сызықтарын табуға әкеледі. |
|
Сонымен α жазықтығы конусты П1 ге параллель шеңбер бойынша қияды, β П3 –ке параллель гипербола бойынша, ал γ – эллипс бойынша.
Барлық жазықтықтың қиылысу сызығы П2 жазықтығына α, β, және γ жазықтығының ізімен сәйкес келетін түзуге проекцияланады.
Бұл сызықтың П1 және П3 жазықтықтарында проекцияларын тұрғызу үшін қиылысу сызықтарының фронталь проекцияларында сипаттаушы гүктелерін белгілейміз:
12 және 62 – П2 жазықтығындағы конус очеркісінің проекциясымен γ жазықтығының қиылысу нүктелері, бұл нүктелер эллипстің үлкен өсінің орналасу жағдайын анықтайды, 12 нүктесінің проекциясы гипербола төбесі және біруақытта конусқа, призма қабырғасына тиісті ал 62- нүктесі біруақытта конусқа және призма қабырғаларына тиісті нүкте проекциясы 2, 3, 7 және 8 нүктелерінің профильді проекциялары конус проекцияларының очеркісінде жатыр; 42, 52- нүктелері 1262 кесіндісінің ортасында жатыр (эллипстің үлкен өсінде жатыр) және эллипстің кіші өсінің орналасу жағдайын анықтайды; 9,10 – нүктелері біруақытта конусқа және призмаға тиісті (α және β жазықтықтарының қиылысуымен құралған).
4 және 5 нүктелерінің проекцияларын табуды қарастырайық. Бұл нүктелердің фронтальды проекциялары арқылы φ көмекші қиюшы жазықтығын жүргіземіз. Бұл жазықтық конусты p паралелі бойынша қияды, ал призма жағын қабырғаға параллель m түзу сызығы бойынша. p 1 және m 1. қиылысуының горизонталь проекциялар жазықтығында 41 және 51 нүктелерінің орналасу жағдайын анықтайды.