36. Жазықтықтардың негізгі әдістері

Жазықтықтардың құрастыру әдісінің екі негізгі түрі бар – сызықтың немесе жазықтықтың қозғалуымен қарастырайық, бұл жағдайда ф жазықтығы көптеген жағдайда орналасады l¹, l², қозғалысы мен пішіні кейбір заңдарға сүйенеді. Бұл сызықты құраушы деп атайды.

Құраушының пішініне және оның жазықтық кеңістігіндегі орнын ауыстыру заңына байланысты жеке топтарға бөлуге болады.

Сызықтық жазықтықтар – бұл түзу сызық арқылы жасалынатын жазықтықтар.

Сызықтық емес жазықтықтар – бұл тек қана қисық сызық арқылы пайда болатын жазықтықтар.

Жазбалы жазықтықтар – бұл құраушының қимасынан кейін жазықтықпен үзіксіз және қатпарсыз ұйқас болатын жазықтықтар.

Жазылмайтын жазықтықтар – бұл жазықтықпен үзіксіз және қатпарсыз ұйқас бола алмайтын жазықтықтар.

Қалыпты құраушы жазықтықтар – бұл құраушысы жазықтықтың түрлендірілу барысында өзінің пішінін өзгерпейтін жазықтықтар.

Қалыпсыз құраушы жазықтықтар – бұл құраушысы жазықтықтың түрлендірілу барысында өзінің пішінін өзгертетін жазықтықтар.

37.Көпжақтылар

Көпжақтылар дегеніміз бір мезгілде әр жағы екіншінің жағы болатын жазық көпбұрыштылардың жиынтығын айтады.

көпбұрыштылардың жиынтығын айтады. Пирамида – бір жағы көпбұрышты ал қалғандары төбесі бір үшбұрышты болып табылатын көпжақты.

Егер негізінде дұрыс көпбұрышты жатса және пирамиданың биіктігі көпбұрыштының центрі арқылы өтсе, пирамида дұрыс болады. Егер төбесі жазықтықпен қиылған болса, қиылған пирамида болады

Призма – екі қабырғасы паралель орналасқан көпбұрыштыдан ал қалған қабырғалары паралелограмм болып табылатын көпжақты. Призма тікбұрышты болады егер оның қабырғалары негізіне перпендикуляр болса. Егер призманың негізі тікбұрышты болса призманы параллелепид деп атайды.

Призматоид – паралель орналасқан екі көпбұрытымен шектелген көпжақтыны айтады. многогранник, жақтары трапеция немесе үшбұрыш болады, төбелері көпжақтының негізінің төбесіне сәйкес келеді.

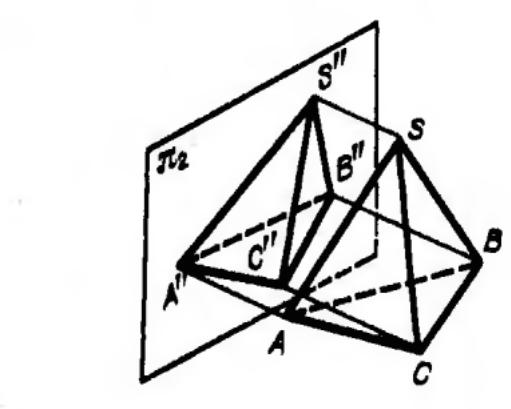
Көпжақтыларды проекциялық жазықтықта салу үшін олардың нүктелерінің проекцияларын салу керек. Мысалы SABC пирамидасын проекциялық жазықтыққа салу үшін оның S, А,В және С төбелерін салып, осы нүктелерді қоса отырып АВС, SВС, SАС жақтарын аламыз.

Мысалы қандай да бір берілген призманың жақтарының жазықтықпен қиылысуы белгілі болсын. Призманы екі паралель жазықтықпен қиылыстырып призманың негізін алуға болады. Призманы қандай да бір паралель жатқан жазықтыққа салғанда оның шынында да призма екендігін қалай білуге болады? Егер жазықтықта түзу кесінділердің проекциялары берілсе, олар көпжақтының қабырға қызметін атқарады. кейде призма немесе паралелепид деп нақты айтуға болмайтын жағдайлар болады

.

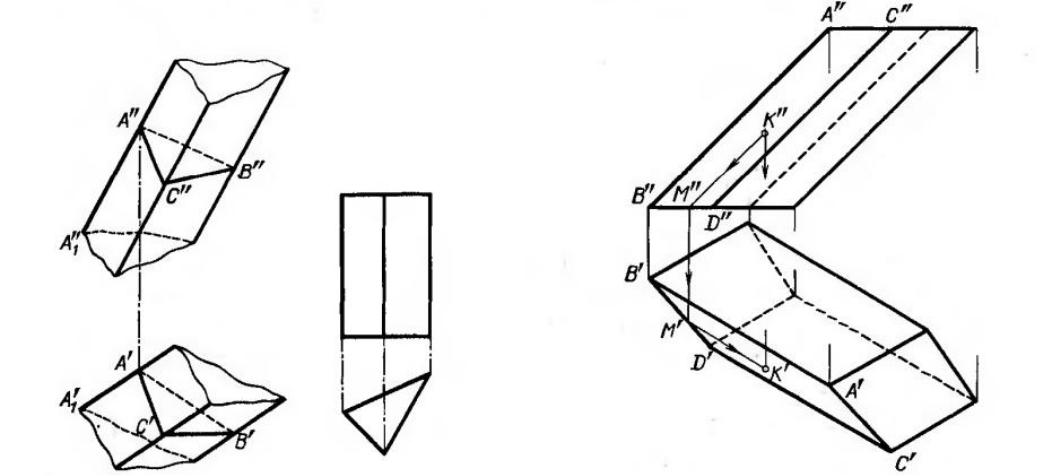
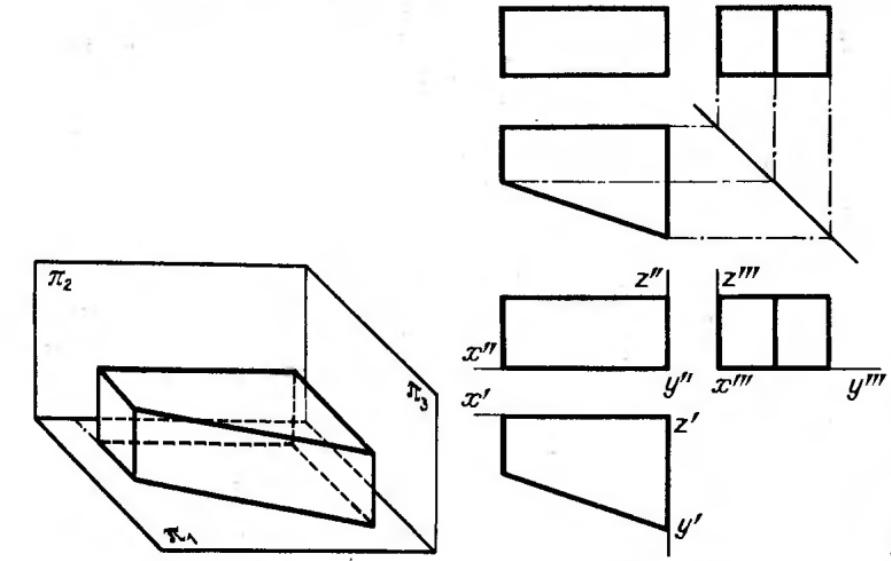
Енді осылардың нақ қайсысы екенін білу үшін профильді проекциясын көрсеткен жөн болар. Яғни кей жағдайларда көпбұрыштыларды екі проекциялық жазықтықта көрсету жеткіліксіз. Келесі суретте бұрыс призма және оның профильді проекциясы берілген.

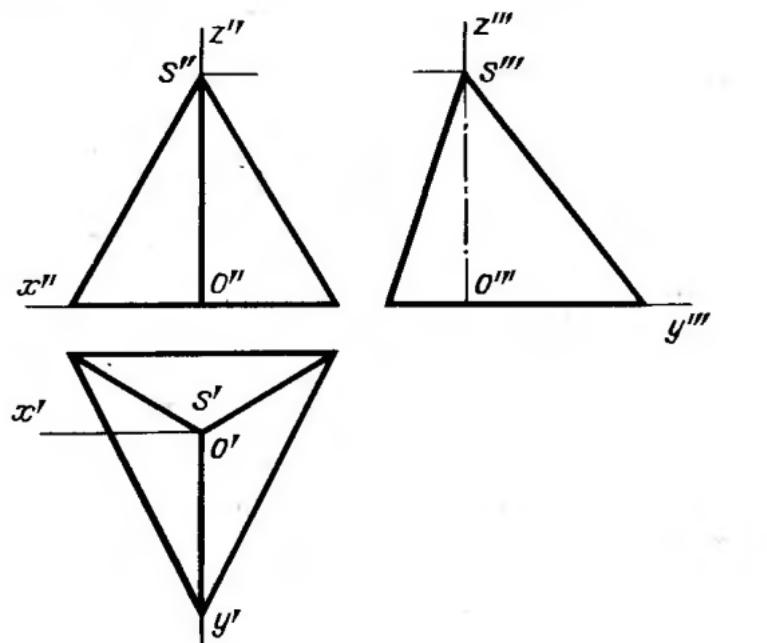
Пирамиданы жазықтықта салу үшін оның қабырғаларының жазықтықпен қиылысуын және олардың қиылысу нүктелерін көрсету керек. Суретте горизонтал және фронталь проекциялық жазықтықта пирамиданың проекциясы берілген. Пирамида үшін екі проекциялық жазықтық жетккілікті, себебі бір проекциялық жазықтықта оның негізі жатыр.

Көпжақтылар

Жазық көпбұрыштардың жиынтығы көпжақтар деп аталады, олардың әрқайсының әр жағы бір уақытта басқасының жағы болады (тек қана біреуінің).

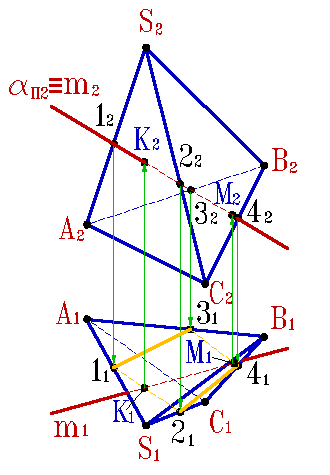
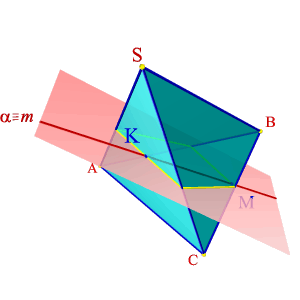
Түзу сызық пен көпжақтың қиылысу нүктесін анықтау үшін, түзу мен жақ жазықтықтарынң қиылысу нүктесіне алып келеді (6.12. - сурет).

Есепті шешу алгоритмі: 1. a: mÎa жазықтығын жүргізу; 2. a жазықтығымен көпжақтың қиылысуын тұрғызу. m түзуімен қиылысу кезінде алынған К, М –қиылысу нүктелерін анықтау
6.12. - Сурет. Түзу сызық пен пирамиданың қиылысуы