23 Жазықтық. Жазықтықтың графикалық берілу әдістері

Жазықтық – геометрияның негізгі түсініктерінің бірі болып табылады. Жазықтық алгебрада бірінші ретті бет, декартты координаттар жүйесінде жазықтық 1-дәрежелі теңдеумен берілуі мүмкін. Жазықтықтың жалпы теңдеуі:

Ax+By+Cz+D=0, мұндағыА, В, С, және D - түрақтылар, А, В және С бір уақытта нөлге тең емес.

Жазықтық — геометрияның негізгі ұғымдарының бірі. Геометрияның жүйелі курсын тұжырымдағанда жазықтық ұғымы бастапқы ұғым ретінде алынады, ал оның жанама анықтамасы геометрия аксиомаларында беріледі. Жазықтықтың кейбір сипаттамалық қасиеттері мынадай:

1. егер түзудің екі нүктесі жазықтықта жатса, онда түзудің барлық нүктелері сол жазықтықта жатады;

2. жазықтық — берілген екі нүктеден бірдей қашықтықтағы нүктелердің жиыны. :азықтық — бірінші реттік алгебралық бет. Ол декарттық координаттар жүйесінде 1-дәрежелі теңдеумен берілуі мүмкін. Жазықтықтың жалпы (толық) теңдеуі былай өрнектеледі: Ax+By+Cz+D=0, мұндағы A, B, C, D — тұрақтылар

1 Жазықтықтардың негізгі әдістері

Жазықтықтардың құрастыру әдісінің екі негізгі түрі бар – сызықтың немесе жазықтықтың қозғалуымен қарастырайық, бұл жағдайда ф жазықтығы көптеген жағдайда орналасады l¹, l², қозғалысы мен пішіні кейбір заңдарға сүйенеді. Бұл сызықты құраушы деп атайды.

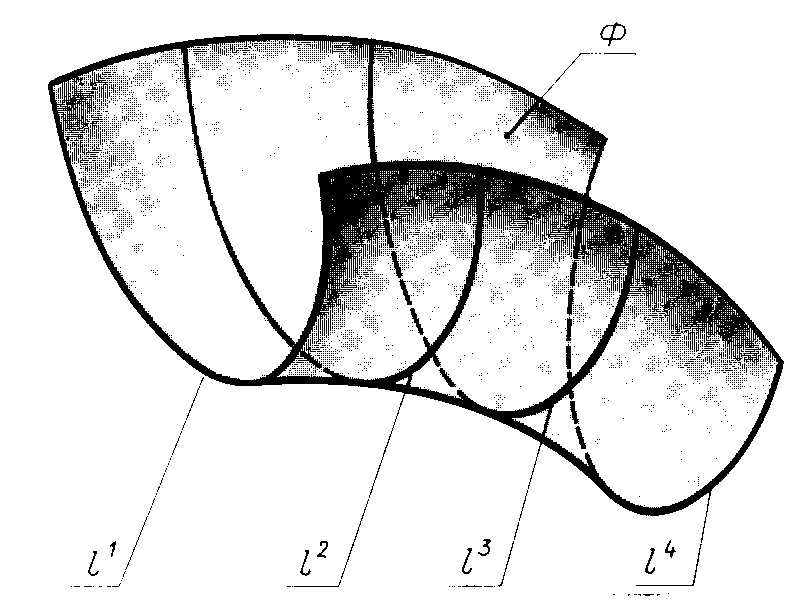
Құраушының пішініне және оның жазықтық кеңістігіндегі орнын ауыстыру заңына байланысты жеке топтарға бөлуге болады.

Сызықтық жазықтықтар – бұл түзу сызық арқылы жасалынатын жазықтықтар.

Сызықтық емес жазықтықтар – бұл тек қана қисық сызық арқылы пайда болатын жазықтықтар.

Жазбалы жазықтықтар – бұл құраушының қимасынан кейін жазықтықпен үзіксіз және қатпарсыз ұйқас болатын жазықтықтар.

Жазылмайтын жазықтықтар – бұл жазықтықпен үзіксіз және қатпарсыз ұйқас бола алмайтын жазықтықтар.

Қалыпты құраушы жазықтықтар – бұл құраушысы жазықтықтың түрлендірілу барысында өзінің пішінін өзгерпейтін жазықтықтар.

Қалыпсыз құраушы жазықтықтар – бұл құраушысы жазықтықтың түрлендірілу барысында өзінің пішінін өзгертетін жазықтықтар.

24 Проекция жазықтығына қатысты жазықтықтың әртүрлі орналасуы

Средний

№2

14.03.2014 18:50:33

ЖАЗЫҚТЫҚТАР

Жазықтықтарды салудың төрт әдісі:

1. бір түзудің бойында жатпайтын үш нүкте арқылы;

2. түзу және түзу бойында жатпайтын нүкте арқылы;

3. паралель түзулер арқылы;

4. қиылысатын түзулер арқылы.

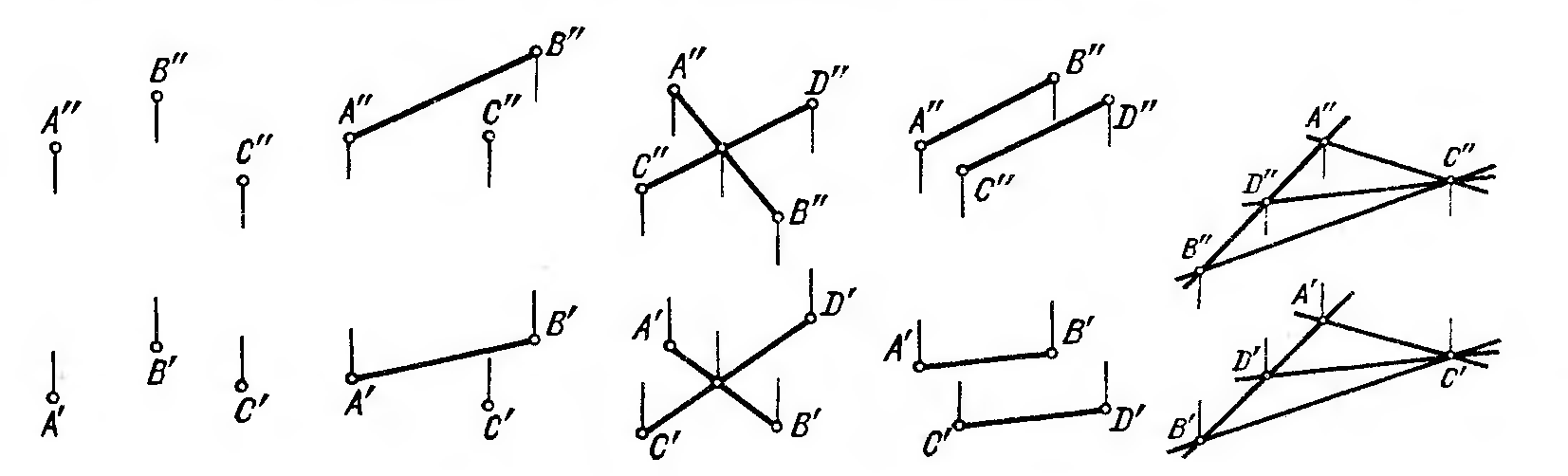
Жазықтық сызуда әр түрлі формада болуы мүмкін: төртбұрыш, шеңбер, квадрат, үшбұрыш ж.тб.

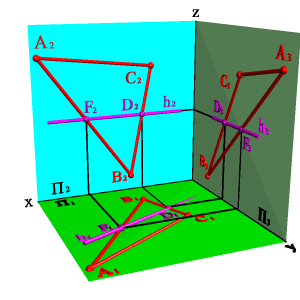
Жазықтықтың проекция жазықтыымен қиылысу түзуін жазықтықтың ізі деп атаймыз.

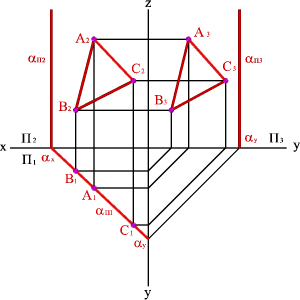
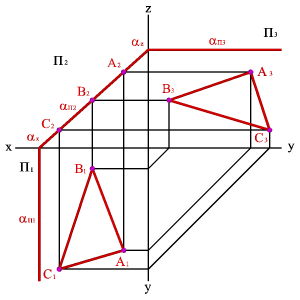
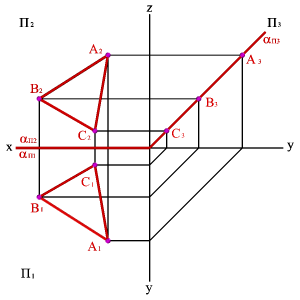
Суретте екі АВ және ВС қиылысқан түзулері арқылы берілген жазықтықтың ізі көрсетілген.

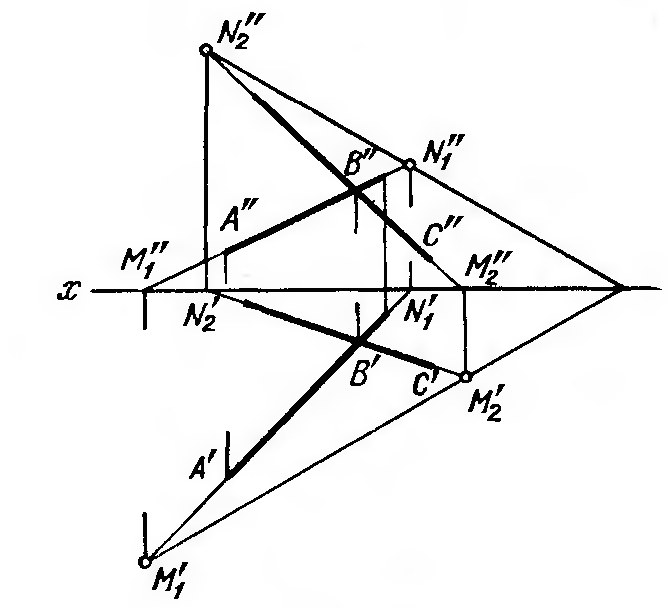
Кейде проекциялық жазықтықта жазықтықтың тек ізі берілуі мүмкін (суреттің оң жағы).

Еш проекциялық жазықтыққа перпендикуляр болмайтын жазықтықты ортақ жағдайдағы жазықтық деп атайды.

Горизонталь проекциялық жазықтыққа перпендикуляр жазықтықты горизонталь проекциялаушы жазықтық деп атайды.

Фронталь проекциялық жазықтыққа перпендикуляр жазықтықты фронталь проекциялаушы жазықтық деп атайды.

Профильді проекциялық жазықтыққа перпендикуляр жазықтықты профильді проекциялаушы жазықтық деп атайды.

Түзудің жазықтыққа қатысты орналасуы

Түзу жазықтыққа қатысты келесі түрде орналасуы мүмкін: жазықтық бойында жататын түзулер, жазықтыққа паралель, жазықтыққа перпендикуляр, түзу жазықтықпен қиылысады.

Жазықтықтың бойында жататын түзулер келесі түрлерге бөлінеді:

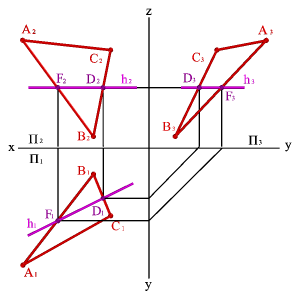
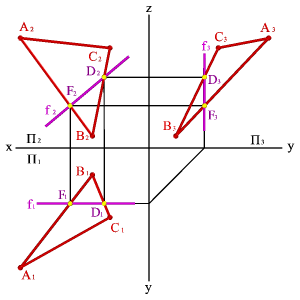
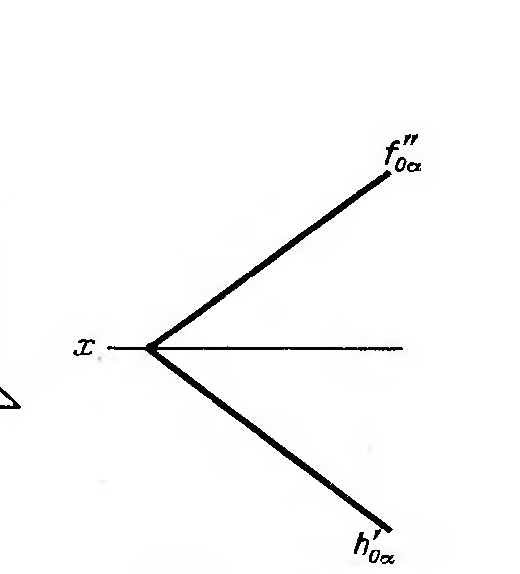
1. Горизонталдар – жазықтық бойында жататын және горизонталдық проекциялық жазықтыққа паралель жататын түзулерді айтады. (hÎABC, h//P₁, h₂//Ох,h₃//Оy). 

2. Фронталдар f – жазықтық бойында жататын және фронталь проекциялық жазықтығына паралель орналасқан түзулерді айтады. (fÎАВС, f//P₂, f₁//Ох, f₃//Оz).

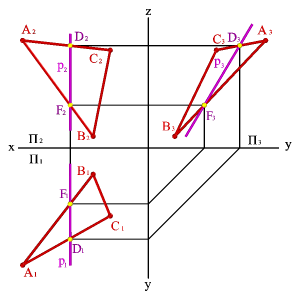
3. Профильдер р - жазықтық бойында жататын және профиль проекциялық жазықтығына паралель орналасқан түзулерді айтады (рÎABC, р//P₃, р₁^Ох, р₂^Ох)