21. Ортогоналдық проекцияларды түрлендіру әдістері.Проекция жазықтықтығына параллел өсі бойынша айналдыру әдісі

Жазықтыққа түсірілген нүктенің ортогональды проекциясы деп осы нүктеден жазықтыққа түсірілген перпендикулярдың негізі аталады.

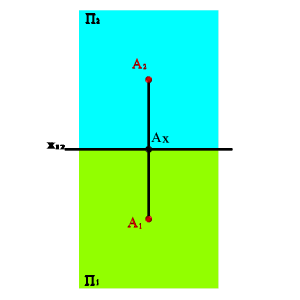
Суретте А нүктесі және оның А₁ және А₂ ортогональды проекциялары көрсетілген.

А₁ нүктенің горизонтальды проекциясы, ал А₂ – оның фронтальды проекциясы деп аталады. Нүктелердің проекциялары әрқашан х₁₂ осіне перпендикуляр түзудіің бойында орналасқан және осы осьті А_х нүктесінде қиып өтеді.

Егер проекция жазықтықтарында түзулердің бойында берілген және х₁₂ осін А_х нүктесін тік бұрышпен қиятын А₁ және А₂ нүктелері берілсе, онда олар қандай да бір А нүктесінің проекциясы деп аталады.

Нүкте – геометрияның негізгі түсініктерінің бірі. Математикада нүкте деп табиғаттың әртүрлі кеңістіктерінен тұратын элементтерін айтады (мысалы, n - өлшемді евклид кеңістігінде нүкте деп n - саннан тұратын жиынды айтады).

Проекцияларды тұрғызған кезде төмендегі мәселелерді есте сақтау қажет, жазықтыққа түсірілген нүктенің ортогональды проекциясы берілген нүктеден осы жазықтыққа түсірілген перпендикулярдың табаны деп аталады. 2.1. - Суретте А нүктесі және оның екі А₁ және А₂ ортогональды проекциялары көрсетілген.

А₁ нүктесін А нүктесінің горизонтальды проекциясы, А₂ нүктесін фронтальды проекциясы деп атайды. Нүкте проекциялары x₁₂ осіне перпендикуляр түзуде орналасқан және осы өсті А_x нүктесінде қиып өтеді.

2.1. - Сурет. Нүкте екі проекция жазықтықтарының ортогональды жүйесінде

Монж эпюрінде А₁ және А₂ проекциялары x₁₂ өсіне перпендикуляр түзуінде орналасқан. Нүктелердің горизонтальды проекцияларынан оске дейінгі А₁А_x – арақашықтығы А нүктесімен П₂ жазықтығына дейінгі қашықтыққа тең.

Эпюрде нүкте проекцияларын қосатын түзу сызықтар проекциялар байланысының сызығы деп аталады.

21.Проекциялар жазықтығына параллель өс бойынша

айналдыру әдісі

Бұл әдісті өзара қиылысушы түзулердің бұрышын анықтайтын мысалда қарастырайық (4.5. - сурет). К нүктесінде қиылысатын а мен в қиылысушы түзулерінің екі проекциясын қарастырамыз. Осы түзулердің арасындағы бұрыштың шынайы өлшемін анықтау үшін, түзулерді проекциялар жазықтығына параллель болатындай етіп түрлендіру қажет. Горизонталь деңгейлік түзу бойымен айналдыру әдісін қолданамыз. Кез-келген a және b түзулерін қиып өтетін Ох өсіне параллель h₂ горизонталін фронталь проекциясына жүргіземіз.

4.5. – Сурет. Горизонталь проекциялар жазықтығына параллель өс бойынша айналу арқылы қилысушы түзулердің арасындағы бұрыштарды анықтау

К₁ нүктесінің қозғалыс траекториясы К₁О₁ түзуімен анықталған, О нүктесі шеңбердің центрі. Шеңбердің радиусын анықтау үшін КО кесіндісінің шынайы өлшемін үшбұрыш әдісімен табамыз. К₁О₁ түзуін |КО|=|О₁К₁*| болғанша созамыз. Егер түзулері П₁ жазықтығына параллель жазықтықта жататын болса және горизонталь айналу өсі бойынша жүргізілген, онда К₁* нүктесі К нүктесіне сәйкес келеді. П₁ – ге параллель жазықтықта орналасқан К₁* нүктесі мен А₁, В₁ нүктелері арқылы түзулер жүргіземіз. Осы екі түзудің арасындағы бұрыш а мен в арасындағы бұрышының φ бұрышының шынайы мәні болады.