1. Инженерлік графика нені зерттейді және оның негізгі мақсаттары
Қазіргі кезде инженерлік графика пəні сызба геометрия пəні мен машина жасау жəне құрылыс сызбаларының теорияларын зерттейтін ғылым. Инженерлік графика теорияларының жетістіктері техника мен ғылымның əртүрлі салаларында кеңінен қолданылуда. Сондықтан жер жұмыстарының сызбаларын сауатты орындау, инженерлік ғимараттарды жобалау жəне тұрғызу үшін, жер бетінде салынатын ғимараттарды сызбада кескіндеу теориясының негіздерін инженер осы инженерлік графика теориясы арқылы біліп, үйренеді.
Сызықтық геометрия– кеңістіктегі фигуралар, олардың шешу әдістері және кеңістіктік есептерді жазықтықтағы суреттермен зерттейтін геометрияның бөлігі. Сызықты геометрияның әдістері техникалық сызудың теориялық базасы болып табылады. Бұл ғылымның мақсаты – машинасалу, архитектура және құрылыс объектілерінің пішінін салу, объектілер мен процестердің графикалық кескінін өңдеу.
Сызықтық геометрияды:
Кеңістіктегі фигураларды жазықтықта салудың әдістері;
Геометриялық есептердің графикалық және аналитикалық шешуінің әр түрлі әдістері;
Салынған объектінің геометриялық қасиеттерін зерттеу және түрлендіру әдістері;
Геометриялық объектілердің моделдеу зерттеледі
Сызу геометрияда салынған суреттер предметтердің ойдағы формасын елестетуге мүмкіндік беріп, кеңістіктік елестетуді дамытады. Сызу геометриядағы сызуларды салу әдісінің ережелері проекциялық әдіске негізделген. Проекциялық әдісте ең алдымен нүктенің проекциясын салу қарастырылады. Себебі кез келген кеңістіктік фигураларды салу осы фигура бойында жататын нүктелердің жиынтығы ретінде қарастырылады.
2. Монж әдісі ,Проекциялық жазықтықтар
Егер нүкте мен проекция жазықтығының арақашықтығы туралы ақпаратты сандық белгілеу көмегімен емес екінші проекциялар жазықтығында тұрғызылған нүктенің проекциясы арқылы берсе, онда сызба екі көріністі немесе кешенді деп аталады. Осындай сызбаның негізгі принциптерін француз ғалымы Гаспар Монж (1746-1818) келтірген.
|
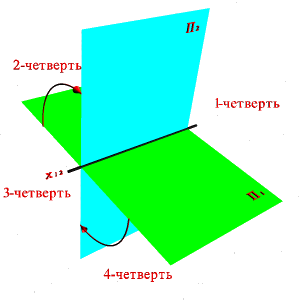
Г.Монждің ұсынған әдісі бойынша кеңістікте екі өзара перпендикуляр орналасқан проекция жазықтықтарын қарастырамыз. Жазықтықтардың біреуін П1 деп белгілейміз және горизонталь орналастырамыз, ал екінші П2 жазықтығын вертикальды орналастырамыз. П1 – горизонтальды, П2- фронтальды проекциялар жазықтығы. Проекция жазықтықтары кеңістікті төрт екі жақты бұрыштарға - төрт ширекті кеңістіктерге бөледі. |
1.6. - Сурет. Екі проекциялар жазықтықтарының кеңістіктік моделі |
Ортогональды проекцияларға байланысты, проекция жазықтықтарынан бақылаушы шексіз үлкен қашықтықта бірінші ширекте тұр деп есептейміз. Проекция жазытықтарының қиылысу түзуі координатлар өсі деп аталады x12 немесе x болып белгіленеді. Көрсетілген проекциялардан тұратын жазық сызба алу үшін П1 жазықтығын x12 өсімен айналдыру арқылы П2 жазықтығымен беттестіреміз. Нәтижесінде алынған сызба Монж Эпюрі деп аталады. Геометриялық объектілер сызықты (нүкте, түзу, жазықтық), сызықты емес (қисық сызық, бет) және құраушы (көпжақтар) болып бөлінеді. Монж ұcынған тәсіл. Есiмi тарих бетiнде қалған Госпар Монж (1746-1818) көрнектi француз геометрi, XVII ғасыр аяғында және Напалеон I басшылық еткен 1789-1794 жылдар аралығындағы қоғамдық және мемлекеттiк қайраткер. Париждегi белгiлi Политехникалық мектептiң негiзiн қалаушы. Өлшем мен салмақтың метрлiк жүйесiн енгізу жұмысын жүргiзуге қатысқан. Франциядағы революция кезiнде министрлiк қызмет атқарған.
Монж әдiсiнiң үлкен құпия мәнi болғандықтан, еңбегiн жариялауға тиым салынады. Тек XVIII ғасырдың аяғында ғана басылуға мүмкіндік берiлдi.
Кеңiстiктегi пiшiндi жазықтықта бейнелеу қажеттiгi ежелгi заманнан берi жинақталып келдi. Техниканың дамуына байланысты алғашқы мәнi өлшеуге жеңiл нақты бейнелермен қамтамасыз ететiн қандайда бiр тәciлдiң
қажеттiгiн туғызады. Ол нүктенiң бейнедегi басқа үктелерге қарағанда орнын дәл анықтау, фигуралар мен түзукесiндiлерiнiң өлшемдерiн табу мүмкiндiгiнiң жеңiл жолдары. Француз ғалымы Монж бiртiндеп жинаған
әртүрлi ережелермен бейнелердi салу тәсiлдерiн бiр жүйеге келтiрiп, 1799 жылы «Geometrie dtscrihtive» деп аталатын еңбегiн басып шығарады.
Ортогональды проекцияда кеңicтiктегi геометриялық
фигуралардың пiшiнi мен орнын анықтауға ең қолайлысы өзара перпендикуляр болатын үш жазықтықтан тұратын декартты жүйе болып табылады. Геометриялық фигуралардың ортогональды проекцияларын салғанда
кеңicтiктегi макеттi қолдану өте ынғайсыз, көрнектi емес. Сондықтан бейне ретiнде сызбада кеңicтiктегi макеттiн орнына - эпюр сызбасы қолданылады, ол екi немесе үш өзара байланысқан геометриялық фигуралардың
ортогональды проекцияларынан тұрады. Монж көрнектi түрде проекция жазықтықтарын, олардың жалпы
жазықтықта беттесетiндей етiп қиылысу сызығымен қалай айналдыру керектiгiн көрcеттi. Бұнда ол бейнеленетiн заттың өзiн алып тастап, тек оның бейнелерiн, яғни проекцияларын қалдырған. Бұндай сызу комплекстi немесе Монж эпюрi деп аталады
Проекциялық жазықтықтар
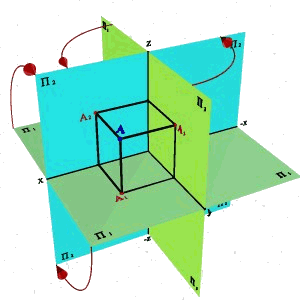
Бұл жазықтықтағы нүктелердің проекциялары үлкен әріптермен немесе 3 индексті сандармен белгіленеді.
Проекциялар жазықтығы жұп-жұбымен қиылысып Ox, Oy және Oz үш өсін анықтайды. Оны кеңістіктегі О нүктесімен басталатын декарттық координаттар жүйесінде қарастыруға болады. Үш проекциялар жазықтығында нүктенің эпюрін салу үшін П1 және П3 проекциялар жазықтықтарын 2.4. - суреттегідей П2 жазықтына айналдыру арқылы беттестіреміз. Кеңістіктегі немесе беттегі нүктенің орналасу жағдайын анықтау үшін сандардан тұратын координаттарды береміз. Үш өлшемді кеңістікте нүктенің орналасу жағдайын тік бұрышты декарттық координаттар x , y және z көмегімен анықтайды (абсцисса, ордината және аппликата).
Егер нүкте жазықтықтардың біреуінде жататын болса, проекциялар жазықтығына қарағанда нүкте жеке жағдайдағы нүкте деп аталады. Егер нүкте ешқандай жазықтықта жатпайтын болса, онда нүкте жалпы жағдайдағы нүкте деп аталады.