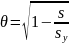37. Початковий змішаний момент

Аналогічно тому, як паралельно дисперсії (центральний другий момент) існує другий початковий момент, так і паралельно кореляційному (центральний змішаний момент) існує початковий змішаний момент:

M[xy]=Mx*My=β₁₁ – початковий змішаний момент

Зв’язок між центральним змішаним моментом і початковим змішаним моментом:

K_xy=M[(x-m_x)(y-m_y)]=M[xy-m_xy-xm_y+m_xm_y]=M[xy]-m_xM[y]- M[x]m_y+m_ym_x=β₁₁[xy]-m_ym_x

K_xy= β₁₁[xy]- m_ym_x

На практиці замість β₁₁[xy] використовують статистичний аналог початкового змішаного моменту:

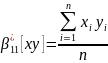
38. Статистичний аналог центрального змішаного моменту.

На практиці замість К_xy використовують статистичний аналог центрального змішаного моменту:

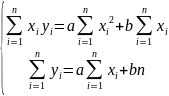
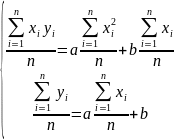
Зробимо відповідні заміни: ; ; ;

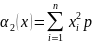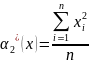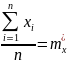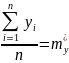
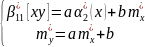
Замість початкових моментів 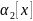та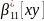 вводимо центральні 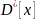та і розвяжемо систему

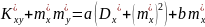
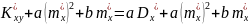
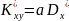
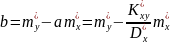
39. Рівняння регресії.

Використовуючи статистичні аналоги центрального та початкового змішаного моментів - та , перетворимо рівняння, отримані за методом найменших квадратів для лінійної залежності.

За формулою 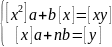маємо:

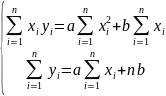
Розділимо обидві частини на n:

Зробимо відповідні заміни:

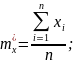
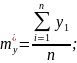
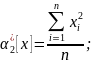
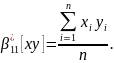
та отримаємо:

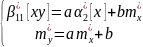
Замість початкових моментів 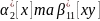вводимо центральні .

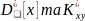Розв’яжемо цю систему:

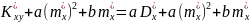
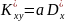
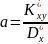
та

Розглянемо рівняння :

;

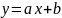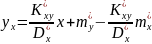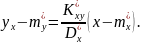
Саме останнє рівняння є прямою, яка проходить через точку (M) з координатами 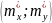та має тангенс кута нахилу 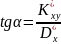і саме це рівняння називається рівнянням регресії y за x. Рівняння регресії отримано, виходячи з умови, що всі помилки включені у величину у, а величина х визначена точно.

Якщо y та x пов’язані функціональною залежністю, то функцію та аргумент можна змінювати місцями, тобто можна записати:

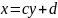
Коефіцієнти c та d однозначно пов’язані з коефіцієнтами а та b залежності при відсутності помилки експерименту. При наявності помилок параметри c та d знаходяться із умови: 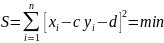, тобто зараз припускаємо, що всі помилки зосереджені в x . Мінімізуючи S за c та d і розв’язуючи відповідну систему лінійних рівнянь, отримуємо рівняння регресії x за y: 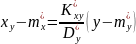Це рівняння відповідає прямій, що проходить також, як рівняння регресії y по x , через точку ( M ) з координатами та має котангенс кута нахилу 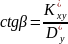, відповідно,

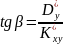
Рівняння регресії приймає більш простий вигляд у координатах:

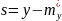та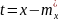 , тобто в системі координат, де початку координат відповідає точка M .

Перенесення початку координат не впливає на центральні, початкові змішані моменти, тому в координатах s-t рівняння регресії має вигляд:

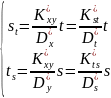
Ці рівняння використовуються для знаходження меж коефіцієнта кореляції.

40. Коефіцієнт кореляції.

Величина K_xy= М [(x-m_x)(y- m_y)] - центральний змішаний момент, що має назву кореляційний момент.

Кореляційний момент К_xy має розмірність, яка дорівнює розмірності добутку випадкових величин x та y. Зручніше користуватися безрозмірною величиною, коефіцієнтом кореляції (r): 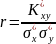Для незалежних величин x та y K_xy=0 та відповідно, r=0.

Знайдемо чому дорівнює величина r для жорсткої функціональної залежності за відсутності помилок експерименту. У цьому випадку всі точки ідеально лягають на пряму лінію і прямі регресії повинні тотожно співпасти.

S=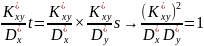

Добудемо квадратний корінь з обох частин рівняння та отримуємо:

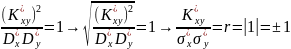
тобто точній функціональній залежності відповідає значення r = ± 1. У загальному вигляді: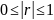

Наближення r до одиниці відповідає функціональній залежності; нулю - відсутності лінійної залежності; проміжне значення r вказує на наявність кореляційної залежності.

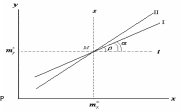
Коефіцієнту кореляції r можна дати графічну інтерпретацію:

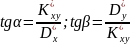
Відповідно:

тобто, чим більше розходиться між собою рівняння регресії, тим менший коефіцієнт кореляції.

Визначимо коефіцієнт кореляції аналітичним методом:

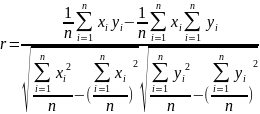
Для нелінійної залежності коефіцієнт кореляції не розраховується, а розраховується кореляційне відношення: