Статистичні методи в хімії fin

28. Нев’язка. Основне рівняння методу найменших квадратів.

Для двох величин (у та х),що зв’язані між собою функціональною залежністю: y_i = (a, b, c…x_i), кількість точок, яка необхідна для визначення параметрів, повинна бути не менша за число параметрів.

y=ax+b  >2 точки тощо (це справедливо за відсутності помилок експерименту)

Наявність випадкових помилок змінює ситуацію. Точки 1,2,3,4-відповідають лінійній залежності. Спроби вивести пряму лінію через довільну пару точок дає «віяло», що зображено на рис 4.1. Неспроможність подібних спроб є наявною. Це доводить, що використання всього двох точок для визначення прямої лінії при наявності випадкових помилок експерименту явно недостатньо, щоб отримати надійний несуперечливий результат.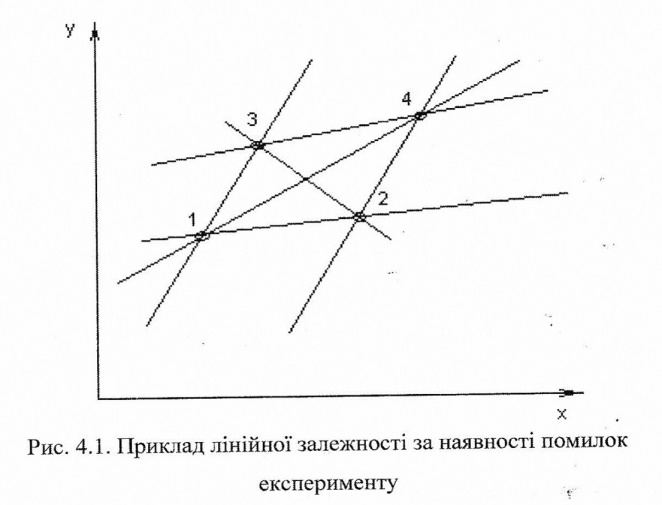

Таким чином, вплив випадкового фактору призводить до того що для надійного визначення параметрів масив експериментальних даних повинен бути істотно більшим за к-сть параметрів.

Подібний масив точок. (рис4.2)

З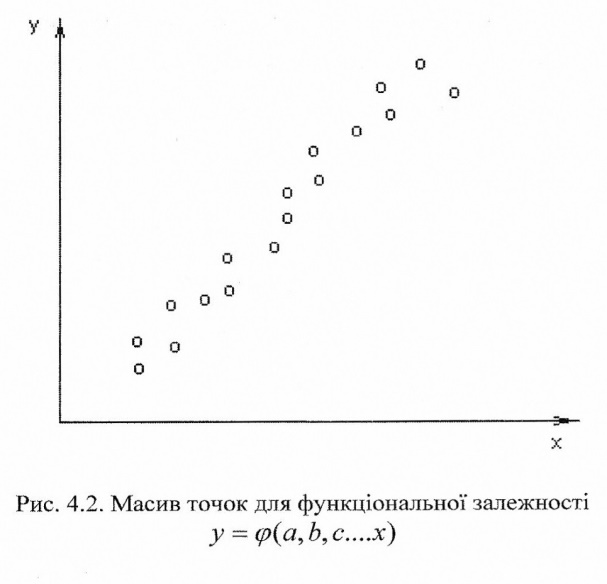 а умови заданості функціональної залежності задача полягає в оптимальному виборі параметрів (a,b,c…).Дії випадкових факторів, що зумовлюють розкид точок, підлягають як функція (у), так і аргумент (х),але можна зосередити усі помилки на функції (у) і вважати ,що аргумент (х) визначений вірно. 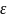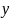Відхилення функції (y_i )від її точного значення-математичного сподівання (m[y_i ]) позначимо через ₁ і назвемо нев’язками: ₁ = ₁ – m [ ₁]

m [ ₁ ] = (a, b, c…x_i)

₁ = ₁ -(a, b, c…x_i)

Вважаємо, що закон розподілення випадкової величини є нормальним

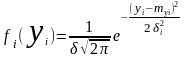
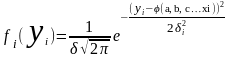
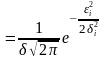
Згідно з теореми множення ,ймовірності появи n точок. Закон розподілу величину повинен бути нормальним

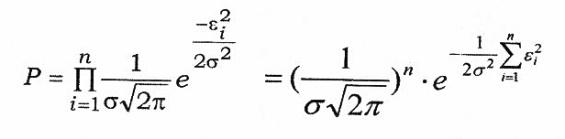
Ймовірність того,що ці зн. найбільш близькі до своїх точних значень,максимальна тоді,коли 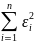=min

Це і є основне рівняння МНК

Застосування МНК для залежностей y=ax та y=ax+b

Щоб знайти мінімальне значення =S знаходимо екстремум,для цього знаходимо похідну і прирівр.но 0.

y=ax

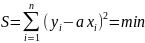
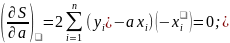
[xy]=a[x² ]

a=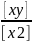

29. Застосування методу найменших квадратів для залежностей: y=ax; y=ax+b.

Щоб знайти мінімальне значення =S знаходимо екстремум, для цього знаходимо похідну і прирівнюємо до 0.

y=ax

[xy]=a[x² ]

a=

2. y=ax+b

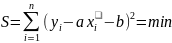Для трьох параметрів (c, b, a) знаходимо три рівняння:

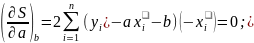
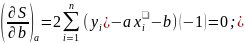
-[xy]+a[x²]+b[x]=0

-[y]+a[x]+bn=0

;

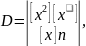
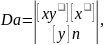
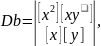
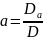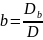
30. Лінеаризація.

Відносна простота та зручність обробки лінійної залежності методом найменших квадратів підказує зручний спосіб обробки нелінійних залежностей – попередня їх лінеаризація. Лінеаризація можлива, якщо числа параметрів не перевищує двох. Можливість лінеаризації не завжди вдається перетворити в дійсність, наприклад функція y=b₀ + e^b1x не лінеаризується. Конкретний приклад обробки з використанням лінеаризації розглянуто нижче.

Рівняння реакції І порядку: С = С₀е^-к,т , після лінеаризації ln C = lnC₀ – K₁t y = ax + b y = lnC a = -K₁ b = lnC₀ x = t

Рівняння реакції ІІ порядку:

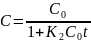
Після лінеаризації y = ; a = K₂;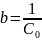 ; x = t;

Рівняння Арреніуса: K = K₀

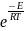
Після лінеаризації: lnK = lnK₀ -

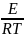
Х = 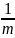; y = lnK; b = lnK₀; a =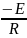

31. Застосування методу найменших квадратів для залежності y=ax²+bx+c.

Рівняння параболи має три параметри: a, b, c: y=ax²+bx+c. Для суми квадратів невязок у випадку параболічної залежності отримуємо:

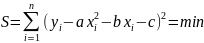Для трьох параметрів (c, b, a) знаходимо три рівняння:

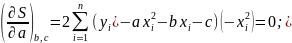
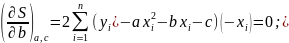
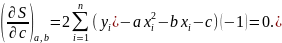
Нескладні перетворення з введенням позначок Гаусса дають:

; ,

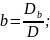
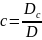де

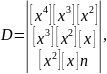
а детермінанти D_c, D_b і D_a отримуються із D шляхом заміни відповідного стовпчика на стовпчик 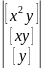вільних членів.