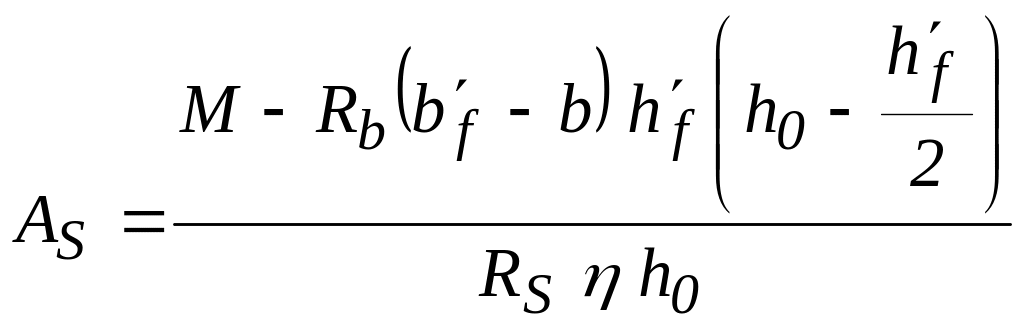2.4.2 Розрахунок міцності нормальних перерізів

Оскільки другорядна балка, як і плита , є частиною монолітного перекриття, то переріз другорядної балки має таврову форму. Розрахунковий переріз балки – тавр з полицею угорі. Коли розтягнення відбувається внизу, то полиця знаходиться у стиснутій зоні. ЇЇ треба враховувати на ширині не більше, ніж

при hf’/h  0,1	1) 2)		(2.68)
при hf’/h  0,1	1) 2)

де – ширина стиснутої полиці;

– висота перерізу другорядної балки ;

– товщина стиснутої полиці, дорівнює висоті монолітної плити ;

– ширина ребра другорядної балки ;

– крок другорядних балок;

– проліт другорядних балок.

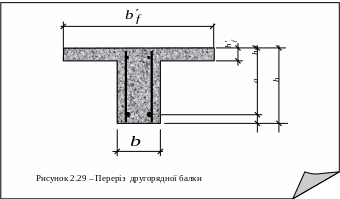
По довжині балки виникають додатні і відємні моменти. Це означає, що стиснута зона міняє положення. При виникненні додатніх моментів стиснутою є верхня зона, де знаходиться полиця. Розрахунок таких перерізів починають із визначення, де знаходиться нейтральна вісь від дії найбільшого додатнього моменту М₁ :

М  Мf’ = Rb × bf’ × hf’ × (h0 – 0,5 hf'),

(2.69)

де в лівій частині нерівності момент від навантаження М = М₁ × 10⁵ (Нсм);

М_f^’ – момент, який може сприймати переріз при умові повністю стиснутої полиці, тобто при ;

– розрахунковий опір бетону з урахуванням коефіцієнту ;

– найменша ширина стиснутої полиці, що враховується в розрахунках;

– висота стиснутої полиці;

– робоча висота перерізу, її визначають за формулою (2.30) і згідно з пунктом 2.3.2.

Якщо умова (2.69) виконується, то нейтральна вісь знаходиться у полиці, до розрахунків приймаємо прямокутний переріз завширшки b_f^’. Подальші розрахунки перерізів на дію додатніх моментів виконують за формулами (2.33)÷(2.36) при .

Якщо умова (2.69) не виконується, то нейтральна вісь знаходиться у ребрі, до розрахунків приймаємо тавровий переріз. Подальші розрахунки перерізів на дію додатніх моментів таврової форми виконують за наступним алгоритмом.

• Знаходять коефіцієнт А₀

  .

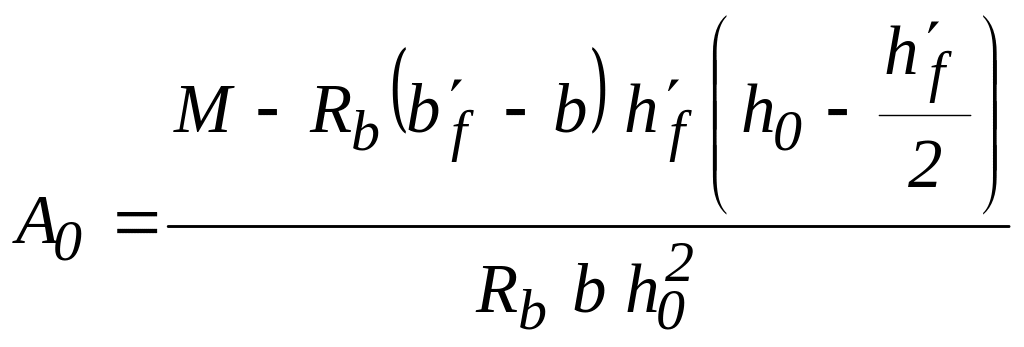  (2.70)

• Далі із таблиць або за формулами (2.34) і (2.35) знаходять допоміжні коефіцієнти  і , порівнюють відносну висоту стиснутої зони з її граничним значенням. Якщо    _R , то стиснута арматура з розрахунку не потрібна, площу потрібної робочої розтягнутої арматури визначають за формулою:

(2.71)

Всі позначення у формулах (2.70) і (2.71) такі ж як і в попередніх формулах.

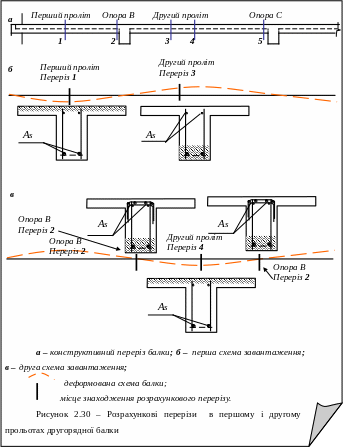
У місцях, де діють відємні моменти, стиснута зона знаходиться внизу, тому до розрахунків приймають ширину перерізу b = Bsb у формулах (2.33)÷(2.36).

Перерізи, які потрібно розрахувати, на рисунку 2.30 позначені цифрами 1,2,3,4,5.

Приклад 7

Розрахувати нормальні перерізи другорядної балки.

Вихідні дані: епюра моментів із прикладу 6, а розміри перерізу другорядної балки – із прикладу 2.

• Висота перерізу плити = 6 см;

• Висота перерізу другорядної балки = 40 см;

• Ширина перерізу другорядної балки = 15 см;

• Ширина перерізу головної балки = 200 мм;

• Проліт другорядної балки в осях 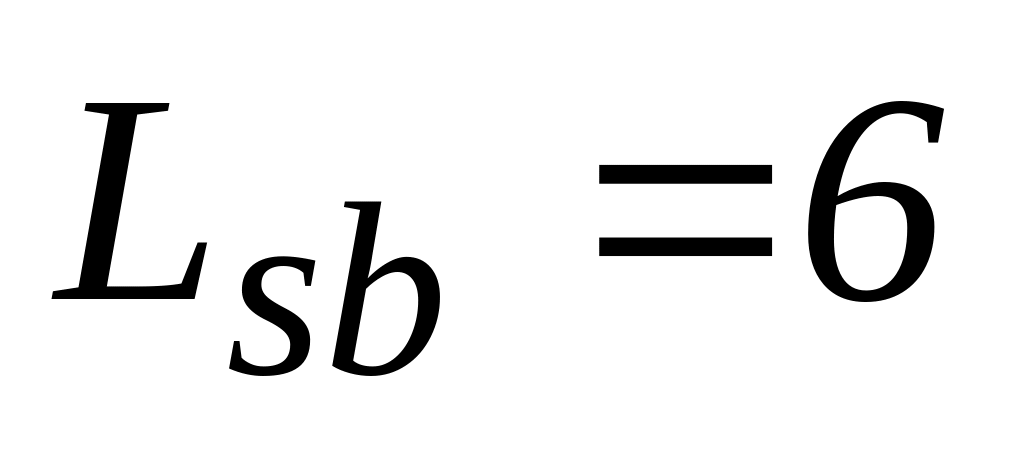м;

• Крок другорядних балок 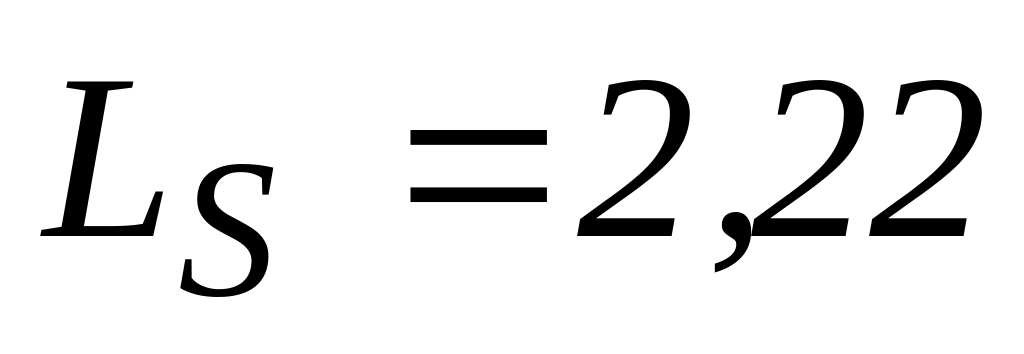м;

• Розрахунковий опір бетону стиску при класі бетону В = 15 = 8,5 МПа;

• Робоча арматура класу А ІІІ при Æ 10 і більше = 365 МПа, і при Æ 6 і при Æ 8 – = 355 МПа;

• При класі бетону В 15, арматурі класу А ІІІ і .

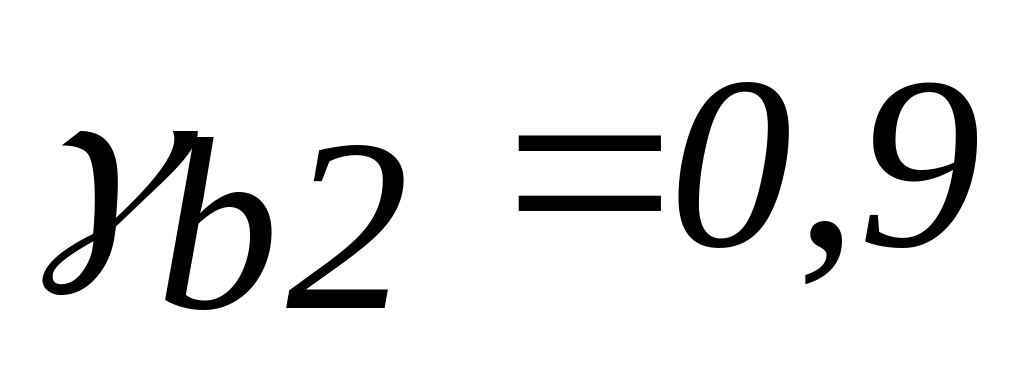
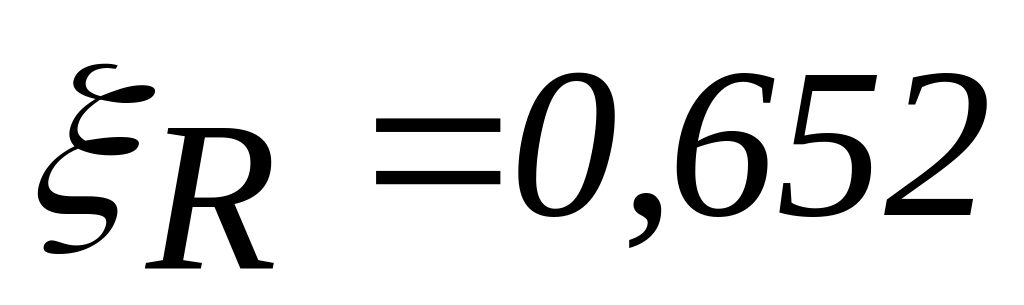• Значення згинальних моментів:

  • перший проліт, розтягнення внизу – = 50,5 кНм,

  • опора В, розтягнення вгорі – = —39,7 кНм,

  • другий проліт, розтягнення вгорі – 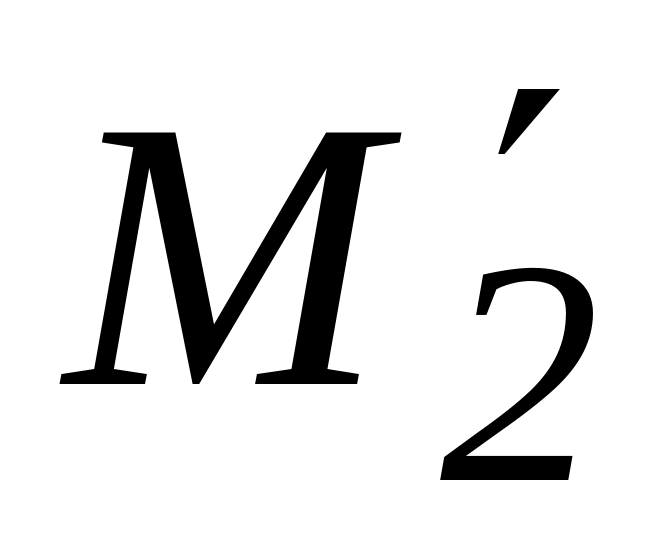 = —2,97 кНм,

  • другий проліт, розтягнення внизу – = 34,4 кНм,

  • опора С, розтягнення вгорі – = —34,4 кНм.

Геометрія перерізів балки.