
- •2.4 Розрахунок і конструювання другорядної балки
- •2.4.1 Розрахункова схема та зусилля
- •Приклад 6
- •2.4.2 Розрахунок міцності нормальних перерізів
- •Приклад 7
- •Висота перерізу см, робоча висота см.
- •2.4.3 Розрахунок похилих перерізів
- •2.4.3.2 Розрахунок похилих перерізів на дію поперечної сили
- •2.4.3.3 Перевірка міцності стиснутої смуги
- •Приклад 8
- •2.4.4 Конструювання другорядної балки
2.4 Розрахунок і конструювання другорядної балки
2.4.1 Розрахункова схема та зусилля
Для складання розрахункової схеми
подумки вирізаємо смугу завширшки LS
вздовж
другорядної балки (див. рис. 2.22). Одна
балка тягнеться від стіни до стіни.
Спирання на стіни вважається умовно
шарнірним. Із головними балками
перетинання монолітне, тобто жорстке
(на схемі позначається як шарнір. який
не розрізає балку). Кількість прольотів
другорядної балки
![]() .
Розрахункова схема другорядної балки
– це багатопролітна нерозрізна балка
(рис. 2.23), завантажена рівномірно-розподіленим
навантаженням (у межах прольоту). Для
середніх прольотів
приймають рівними відстані між
прогонами (головними балками) у світлі,
для крайніх прольотів при обпиранні
балок на стіну – відстані від бічної
поверхні головної балки до центру опори
на стіні, для крайніх прольотів при
наявності по контуру перекриття
обв'язувальних балок – відстані у світлі
між прогоном обв'язувальною балкою.
.
Розрахункова схема другорядної балки
– це багатопролітна нерозрізна балка
(рис. 2.23), завантажена рівномірно-розподіленим
навантаженням (у межах прольоту). Для
середніх прольотів
приймають рівними відстані між
прогонами (головними балками) у світлі,
для крайніх прольотів при обпиранні
балок на стіну – відстані від бічної
поверхні головної балки до центру опори
на стіні, для крайніх прольотів при
наявності по контуру перекриття
обв'язувальних балок – відстані у світлі
між прогоном обв'язувальною балкою.

Розрахункові прольоти визначають за наступними формулами:
|
(2.53) |
|
(2.54) |
де
![]() – крайній розрахунковий проліт, це
відстань від грані головної балки до
середини спирання другорядної балки
на стіну, мм;
– крайній розрахунковий проліт, це
відстань від грані головної балки до
середини спирання другорядної балки
на стіну, мм;
![]() – середні розрахункові
прольоти, це відстань між головними
балками;
– середні розрахункові
прольоти, це відстань між головними
балками;
![]() – довжина спирання балки на
стіну, дорівнює 250 мм,
тобто стандартний розмір цеглини;
– довжина спирання балки на
стіну, дорівнює 250 мм,
тобто стандартний розмір цеглини;
Пр – прив’язка стіни 200 мм;
![]() – ширина перерізу
другорядної балки, мм.
– ширина перерізу
другорядної балки, мм.
Вантажна смуга для збору навантаження на одну балку має ширину, що рівна кроку другорядних балок: bвант = LS .
Розрахункове навантаження, розподілене на погонний метр, визначається за наступними формулами:
|
(2.55) |
|
(2.56) |
|
(2.57) |
|
(2.58) |
|
(2.59) |
|
(2.60) |
де
![]() – постійне розрахункове
погонне навантаження, кН
/ м;
– постійне розрахункове
погонне навантаження, кН
/ м;
![]() – постійне погонне
навантаження від ваги
монолітної плити і підлоги, визначається
за формулою (2.56);
– постійне погонне
навантаження від ваги
монолітної плити і підлоги, визначається
за формулою (2.56);
![]() – постійне погонне
навантаження від ваги
другорядної балки, визначається за
формулою (2.57);
– постійне погонне
навантаження від ваги
другорядної балки, визначається за
формулою (2.57);
![]() – постійне розрахункове
навантаження, кН / м2,
із таблиці збору навантаження на 1 метр
квадратний перекриття;
– постійне розрахункове
навантаження, кН / м2,
із таблиці збору навантаження на 1 метр
квадратний перекриття;
![]() – ширина вантажної смуги
(рис. 2.22), чисельно дорівнює кроку
другорядних балок,
– ширина вантажної смуги
(рис. 2.22), чисельно дорівнює кроку
другорядних балок,
![]() ,
м;
,
м;
![]() – коефіцієнт надійності
будівлі, визначається за класом (І клас
– 1, ІІ клас – 0,95, ІІІ клас – 0,9);
– коефіцієнт надійності
будівлі, визначається за класом (І клас
– 1, ІІ клас – 0,95, ІІІ клас – 0,9);
![]() – коефіцієнт надійності з
навантаження, для конструкцій з важкого
бетону
– коефіцієнт надійності з
навантаження, для конструкцій з важкого
бетону
![]() ;
;
![]() – щільність важкого бетону,
25 кН
/ м3;
– щільність важкого бетону,
25 кН
/ м3;
![]() – площа перерізу другорядної
балки, м2
– площа перерізу другорядної
балки, м2
![]() – тимчасове погонне
навантаження, кН / м;
– тимчасове погонне
навантаження, кН / м;
![]() – тимчасове розрахункове
навантаження, кН / м2,
із таблиці збору навантаження на 1 метр
квадратний перекриття;
– тимчасове розрахункове
навантаження, кН / м2,
із таблиці збору навантаження на 1 метр
квадратний перекриття;
![]() – повне погонне
навантаження, кН / м;
– повне погонне
навантаження, кН / м;
![]() – висота перерізу другорядної
балки, м;
– висота перерізу другорядної
балки, м;
![]() – висота перерізу плити,
м;
– висота перерізу плити,
м;
![]() – ширина перерізу другорядної
балки, м.
– ширина перерізу другорядної
балки, м.
Досвід проектування дозволяє конкретизувати приведені загальні рекомендації стосовно до розрахунку рівнопролітних нерозрізних другорядних балок, а також другорядних балок, прольоти яких відрізняються не більш ніж на 10%.
Згинальні моменти в рівнопролітних другорядних балках, завантажених рівномірно розподіленим навантаженням, рекомендується визначати за формулами:
|
(2.61) |
|
(2.62) |
|
(2.63) |
де
![]() – опорні моменти на середніх опорах
кНм;
– опорні моменти на середніх опорах
кНм;
![]() – пролітні моменти в середніх
і крайніх прольотах,
кНм;
– пролітні моменти в середніх
і крайніх прольотах,
кНм;
![]() –
опорні моменти на других від
кінця опорах (над першою від стіни
головною балкою), кНм;
–
опорні моменти на других від
кінця опорах (над першою від стіни
головною балкою), кНм;
– повне розрахункове навантаження (формула (2.55));
![]() – розрахункові прольоти
(формули (2.23), (2.54)).
– розрахункові прольоти
(формули (2.23), (2.54)).
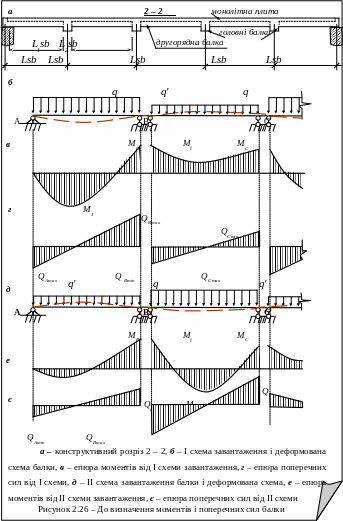
При проектуванні нерозрізних балок враховують можливість нерівномірного навантаження, для чого будують обвідну епюру моментів від двох схем завантаження:
в першому, третьому, п’ятому прольотах – повне навантаження , в інших прольотах прикладають приведене навантаження
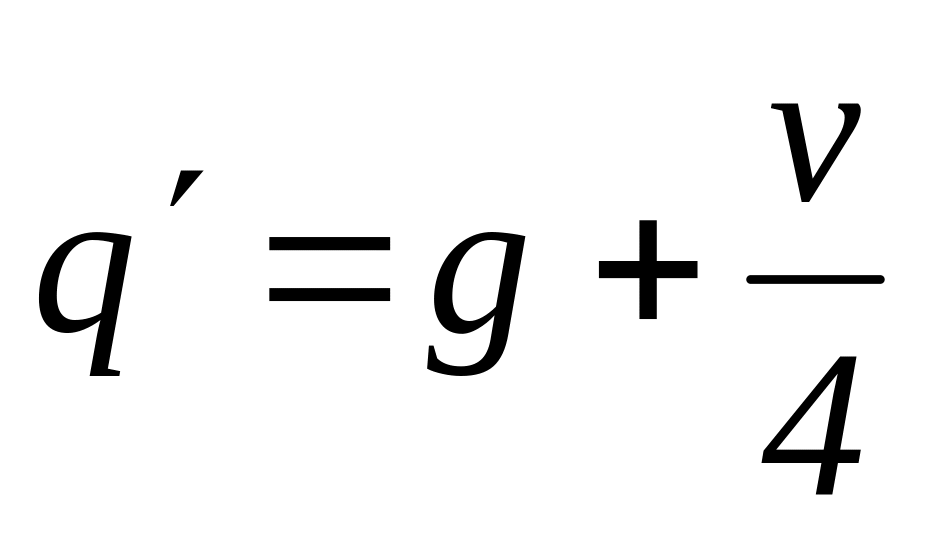 ;
;в першому, третьому, п’ятому прольотах прикладають приведене навантаження
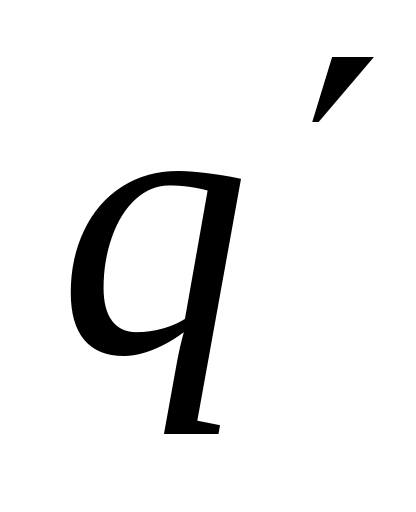 ,
другому, четвертому прольотах – повне
навантаження
.
,
другому, четвертому прольотах – повне
навантаження
.
Епюри згинальних моментів, що обгинають найбільші значення, для другорядних рівнопролітних нерозрізних балок будують у такий спосіб:
Мінімальні моменти – у всіх середніх прольотах по параболах, що відповідає дії приведеного постійного тимчасового навантаження. Ця парабола проходе через вершини розрахункових опорних ординат. В крайніх прольотах – по прямих, яку будують за двома точками: максимальною опорною ординатою і нульовою точкою, що знаходиться від опори В на відстані
 ;
;Максимальні моменти – по параболах, що відповідає дії повного навантаження, із вершинами на максимальних ординатах прольотних моментів, а саме: у крайніх прольотах відкладають
 на
відстані
на
відстані
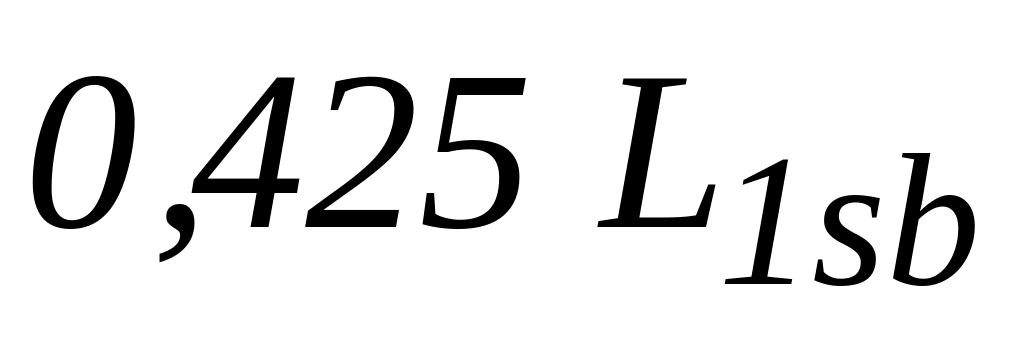 від
вільного кінця, а в інших прольотах –
посередині прольотів відкладають
від
вільного кінця, а в інших прольотах –
посередині прольотів відкладають
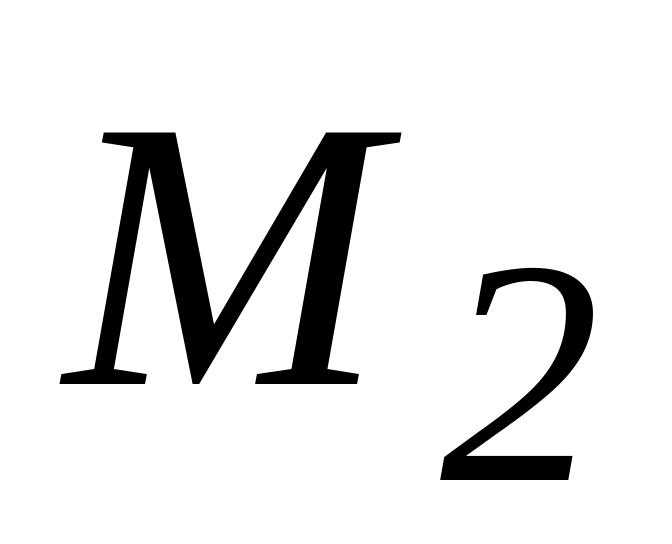 .
.
Ординати епюр згинальних моментів
для рівнопролітних другорядних балок
при співвідношеннях тимчасового
навантаження до постійного навантаження
![]() ,
визначають за формулою (2.64) для кожної
точки і
,
визначають за формулою (2.64) для кожної
точки і
|
(2.64) |
де β – коефіцієнт, що залежить від відношення навантаження v / g, значення його визначають за допомогою таблиць (додаток В) для точки і;
– повне розрахункове погонне навантаження, кН / м;
![]() – розрахунковий проліт,
крайній або середній, відповідно для
точки і;
– розрахунковий проліт,
крайній або середній, відповідно для
точки і;
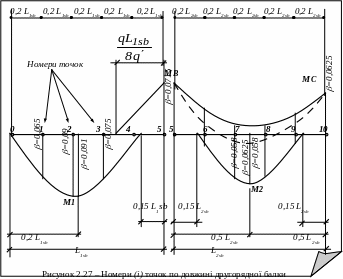
![]() – номер точки по довжині
балки (див. рис. 2.27).
– номер точки по довжині
балки (див. рис. 2.27).
Поперечні сили для рівнопролітних другорядних балок визначають за формулами (позначення в наступних формулах такі самі, як і в попередніх):
|
(2.65) |
|
(2.66) |
|
(2.67) |
де
![]() – поперечна сила на опорі А (шарнір при
спиранні балки на стіну);
– поперечна сила на опорі А (шарнір при
спиранні балки на стіну);
![]() – поперечна сила у першому
прольоті на опорі В (нерозрізне спирання
другорядної балки на головну);
– поперечна сила у першому
прольоті на опорі В (нерозрізне спирання
другорядної балки на головну);
![]() – те саме, у другому прольоті;
– те саме, у другому прольоті;
![]() – поперечна сила у другому
прольоті на опорі С;
– поперечна сила у другому
прольоті на опорі С;
 – повне розрахункове
навантаження,
– повне розрахункове
навантаження,
![]() ;
;
![]()
 – розрахункові прольоти
другорядної балки, (форм. (2.53), (2.54)).
– розрахункові прольоти
другорядної балки, (форм. (2.53), (2.54)).
