
- •Физика в задачах Механика
- •Предисловие
- •1. Кинематика Основные понятия, соотношения, формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •2. Динамика Основные понятия, соотношения, законы
- •Примеры решения задач (Поступательное движение твердого тела)
- •Задачи для самостоятельного решения (Поступательное движение твердого тела)
- •3.Законы сохранения Примеры решения задач
- •Задачи для самостоятельного решения (Законы сохранения)
Задачи для самостоятельного решения (Законы сохранения)
Небольшое тело массой m1=10г налетает на неподвижный шар массой m2=50г. Направление движения тела составляет угол α=450 с нормалью к поверхности шара в точке столкновения. Считая столкновение абсолютно упругим, определите, под каким углом к этой нормали отскакивает тело после столкновения (β=560).
Шар, движущийся со скоростью u0=10м/с, сталкивается с неподвижным шаром, радиус которого в k=R/r=2 раза больше радиуса налетающего шара. Найти скорости шаров после упругого столкновения, если прицельное расстояние равно p=0,4(R+r). Шары изготовлены из одного материала. Чему равен угол разлёта шаров? (2,0м/с; 8,2м/с; 770).
Два тела массой m1=1,0кг и m2=3,0кг движутся навстречу друг другу во взаимно перпендикулярных направлениях со скоростями u1=3,0м/с и u2=1,0м/с. В результате столкновения тела слипаются. Определите количество теплоты, которое выделяется в результате столкновения (3,8Дж).
Пуля массой m=9,0г, летящая со скоростью u0=500м/с, пробивает брусок массой М=1,8кг, лежащий на гладкой горизонтальной поверхности, и вылетает со скоростью u=50м/с. Определите скорость бруска и теплоту, которая выделяется при этом столкновении (2,3м/с; 1,1кДж).
Шайба ударяется о горизонтальную поверхность льда под углом α=300. Коэффициент трения скольжения шайбы о лёд μ=0,17. Определите относительную долю кинетической энергии шайбы, которая при ударе превращается в теплоту. Под каким углом b(град) к горизонту отскакивает шайба? Действием силы тяжести в процессе столкновения пренебречь, движение шайбы считать поступательным (0,27; 360).
Хоккейная шайба налетает на борт под углом α=310 к нормали. Коэффициент трения между шайбой и бортом μ=0,21. Определите, под каким углом к нормали отражается шайба от борта (100).
Небольшое тело массой m=54г, движущееся горизонтально со скоростью u0=25м/с, сталкивается с неподвижным гладким клином массой м=140г. Угол наклона клина к горизонту равен α=300. Клин может без трения скользить по горизонтальной поверхности. Определите скорость движения клина после столкновения (4,4м/с).
По гладкой горизонтальной поверхности движется тело массой m=2,1кг со скоростью u0=5,3м/с и упруго сталкивается с неподвижным телом массой м=6,8кг. Определите скорости тел после столкновения (-2,8м/с; 2,5м/с).
Гимнаст падает с высоты h=4,2м на упругую сетку (батут). Во сколько раз максимальная сила упругости сетки больше силы тяжести гимнаста, если под действием силы тяжести гимнаста сетка прогибается на величину S=21см (7,4).
На пружину длиной l=5,3см, закрепленную на горизонтальной поверхности, падает тело с некоторой высоты массой m=1,7кг. На каком расстоянии от поверхности скорость тела будет максимальной, если жесткость пружины равна k=12Н/см (3,9см).
По горизонтальной поверхности скользит без трения “горка” высотой h=1,2м и массой М=0,5кг. При какой наименьшей скорости “горки” небольшое тело массой m=0,1кг, неподвижно лежащее на её пути, перевалит через вершину (3,8м/с).
Человек стоит на неподвижном плоту. Сделав 8 шагов вдоль плота, человек остановился. На сколько “шагов” при этом передвинется плот? Масса плота в три раза больше массы человека (2).
Альфа-частица с кинетической энергией Кα=4,0МэВ упруго рассеивается на покоящемся протоне. Определите кинетическую энергию частиц после рассеяния. Столкновение считать центральным (
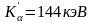 ,
,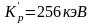 ).
).На мишень из трития падают дейтоны с кинетической энергией 2,0МэВ. Детектор регистрирует нейтроны, вылетающие под углом 900 к направлению пучка дейтонов. Определите кинетическую энергию нейтронов, если в реакции
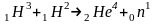 выделяется энергия 14МэВ
(10,4МэВ).
выделяется энергия 14МэВ
(10,4МэВ).В баллистический маятник массой М=2,1кг, подвешенный на растяжимых нитях длиной l=1,1м, попадает горизонтально летящая пуля массой m=9,0г. Определите начальную скорость пули, если маятник смещается от положения равновесия на расстояние S=23см (162м/с).
Две одинаковые лодки движутся параллельным курсом с одинаковыми скоростями. Как будут двигаться лодки после того, как обменяются равными грузами? Грузы перебрасываются одновременно и перпендикулярно направлению движения лодок с одинаковыми по величине скоростями.
Ствол пушки направлен под углом α=600 к горизонту. Когда колеса пушки закреплены, скорость снаряда равна u=500м/с. Определите скорость отката пушки после выстрела, если её колеса освободить. Масса пушки в 50 раз больше массы снаряда (-5,0м/с).
Баба копра массой m=600кг падает на сваю массой M=300кг с высоты h=0,5м. При этом свая проникает в грунт на глубину d=0,1м. Определите силу сопротивления грунта, считая удар бабы копра о сваю абсолютно неупругим (200кН).
Между шариками массой m1=50г и m2=150г находится сжатая легкая пружина. Если первый шарик удерживать на месте, а второй освободить, то он отлетает со скоростью u=2,4м/с. С какой скоростью будут двигаться шары, если оба шарика освободить одновременно? Начальные деформации пружины в обоих случаях одинаковы (-3,6м/с; 1,2м/с).
Нейтрон с кинетической энергией Eк=254кэВ налетает на неподвижное ядро
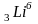 .
При этом образуется возбужденное ядро
.
При этом образуется возбужденное ядро
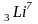 .
Определите кинетическую энергию ядра
(35кэВ).
.
Определите кинетическую энергию ядра
(35кэВ).Неподвижное тело в результате взрыва распадается на два осколка с массами m1=0,6кг, m2=2,4кг. Определите скорости осколков, если при взрыве выделяется энергия Е=120Дж (18м/с; 4,5м/с).
На тело массой 0,5кг, подвешенное на нерастяжимой нити, падает горизонтально движущееся тело массой m=100г и слипается с ним. При столкновении выделяется теплота Q=17Дж. На какую высоту поднимется система после столкновения? (57см).
При разрыве гранаты, летящей со скоростью u=10м/с, образовалось три равных осколка с массами по m=1кг. Общая кинетическая энергия всех осколков оказалась равной Eк=475Дж. Первый осколок летит в направлении полета гранаты, а два других летят перпендикулярно полёту гранаты. Определите начальные скорости осколков после взрыва гранаты (30м/с; 5м/с; 5м/с).
Может ли произойти ионизация атома цезия–133 ударом атома кислорода–16 с кинетической энергией Ек=4,0эВ? Энергия ионизации цезия–133 равна Е=3,9эВ (нет).
Альфа-частица, летящая со скоростью u=1,0км/с, испытывает упругое столкновение с неподвижным ядром и летит под углом 900 к первоначальному направлению движения. Масса ядра mя=5mα. Определите скорости uα и uя после столкновения (870м/с; 260м/с).
Примеры решения задач (Движение по окружности)
Задача 33. Шарик массой m=27г, подвешенный на нерастяжимой нити, отклонили от положения равновесия в горизонтальное положение и отпустили. В каком положении нить оборвется, если прочность нити на разрыв равна Fпр=0,18Н. Сопротивлением воздуха пренебречь
Р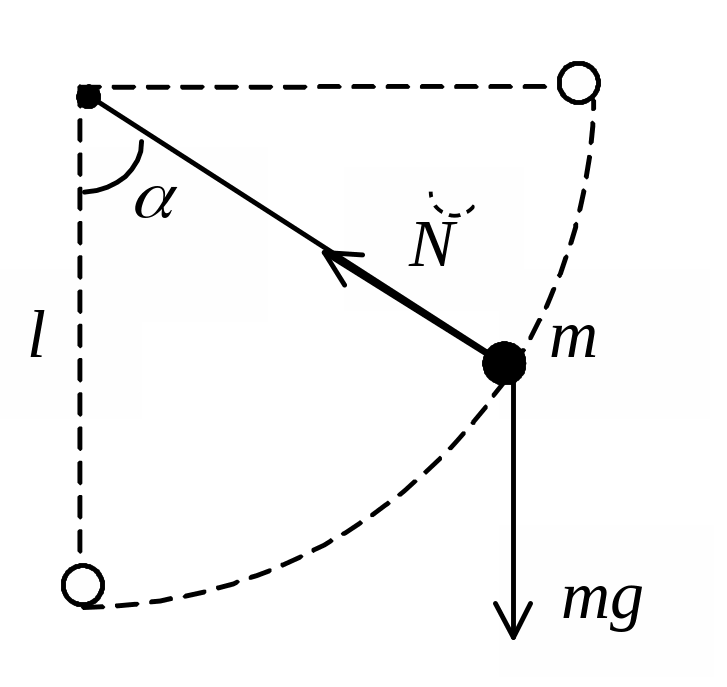 ешение.
Рассмотрим
динамическое решение задачи. Шарик
движется по окружности, радиус которой
равен длине нити l,
под действием силы тяжести
ешение.
Рассмотрим
динамическое решение задачи. Шарик
движется по окружности, радиус которой
равен длине нити l,
под действием силы тяжести
и силы реакции нити .
Основной закон динамики
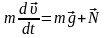
представим в проекциях на направление скорости в каждой точке окружности и направление вдоль нити:
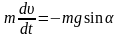 , (1)
, (1)
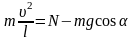 . (2)
. (2)
Из уравнения (2) видно, что при падении шарика сила реакции нити возрастает, и нить может оборваться, когда реакция нити сравняется с прочностью нити (N=Fпр).
Точка отрыва характеризуется углом aобр, который связан со скоростью шарика в точке обрыва соотношением
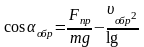 . (3)
. (3)
Скорость шарика в момент обрыва можно найти, используя закон сохранения механической энергии (убедитесь в этом самостоятельно) или решая уравнение (1):
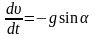 .
.
Чтобы проинтегрировать это уравнение, воспользуемся следующим преобразованием. Умножим левую и правую часть уравнения на элементарное смещение по дуге окружности dS, которое геометрически связано с угловым смещением da соотношением
dS=lda .
Учитывая,
что
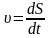 ,
после интегрирования получим
,
после интегрирования получим
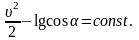
Постоянная определяется начальным состоянием (a=900,u=0).
Скорость шарика является однозначной функцией угла a:
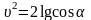 . (4)
. (4)
Окончательно, из соотношений (3) и (4), находим
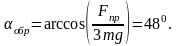
Задача 34. Тело массой m=0,5кг, подвешенное на упругой нити жесткостью k=150Н/м, отвели от положения равновесия, не деформируя нити, на угол a=600 и отпустили. Определите силу натяжения нити при прохождении телом положения равновесия, если длина недеформированной нити равна l0=1,0 м.
Р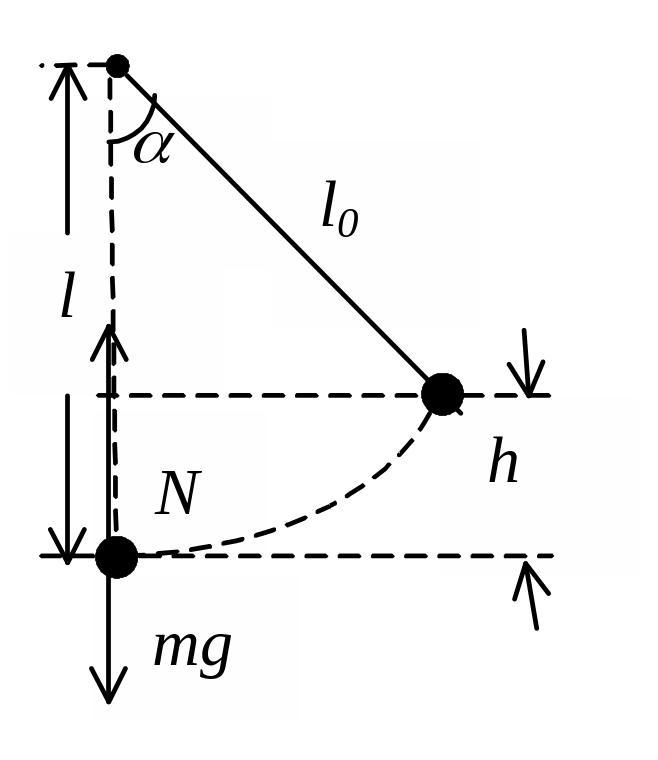 ешение.
Сила
натяжения нити при прохождении положения
равновесия равна
ешение.
Сила
натяжения нити при прохождении положения
равновесия равна
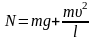 , (1)
, (1)
где N=k(l-l0)=kDl.
Скорость тела в положении равновесия найдем из закона сохранения механической энергии
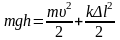 , (2)
, (2)
где h=l - l0 cosa.
Из (1)
и (2)
получаем
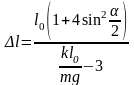 .
.
Натяжение нити при прохождении положения равновесия равно
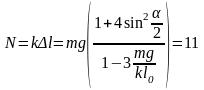 Н.
Н.
В
предельном случае нерастяжимой нити
(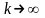 )
и угле a=900
получается известный результат (убедитесь
в этом):
)
и угле a=900
получается известный результат (убедитесь
в этом):
N=3mg .
Задача
35. По вогнутой
сферической поверхности радиусом R
скользит
небольшое тело из положения с полярным
углом
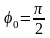 без начальной скорости. Найдите
зависимость скорости тела от полярного
угла u(j),
если коэффициент трения скольжения
между телом и поверхностью равен m
=1,0.
Сопротивлением воздуха пренебречь.
без начальной скорости. Найдите
зависимость скорости тела от полярного
угла u(j),
если коэффициент трения скольжения
между телом и поверхностью равен m
=1,0.
Сопротивлением воздуха пренебречь.
Р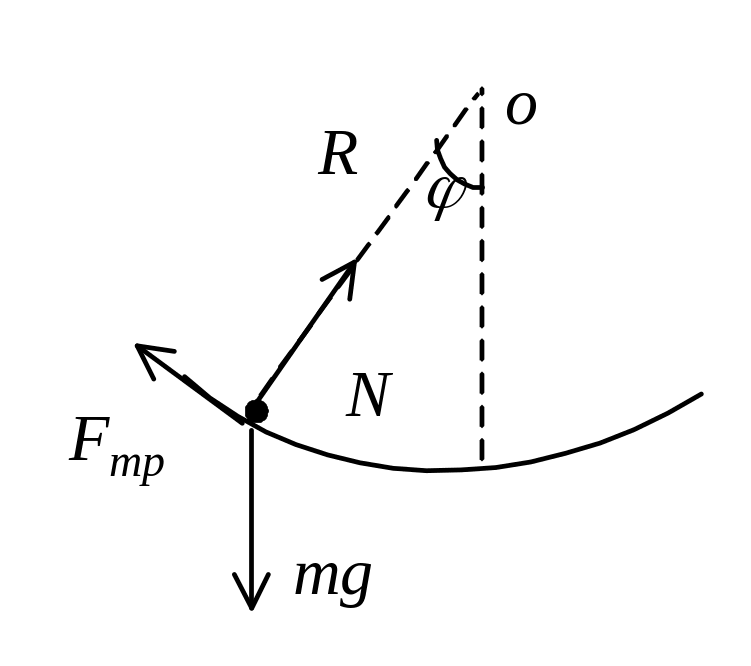 ешение.
Проведем
предварительный анализ. Под действием
указанных на рисунке сил тело начнет
двигаться к положению равновесия, если
tgj>m,
и остановится в положении, для которого
будет выполнено условие tgj£m.
ешение.
Проведем
предварительный анализ. Под действием
указанных на рисунке сил тело начнет
двигаться к положению равновесия, если
tgj>m,
и остановится в положении, для которого
будет выполнено условие tgj£m.
Представим основное уравнение динамики в проекциях на направление скорости и радиальное направление:
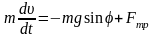 , (1)
, (1)
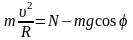 , (2)
, (2)
где Fтр=mN.
После некоторых преобразований (проделайте их самостоятельно), учитывая, чтo dS=Rdj, получим уравнение для квадрата скорости тела в зависимости от его положения на сфере, определяемое полярным углом j.
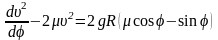 . (3)
. (3)
Решение этого дифференциального уравнения должно удовлетворять условию u2(j0)=0.
Представим
уравнение (3)
в обобщенной форме в безразмерных
переменных. Для этого скорость тела
измерим в долях
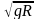 :
:
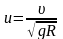 .
.
Решение обобщенного уравнения
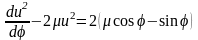
при начальном условии u2(j0)=0 имеет вид
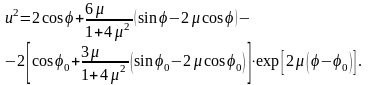
Убедитесь в правильности решения и исследуйте его на предельные переходы (m=0, m<<1, j0<<1).
Для численных данных в условии задачи
u2(j)=0,4[3sina - cosj - 3exp(2j - p)].
Убедитесь,
что тело остановится, не доходя до
положения равновесия, на угловом
расстоянии 0,417
рад (23,90),
а максимальную скорость, равную 2,2м/с,
тело будет иметь при полярном угле 1,087
(62,3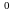 ).
).
Задача 36. На твердый стержень, расположенный под углом a=450 к вертикали, насажена бусинка. Стержень вращается с угловой скоростью w=30 рад/с вокруг вертикальной оси. Коэффициент трения между стержнем и бусинкой равен m=0,8. Описать движение бусинки по стержню.
Решение. Бусинка движется под действием силы тяжести , силы реакции и силы трения .
Положение бусинки на стержне будет неоднозначным, так как величина и направление силы трения покоя может меняться от нуля до максимального значения, равного mN.
Крайние положения равновесия бусинки на стержне А и В определяются максимальными значениями сил трения покоя, которые препятствуют смещению бусинки вниз в точке А и вверх в точке В.
Р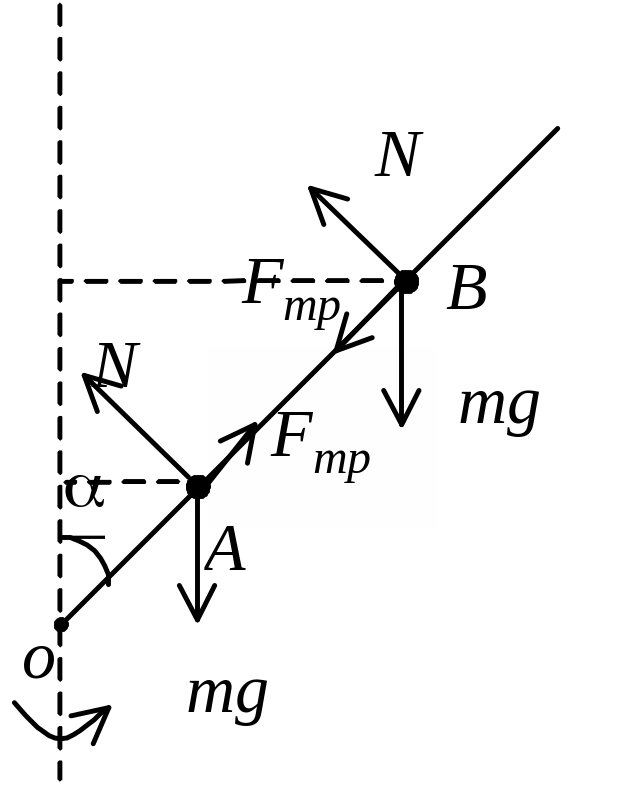 ассмотрим
положения равновесия
бусинки
в точке А.
Бусинка
неподвижна относительно стержня в точке
А,
если выполнены
условия
ассмотрим
положения равновесия
бусинки
в точке А.
Бусинка
неподвижна относительно стержня в точке
А,
если выполнены
условия
Ncosa - Fтрsina=mw2rA,
Nsina + Fтрcosa=mg,
где Fтр=mN, rA=lAsina (lA – расстояние от точки О до точки А вдоль стержня).
Откуда для lA находим
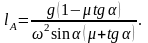
Бусинка удерживается на стержне в точке А силой трения покоя, если угол a удовлетворяет условию
a<arctg(1/m).
Аналогично, рассматривая условие равновесия бусинки на стержне в точке В, находим
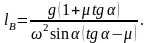
Бусинка удерживается на стержне в точке В, если угол a удовлетворяет условию
a>arctg(1/m).
Таким образом, бусинка может находиться в равновесии на стержне в любой точке интервала lA£l£lB при условии
arctgm<a<arctg(1/m).
Для численных данных в условии задачи 390<a<510.
Угол наклона стержня a=450 удовлетворяет условию существования равновесия на стержне в положениях, определяющихся неравенством 2,5см<l<20см.
В случае идеально гладкого стержня (m=0) равновесное положение бусинки
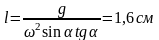
будет неустойчивым.
Бусинка будет скользить вверх или вниз по стержню в результате случайного отклонения, удаляясь от положения неустойчивого равновесия. Устойчивому положению равновесия соответствует l=0.
З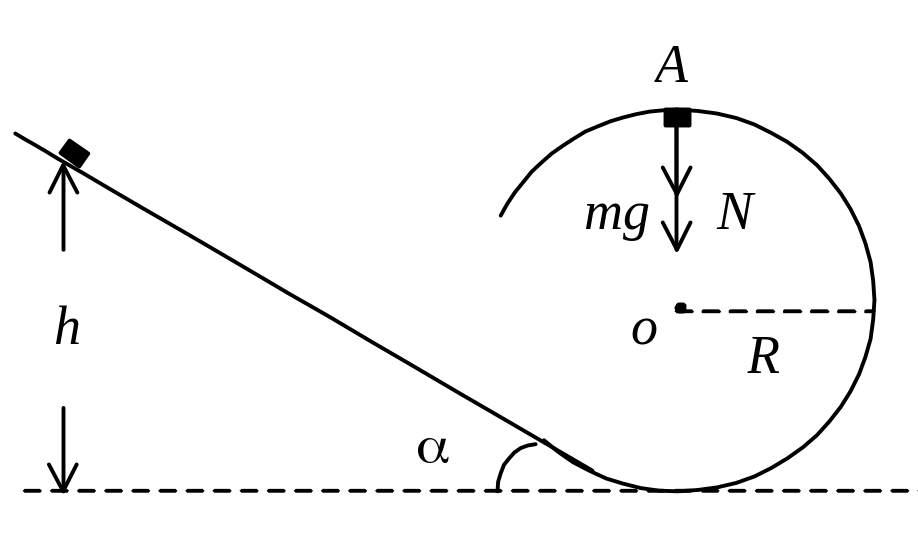 адача
37. Горка в
форме наклонной поверхности плавно
переходит в цилиндрическую поверхность
радиусом R=0,53м.
С какой
максимальной высоты hm(м)
необходимо спустить небольшое тело,
чтобы оно смогло преодолеть “мертвую
петлю”? Угол наклона горки к горизонту
равен
a=320,
коэффициент трения между телом и горкой
m=0,15.
Небольшой участок плавного перехода и
внутреннюю поверхность цилиндра можно
считать гладкими
(m=0).
Тело начинает двигаться из состояния
покоя.
адача
37. Горка в
форме наклонной поверхности плавно
переходит в цилиндрическую поверхность
радиусом R=0,53м.
С какой
максимальной высоты hm(м)
необходимо спустить небольшое тело,
чтобы оно смогло преодолеть “мертвую
петлю”? Угол наклона горки к горизонту
равен
a=320,
коэффициент трения между телом и горкой
m=0,15.
Небольшой участок плавного перехода и
внутреннюю поверхность цилиндра можно
считать гладкими
(m=0).
Тело начинает двигаться из состояния
покоя.
Решение. Вначале выясним, выполняется ли условие скольжения тела по наклонной плоскости горки. Чтобы тело скользило вниз, то должно выполняться условие a>arctgm. В нашем случае это условие выполнимо (убедитесь в этом).
Высоту спуска h необходимо подобрать так, чтобы тело смогло подняться до точки А и не оторвалось от нее.
Рассмотрим условие прохождения точки А. Воспользуемся для анализа основным законом динамики
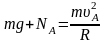 .
.
Сила реакции NA определяется скоростью тела в точке А. Минимальную скорость тела в точке А uAmin, при которой тело проходит критическую точку, найдем с учетом условия NA=0 :
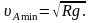
Следовательно, в критической точке механическая энергия тела не может быть меньше
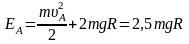 .
.
Очевидно, величина запаса энергии должна быть такой, чтобы обеспечить надлежащий уровень механической энергии в критической точке и компенсировать потерю механической энергии, связанную с работой силы трения при движении тела по горке:
E=EA+A,
где E=mghm (начальная скорость равна нулю), A=mmghmctga.
Из последнего соотношения получаем
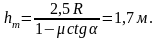
Если трением на цилиндрической поверхности пренебречь нельзя, то при равенстве коэффициентов трения на горке и цилиндрической поверхности для минимальной высоты получается
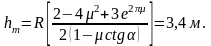
Из полученных соотношений в пределе для идеально гладких поверхностей получается известный результат:
hm=2,5R=1,3 м.
Точность оценки существенно зависит от принятой модели.
Задача 38. На вершине сферы радиусом R=0,26м находится небольшое тело, которому сообщили начальную скорость u0=1,2м/с в горизонтальном направлении. Коэффициент трения между телом и поверхностью сферы равен m=0,1. В какой точке тело отрывается от сферы? Чему равна скорость тела в момент отрыва от поверхности сферы? Сопротивлением воздуха пренебречь.
Решение.
В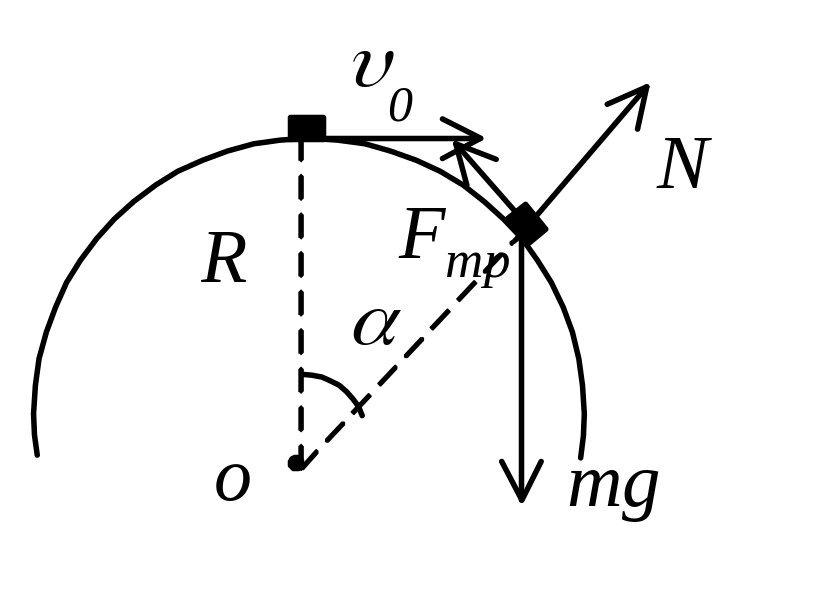 такой постановке задача более близка
к реальной действительности, но становится
сложной в математическом отношении.
Очевидно, при больших значениях
коэффициента трения влияние силы трения
на характер движения будет существенным,
но при малых
такой постановке задача более близка
к реальной действительности, но становится
сложной в математическом отношении.
Очевидно, при больших значениях
коэффициента трения влияние силы трения
на характер движения будет существенным,
но при малых
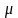 (каких?)
предположение о гладкости сферы может
оказаться вполне приемлемым. Количественную
оценку последнему можно дать, только
решив предложенную задачу или проведя
эксперимент.
(каких?)
предположение о гладкости сферы может
оказаться вполне приемлемым. Количественную
оценку последнему можно дать, только
решив предложенную задачу или проведя
эксперимент.
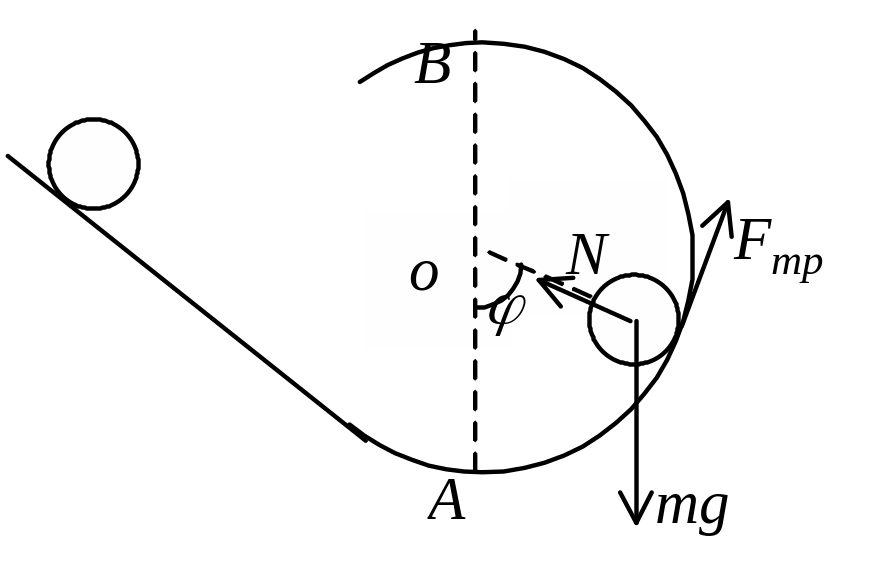
Проведем теоретическое исследование поставленной задачи. Тело на сфере находится под действием силы тяжести , силы реакции и силы трения (см. рисунок).
Для анализа воспользуемся основным уравнением динамики в скалярной форме:
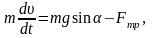
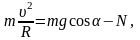
где Fтр=mN.
Из этой системы уравнений после несложных преобразований (см. задачу 33) получим следующее уравнение относительно квадрата скорости тела:
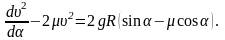
Представим последнее уравнение в обобщенной форме в безразмерных величинах:
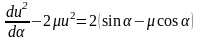 ,
,
где - безразмерная скорость.
Его
частное решение должно удовлетворять
условию
a=0,
u=u0,
где
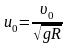 .
.
Полученное уравнение является линейным дифференциальным уравнением второго порядка, частное решение которого имеет вид
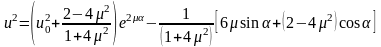 .
.
Убедитесь самостоятельно в том, что полученное решение в пределе переходит в решение для идеально гладкой сферы.
Для силы реакции сферы получаем
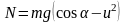 .
.
Откуда,
положив
N=0,
находим уравнение для полярного угла,
соответствующего точке отрыва,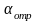 :
:
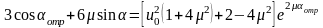 .
.
Для m=0
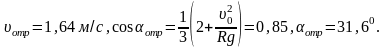
Для m=0,1
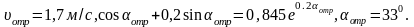
Для m=0,5
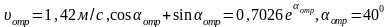 .
.
Из расчетов видно, что при значениях коэффициента трения m£0,1 расхождение в результатах в сравнении со случаем гладкой сферы (m=0) незначительно (не более 6 %).
Задача 39. Профиль края горизонтального стола скруглен в полуокружность радиусом R=0,55м. Небольшому телу сообщили горизонтальную скорость u0=3,5м/с. Определите точку отрыва тела на скруглении, если в начальный момент времени тело находилось на расстоянии S=4,2м от начала скругления. Коэффициент трения между телом и горизонтальной поверхностью принять равным m=0,11, а скругление считать гладким.
Решение .Сначала оценим, достигнет ли тело точки А (начало скругления). Начальная кинетическая энергия тела должна быть не меньше работы силы трения на горизонтальном участке пути S.
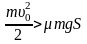 .
.
Отсюда находим условие для оценки начальной скорости тела:
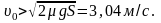
В нашем случае условие выполнено.
В точке А тело будет иметь скорость
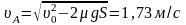 .
.
Начиная с точки А, тело движется по окружности без трения, если не отрывается в точке А. Запишем основное уравнение динамики для точки А:
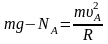 .
.
Из уравнения следует, что тело отрывается в точке А (NA=0), если его скорость в этой точке будет равна
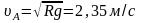 .
.
В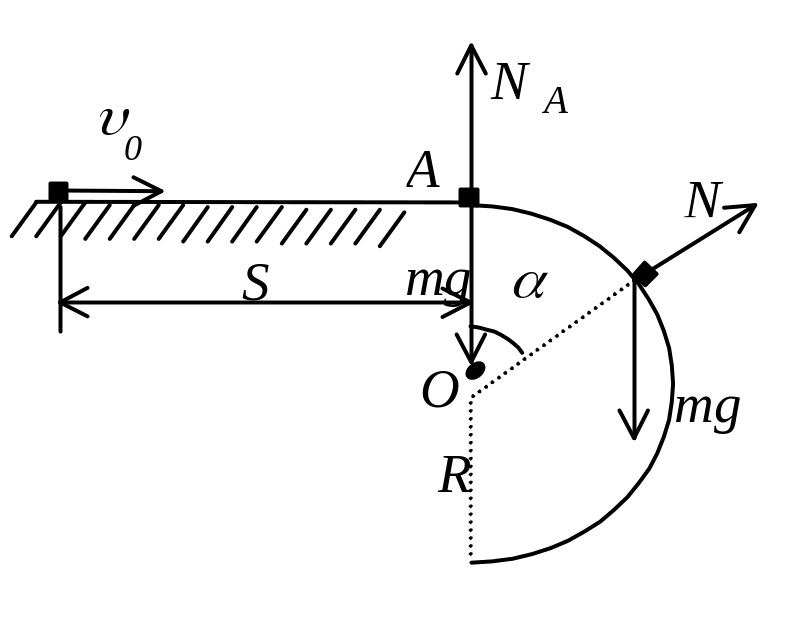 нашем случае точка отрыва лежит ниже
точки А.
нашем случае точка отрыва лежит ниже
точки А.
Исследуем движение тела по гладкому скруглению. В произвольной точке на скруглении тело находится под действием силы тяжести и силы реакции (см. рисунок ):
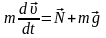 .
.
Представим основное уравнение динамики в скалярной форме:
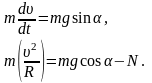
В точке отрыва N=0. Из второго уравнения получаем соотношение, связывающее скорость в точке отрыва uотр и полярный угол, соответствующий точке отрыва, aотр:
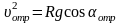 .
.
Решая первое уравнение (см. задачу 33) при условии, что u(0)=uA, находим
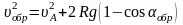 .
.
Окончательно для определения полярного угла точки отрыва получим
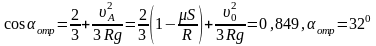 .
.
Скорость тела в точке отрыва равна
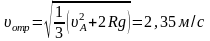 .
.
В случае гладкой сферы (m=0) при uА=0 получается известный результат:
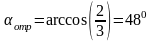 .
.
Учет силы трения на скруглении усложняет решение. В конечном счет проблема сводится к определению корня трансцендентного уравнения (см. задачу 37).
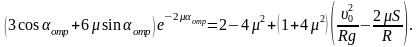
Для данных в условии задачи aотр=300.
Задачи для самостоятельного решения (Движение по окружности)
1. На какой максимальный угол можно отклонить шарик, чтобы нить подвеса не оборвалась при прохождении положения равновесия. Нить выдерживает нагрузку в 2mg, где m-масса шарика (600).
2. На нити длиной l=98см подвешен шар массой m1=1,0кг, радиусом R=4,0 см. В шар попадает горизонтально летящая пуля и застревает в нем. Масса пули m2=10, скорость пули u0=400м/с. Оборвется ли нить, если она выдерживает нагрузку в 30Н? (нет).
3. Небольшой груз, подвешенный на нерастяжимой нити длиной l=1,0м, отклонили от положения равновесия на угол 900 и отпустили, сообщив скорость в направлении равновесия, равную 3,0м/с. В каком положении груза нить оборвется, если она выдерживает нагрузку, равную 3mg (m-масса груза) ? (460).
4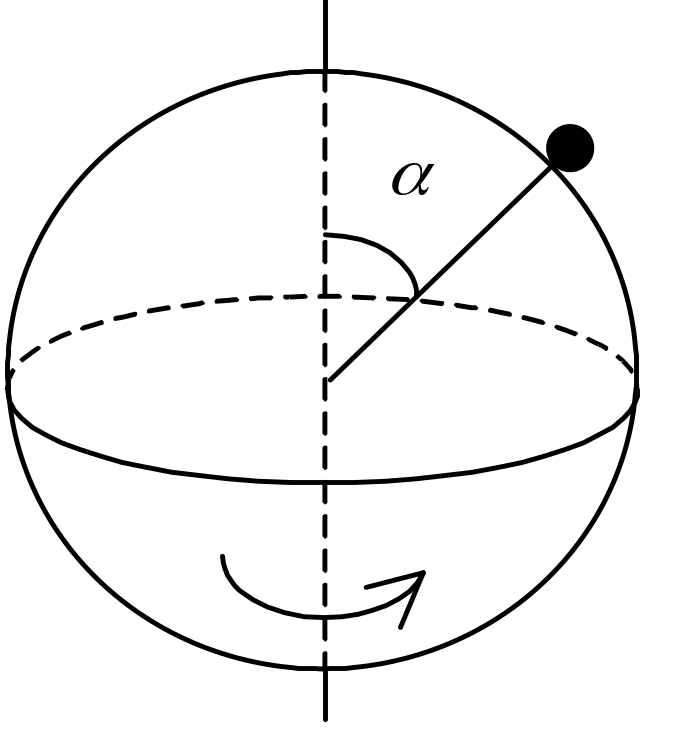 .
На сферической поверхности радиусом
R=0,5м
находится небольшое тело. Коэффициент
трения между телом и поверхностью сферы
m=0,8.
Угол a=300
(см. рисунок). Определите предельную
угловую скорость вращения сферы, при
которой тело удерживается на поверхности
сферы (2,5
рад/с).
.
На сферической поверхности радиусом
R=0,5м
находится небольшое тело. Коэффициент
трения между телом и поверхностью сферы
m=0,8.
Угол a=300
(см. рисунок). Определите предельную
угловую скорость вращения сферы, при
которой тело удерживается на поверхности
сферы (2,5
рад/с).
5. На внутренней поверхности сферы радиусом R=0,15 м, которая вращается вокруг вертикальной оси, проходящей через центр сферы, находится небольшое тело. С какой предельной угловой скоростью может вращаться сфера, чтобы тело находилось в точке, направление на которую из центра сферы составляет с вертикалью угол в 450? Коэффициент трения между телом и поверхностью сферы равен 0,67 (22рад/с).
6. Метатель посылает молот массой m=6,0кг на расстояние S=60м по траектории, которая обеспечивает наибольшую дальность броска. Оцените максимальную силу, которая действует на метателя при ускорении молота, если разгон ведется по окружности радиусом R=2,0м. Сопротивление воздуха при оценке не учитывать (1,8 кН).
7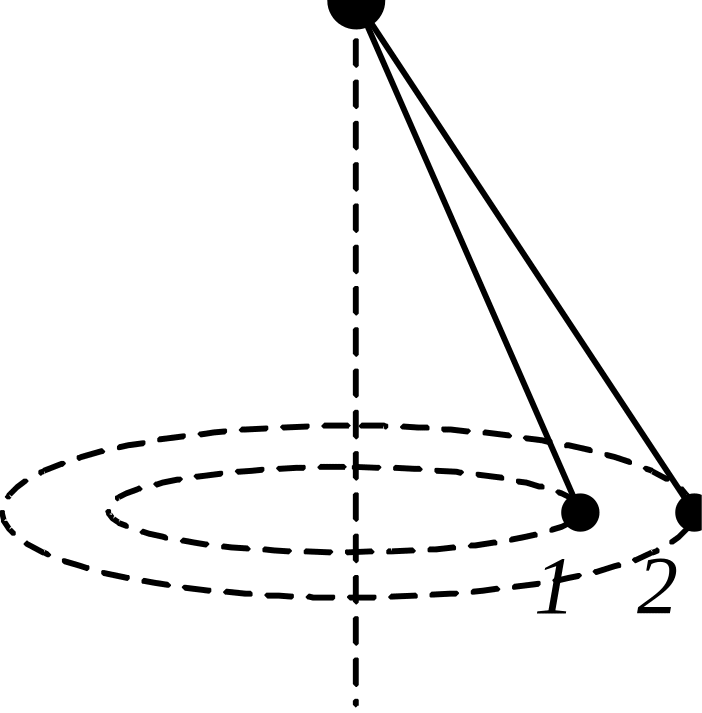 .
Два шарика подвешены на нерастяжимых
нитях (см. рисунок), вращаются в одной
горизонтальной плоскости по окружностям
радиусами R1
и R2.
Сравните периоды вращения шариков
(T1=T2).
.
Два шарика подвешены на нерастяжимых
нитях (см. рисунок), вращаются в одной
горизонтальной плоскости по окружностям
радиусами R1
и R2.
Сравните периоды вращения шариков
(T1=T2).
8. Коэффициент трения покоя между шинами автомобиля и полотном дороги летом больше в N раз, чем зимой. Предельные скорости автомобиля на повороте летом и зимой относятся как Nк.Определите степень к (0,5).
9. Небольшой шарик массой m=55г прикреплен к концу упругой нити, жесткость которой к=43Н/м. Нить с шариком отвели в горизонтальное положение и отпустили. Когда груз проходил положение равновесия, длина нити оказалась равной l=1,1м. Определите силу натяжения нити при прохождении грузом положения равновесия (1,6Н).
10. Небольшое тело начинает скользить с высоты h=1,2м без начальной скорости по наклонному желобу, переходящему в полуокружность радиусом R=55см. Пренебрегая трением, оцените скорость тела в точке отрыва (2,1м/с).
11. Автомобиль движется по выпуклому мосту, имеющему профиль дуги окружности радиусом R=30м. Определите скорость движения автомобиля, если в верхней точке моста сила давления на мост равна ¼mg (m-масса автомобиля) (15м/с ).
12. На экваторе некой планеты тела весят в 2 раза меньше, чем на полюсе. Средняя плотность вещества этой планеты равна 3,0г/см3. Чему равны сутки на этой планете ? (2,7 часа).
1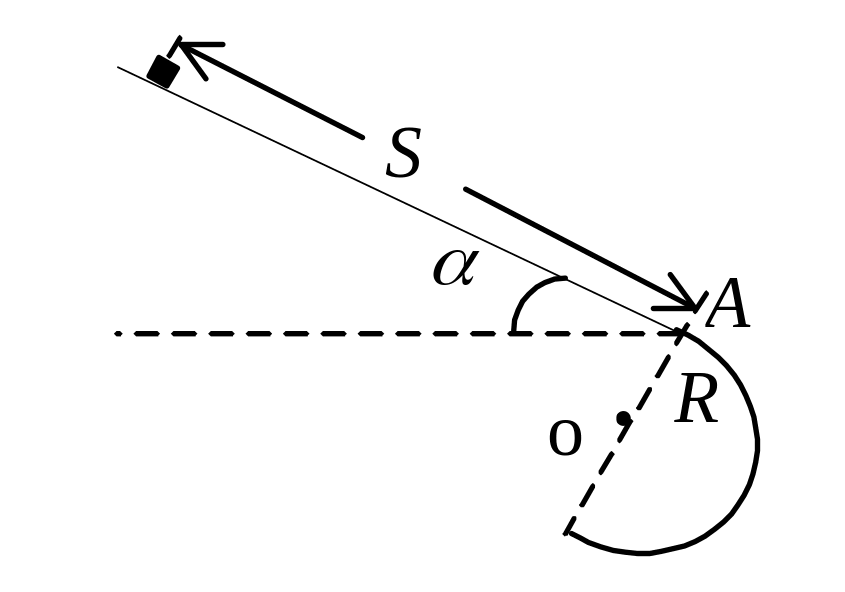 3.
На каком минимальном расстоянии S(м)
от точки А
(см.рисунок)
необходимо поместить тело, чтобы оно
оторвалось от поверхности в этой точке?
Угол наклона плоскости, по которой
движется тело, равен a=450.
Радиус
скругления R=0,8 м.
Коэффициент трения между телом и
плоскостью
3.
На каком минимальном расстоянии S(м)
от точки А
(см.рисунок)
необходимо поместить тело, чтобы оно
оторвалось от поверхности в этой точке?
Угол наклона плоскости, по которой
движется тело, равен a=450.
Радиус
скругления R=0,8 м.
Коэффициент трения между телом и
плоскостью
=0,2 (0,35м).
14.
Оцените массу нашей Галактики, принимая
во внимание, что Солнце находится на
краю Галактики на расстоянии ~104
парсек от
её центра и имеет орбитальную скорость
~300км/с.
1парсек@3,08×1016м
(~ 4×10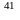 кг).
кг).
15. Мотоциклист едет по внутренней поверхности вертикального цилиндра радиусом R=5,8м. Центр тяжести человека и мотоцикла расположен на расстоянии l=0,8м от стенки цилиндра. Коэффициент трения между колесами и стенкой m=0,5. С какой максимальной скоростью может ехать мотоциклист по горизонтальной окружности цилиндра ? (10м/с).
16. На твердый стержень, расположенный под углом =320 к вертикали, насажен небольшой шарик. Стержень вращается с частотой n=2,1об/с вокруг вертикальной оси. Коэффициент трения между стержнем и шариком равен m=0,34. Оцените интервал расстояний до оси вращения равновесного положения шарика на стержне (4,7см;24см).
17. Наклонная плоскость плавно переходит в цилиндрическую поверхность радиусом R=0,64м. Небольшое тело скользит по наклонной плоскости с высоты h=3,4м без начальной скорости. Угол наклона плоскости к горизонту равен =450 . Коэффициент трения между телом и плоскостью m=0,57. Небольшой участок плавного перехода и внутреннюю поверхность цилиндра можно считать гладкими (m=0). Определите высоту точки отрыва тела от поверхности цилиндра (1,1м).
18. На вершине сферы радиусом R=0,37м находится небольшое тело, которому сообщили начальную скорость u0=1,4м/с в горизонтальном направлении. Коэффициент трения между телом и поверхностью сферы равен m=0,35. Определите скорость тела в момент отрыва его от поверхности сферы (2,17м/с).
19.
Космическая станция массой 100т
вращается на круговой орбите на высоте
600км
над поверхностью Земли. Сила трения,
действующая на станцию в верхних слоях
атмосферы, равна F=-cun,
где u
-орбитальная
скорость станции. Станция за сутки
снижается на Dh=4,3м.
Определите значения с
и n.
Радиус Земли принять равным 6400км
(с=6×10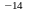 кгс/м2,
n=3).
кгс/м2,
n=3).
20. В результате трения в верхних слоях атмосферы механическая энергия спутника Земли уменьшилась на 4%. Орбита спутника при этом осталась круговой. Определите период обращения спутника, если вначале спутник вращался на высоте 500км над поверхностью Земли. Радиус Земли принять равным 6400км (90мин).
Примеры решения задач (Поступательное и вращательное движение твердого тела)
Задача 40. Маятник Обербека представляет собой твердое симметрическое тело, вращающееся вокруг собственной оси. Вдоль радиальных спиц маятника можно передвигать одинаковые грузы массой m0=255г и закреплять их на равном расстоянии R от оси маятника. К шкиву маятника радиусом r=5,9см привязана нить длиной l=1,1м, к концу которой подвешен груз массой m=210г. Момент инерции маятника без грузов m0 равен J0=0,013кгм2. Определите момент силы трения в оси маятника, если груз m падает с высоты h=l за время t=3,1с. Число спиц n=4. Грузы m0 закреплены на расстоянии R=12см.
Р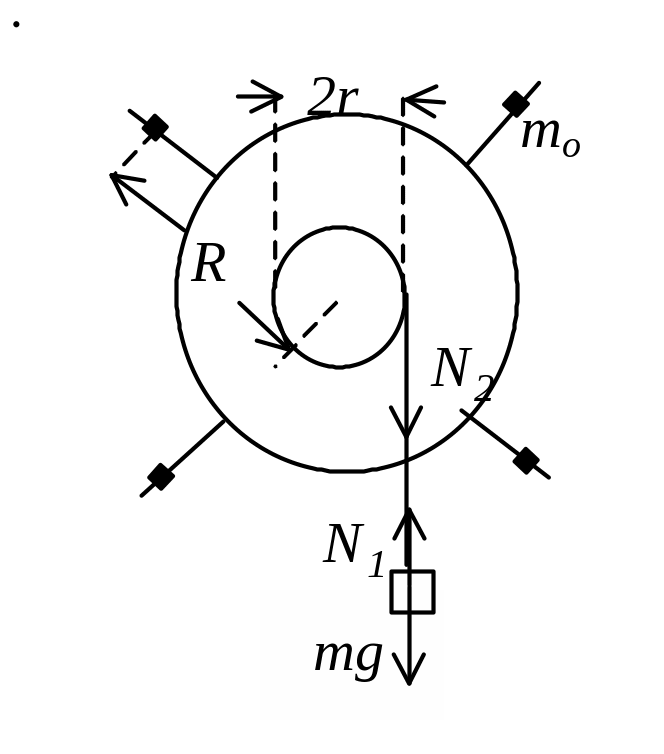 ешение.
Маятник вращается под действием момента
силы натяжения нити N2×r
и момента силы трения в оси вращения
Мтр,
а груз m
движется поступательно под действием
силы тяжести
ешение.
Маятник вращается под действием момента
силы натяжения нити N2×r
и момента силы трения в оси вращения
Мтр,
а груз m
движется поступательно под действием
силы тяжести
и
силы натяжения нити
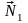 .
Уравнения
движения маховика и груза имеют вид:
.
Уравнения
движения маховика и груза имеют вид:
N2r-Мтр=Je , (1)
mg-N1=ma , (2)
где a=er , N1=N2, если нить нерастяжима, J=J0+nm0R2 – момент инерции маятника относительно оси вращения согласно теореме Штейнера.
Ускорение падения груза m равно
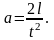
Из системы уравнений (1) и (2) получаем
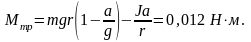
З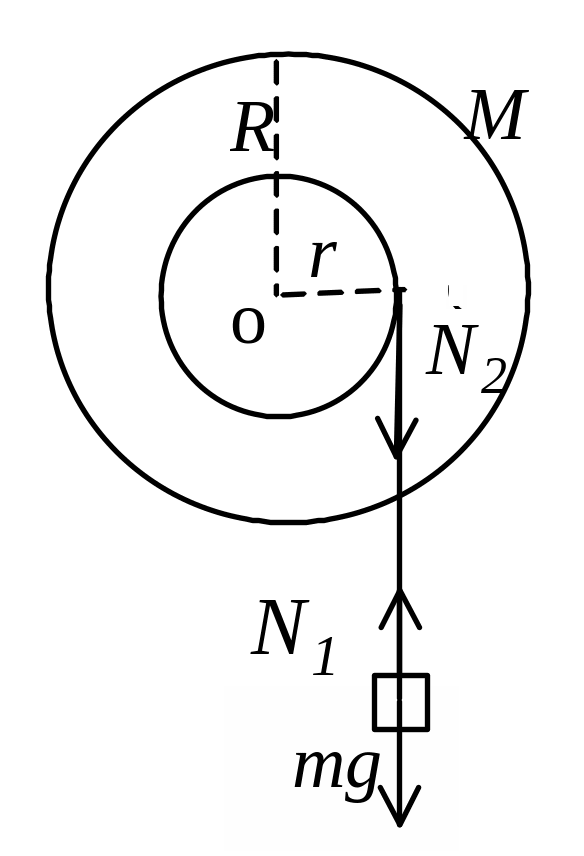 адача
41. Маховик
в форме сплошного однородного диска
радиусом R=13см
и массой М=1,2
кг насажен
на горизонтальную ось, проходящую через
его центр. К маховику приварен соосный
тонкостенный цилиндр радиусом r.
Массой цилиндра можно пренебречь. На
цилиндр намотан шнур, к свободному концу
которого привязан груз массой m=2,5кг.
Определите,
при каком значении радиуса цилиндра rm
угловое ускорение маховика будет
наибольшим. С каким ускорением движется
при этом груз m?
Трением в оси вращения, сопротивлением
воздуха и массой шнура пренебречь.
адача
41. Маховик
в форме сплошного однородного диска
радиусом R=13см
и массой М=1,2
кг насажен
на горизонтальную ось, проходящую через
его центр. К маховику приварен соосный
тонкостенный цилиндр радиусом r.
Массой цилиндра можно пренебречь. На
цилиндр намотан шнур, к свободному концу
которого привязан груз массой m=2,5кг.
Определите,
при каком значении радиуса цилиндра rm
угловое ускорение маховика будет
наибольшим. С каким ускорением движется
при этом груз m?
Трением в оси вращения, сопротивлением
воздуха и массой шнура пренебречь.
Решение. В данной связанной системе тел груз m движется поступательно под действием силы тяжести и силы натяжения шнура , а маховик вращается вокруг неподвижной оси под действием момента силы натяжения шнура N2r. Уравнения движения маховика и груза имеют вид:
N2r=J0e , (1)
mg-N1=ma, (2)
где J0=1/2MR2 – момент инерции маховика относительно ос вращения.
Из условия невесомости шнура следует, что
N1=N2. (3)
Кроме того, если можно пренебречь растяжимостью шнура, то ускорение груза m и касательное ускорение точек обода цилиндра будут равны:
a=at=er. (4)
Из уравнений (1) и (2) с учетом условий (3) и (4) получаем для углового ускорения вращения маховика
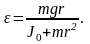
Как видно, угловое ускорение является функцией радиуса r. Эта зависимость e(r) имеет максимум ( убедитесь в этом ) при
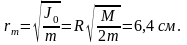
Груз при этом будет падать с ускорением
a=g/2=5,0м/с2.
Задача 42. На подвижной призме с углами при основании a=300 и b=450 находится система двух связанных тел массами m1=1,1кг и m2=4,2кг. Тела связаны нерастяжимой нитью, перекинутой через блок массой mб=0,46кг, закрепленной в вершине призмы. Коэффициент трения между телами и гранями призмы равен m=0,5. Как будет двигаться система грузов, если нить не проскальзывает по блоку, а трением в оси блока можно пренебречь.
Решение .Выясним, в какую сторону будет двигаться система грузов – по часовой стрелке или против. Рассмотрим условия вращения системы по часовой стрелке. Первое тело должно подниматься вверх по грани с углом наклона a, а второе – опускаться вниз по грани с углом наклона b. Поэтому должны выполняться условия:
F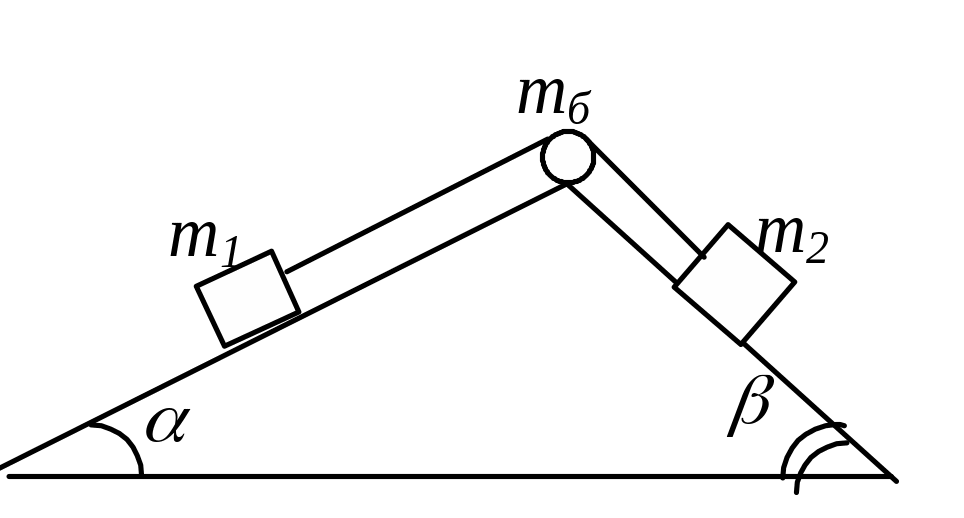 1-
m1gsina-m
m1gcosa³0,
1-
m1gsina-m
m1gcosa³0,
m2gsinb-m m2gcosb-F2³0,
F1>F2,
где F1,F2 – силы натяжения нити слева и справа от блока.
Из этих условий получаем соотношение между массами тел, при котором система движется по часовой стрелке:
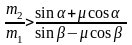 ,
,
если m<tgb.
Аналогично, рассматривая возможное движение системы против часовой стрелки, находим
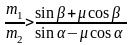 ,если
m<tga.
,если
m<tga.
Таким образом, для всех значений m2/m1 , удовлетворяющих неравенству
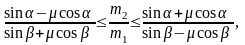
система тел покоится на призме.
Для численных данных в условии задачи система движется по часовой стрелке (убедитесь в этом).
Поступательное движение тел по граням призмы и вращение блока описываются системой уравнений динамики:
m2g(sinb-mcosb)-F2=m2a2,
F1-m1g(sina+mcosa)=m1a1,
(F2- F1)R=Jбe ,
где Jб=1/2mбR2 (считая блок однородным диском).
Дополнительные соотношения, связывающие неизвестные величины a1, a2, e, определяются условием нерастяжимости нити и отсутствием проскальзывания нити по блоку :
a1=a2 =at=eR,
где R – радиус блока.
Из системы уравнений динамики находим
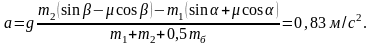
Из найденного решения можно получить множество частных решений. Например, при a=b=900 , mб=0 получается известное решение
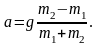
Решение для движения системы против часовой стрелки можно получить перестановкой масс и углов в найденном решении.
Задача 43. Круглое тело раскрутили до угловой скорости w0(рад/с) и поставили на горизонтальную поверхность. Коэффициент трения между телом и поверхностью равен m.. Оцените время торможения тела t(с), установившуюся скорость качения тела u(м/с), выделяющееся количество теплоты Q(Дж) и длину участка стабилизации качения S(м), если сопротивлением воздуха и трением качения можно пренебречь. Массу m(кг) и радиус R(м) тела считать заданными.
Р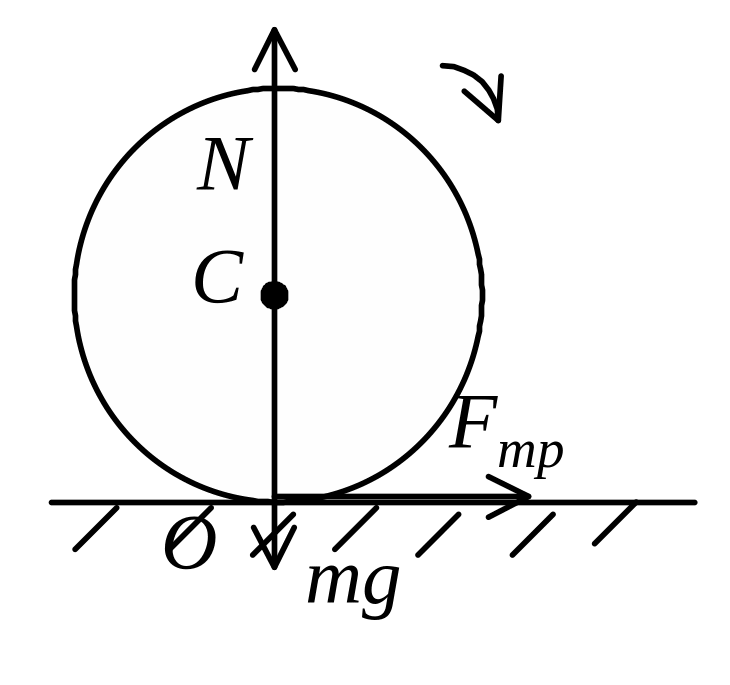 ешение
. Проанализируем
физическую ситуацию. Раскрученное тело
обладает кинетической энергией
ешение
. Проанализируем
физическую ситуацию. Раскрученное тело
обладает кинетической энергией
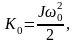
где J=CmR2 ,С – формпараметр круглого тела.
На горизонтальной поверхности тело находится под действием трех сил – силы тяжести , силы реакции и силы трения скольжения . Сила тяжести уравновешена силой реакции, поэтому процесс движения тела будет определяться только силой трения скольжения. В данном случае сила трения выполняет двоякую роль: с одной стороны, она тормозит вращательное движение, с другой – сообщает телу поступательное движение в горизонтальном направлении.
Энергетически это означает, что за счет убыли кинетической энергии вращения растет кинетическая энергия поступательного движения тела и наблюдается диссипация механической энергии.
Движение тела описывается уравнениями динамики
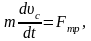 (1)
(1)
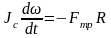 (2)
(2)
с начальными условиями w(0)=w0, uс(0)=0, где Fтр=mmg – сила трения скольжения, Jc=CmR2 – момент инерции круглого тела относительно оси, проходящей через центр инерции, uс - скорость движения центра инерции тела.
Из уравнений (1) и (2) получаем
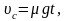

Скорость скольжения точки соприкосновения тела с поверхностью равна, очевидно, разности линейной скорости точек поверхности круглого тела и скорости поступательного движения тела:
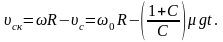
К моменту времени
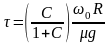
скорость скольжения становится равной нулю и наступает режим чистого качения.
В режиме чистого качения выполняется равенство
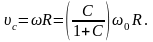
Длина участка стабилизации качения равна
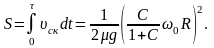
Количество выделяющейся теплоты можно определить, используя закон сохранения энергии или вычислив работу момента силы трения:
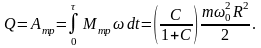
Отметим, что скорость установившегося поступательного движения uс и выделившееся количество теплоты Q не зависят от величины коэффициента трения скольжения m .
З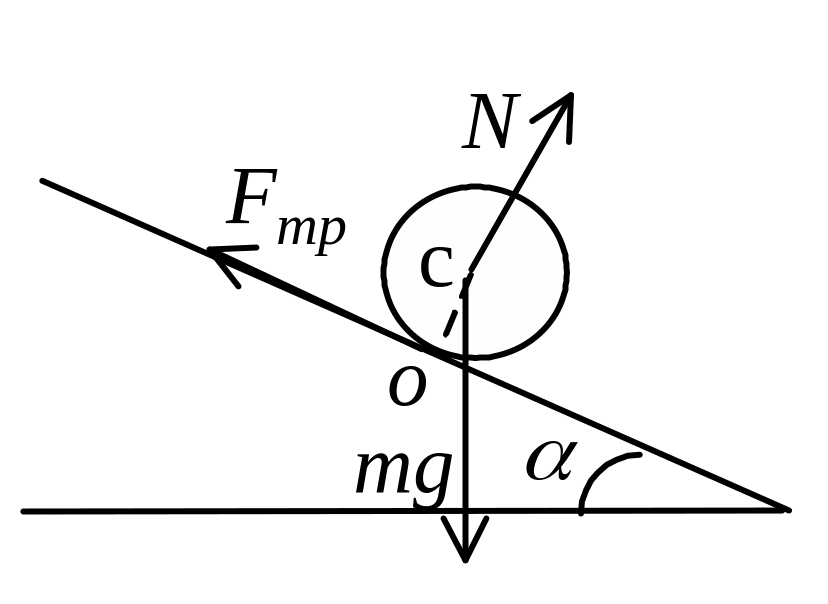 адача
44. По наклонной
плоскости катится круглое тело без
скольжения. Плоскость наклонена к
горизонту под углом a
. Пренебрегая трением качения и
сопротивлением воздуха, определите
ускорение скатывающегося тела. При
каких значениях коэффициента трения m
возможно качение без скольжения ?
адача
44. По наклонной
плоскости катится круглое тело без
скольжения. Плоскость наклонена к
горизонту под углом a
. Пренебрегая трением качения и
сопротивлением воздуха, определите
ускорение скатывающегося тела. При
каких значениях коэффициента трения m
возможно качение без скольжения ?
Решение. Рассмотрим энергетическое решение. Так как тело катится без скольжения, а сопротивлением воздуха и трением качения можно пренебречь, то при движении тела сохраняется его механическая энергия. Вначале тело покоится, и его механическая энергия равна потенциальной энергии mgh, а после скатывания механическая энергия равна сумме кинетической энергии поступательного движения и кинетической энергии вращения:
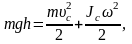 (1)
(1)
где Jc=CmR2 – момент инерции круглого тела относительно оси, проходящей через центр инерции, m – масса тела (С – формпараметр), uс –скорость центра инерции тела, w – угловая скорость вращения тела (R–радиус круглого тела).
Так как тело катится без скольжения, скорость центра инерции uс и угловая скорость вращения тела w связаны соотношением uс=wR (см. задачу 43).
Из уравнения (1) для скорости центра инерции тела uс после скатывания находим
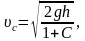 (2)
(2)
где h – высота, с которой скатывается тело.
Центр инерции тела движется с ускорением
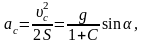 (3)
(3)
так как S=h/sina, uс(0)=0.
Вопрос о значении величины коэффициента трения m энергетически не решается.
Рассмотрим динамическое решение задачи. На тело действует сила тяжести , сила реакции и сила трения покоя (см. рисунок). Под действием этих сил тело вращается и двигается поступательно согласно уравнениям динамики:
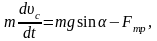 (4)
(4)
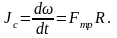 (5)
(5)
Исключая из системы уравнений (4) и (5) силу трения с учетом, что uс=wR и Jc=CmR2, получаем формулу для расчета ускорения центра инерции тела (3).
Рассмотрим вопрос об оценке значения коэффициента трения m .
Выразим из системы уравнений (4) и (5) силу трения
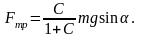
Сила трения покоя ограничена максимальным значением
Fтрmax=mN=mmgsina.
Из условия Fтр£Fтрmax получаем соотношение, ограничивающее значение коэффициента трения
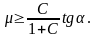
Качение без скольжения для заданного значения коэффициента трения m возможно для углов наклона a, удовлетворяющих условию
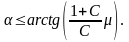
Задача 45. Круглое тело радиусом r катится без скольжения по наклонной плоскости, которая плавно переходит в цилиндрическую поверхность радиусом R. С какой минимальной высоты необходимо скатить тело, чтобы оно могло преодолеть препятствие в форме “мертвой петли“ ? Сопротивлением воздуха и трением качения пренебречь.
Решение. Скорость центра инерции круглого тела в точке А
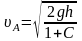
(см. задачу 44).
Движение по внутренней поверхности цилиндра описывается системой уравнений динамики:
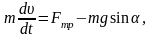 (1)
(1)
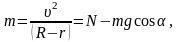 (2)
(2)
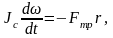 (3)
(3)
где Jc=Cmr2 – момент инерции круглого тела относительно собственной оси вращения (m – масса тела, С – формпараметр).
К уравнениям (1)-(3) следует добавить соотношение, связывающее скорость поступательного движения тела и угловую скорость вращения при отсутствии скольжения:
u=wR. (4)
Из уравнений (1) и (3) с учетом (4) находим уравнение для скорости поступательного движения тела
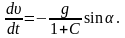
Проинтегрируем последнее уравнение (см. задачу 32), учитывая, что u=uA при j=0.
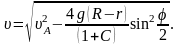 (5)
(5)
Проанализируем физическую ситуацию в критической точке В. Тело должно дойти до точки В и не оторваться от нее.
Из основного уравнения динамики (2)для точки В
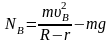
видно, что сила реакции NB определяется скоростью поступательного движения в этой точке. Тело не отрывается в точке В, если NB>0. Минимальную скорость тела в точке В, при которой оно не отрывается от данной точке, оценим, положив NB=0:
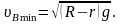 (6)
(6)
Из формулы (5) для минимальной высоты спуска получаем
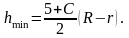
Этот же результат можно получить из энергетических соображений (убедитесь в этом).
Задача 46. Профиль края горизонтального стола скруглен в полуокружность радиусом R. Круглое тело радиусом r катится по столу без скольжения со скоростью u0. Пренебрегая трением качения и сопротивлением воздуха, определите место отрыва тела от поверхности стола и скорость тела в момент отрыва.
Р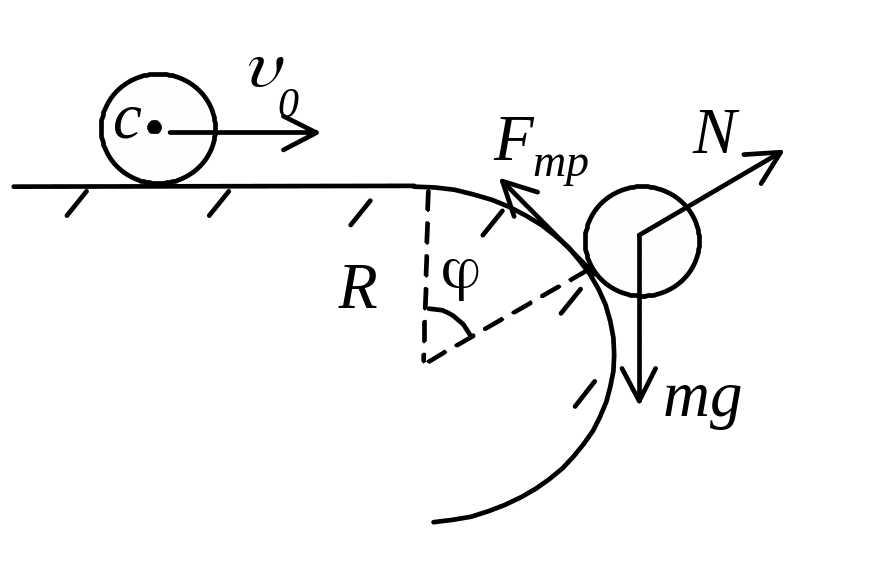 ешение.
При движении
тела по горизонтальной поверхности
стола скорость поступательного движения
и угловая скорость вращения w=u0/r
не изменяются.
ешение.
При движении
тела по горизонтальной поверхности
стола скорость поступательного движения
и угловая скорость вращения w=u0/r
не изменяются.
Движение тела по скруглению описывается уравнениями динамики:
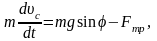 (1)
(1)
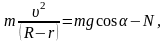 (2)
(2)
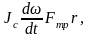 (3)
(3)
где Jc=Cmr2, uc=wr (см. задачи 44, 45).
Решая систему уравнений (1) – (3) с учетом начального условия u=u0 при j=0, находим
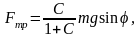
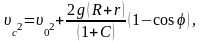
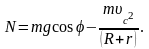
Скорость поступательного движения тела uc увеличивается с ростом полярного угла j, а сила реакции N уменьшается. В точке отрыва N=0. Отсюда получаем соотношение для определения полярного угла, соответствующего точке отрыва:
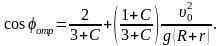
Скорость поступательного движения тела в момент отрыва равна
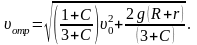
Полученные выражения для joтр и uoтр содержат множество частных случаев (убедитесь в этом).
Интерес представляет проверка предположения о качении без скольжения. Такое качение возможно, если сила трения покоя не превосходит в любой точке максимальной силы трения покоя:
Fтр£mN.
Проведите самостоятельно этот анализ.
Задача 47. Человек, масса которого m1=65кг, переходит с края вращающейся платформы в ее середину. Считая платформу однородным кругом, а человека материальной точкой, оцените изменения кинетической энергии системы. Масса и радиус платформы соответственно равны m2=210 кг, R=2,1м. Начальная угловая скорость вращения системы равна w0=2,3рад/с. Трением в оси платформы и сопротивлением воздуха пренебречь.
Решение. Вопрос: “Будет ли изменяться кинетическая энергия системы?”
Для указанных в условии задачи приближениях систему платформа – человек можно считать изолированной. Поэтому при переходе человека в центр платформы будет сохраняться момент импульса системы относительно оси вращения платформы:
Jw=J0w0,
где J0=J(1+2m1/m2), J=0,5m2R2 – момент инерции платформы относительно собственной оси вращения, w-угловая скорость вращения системы после перехода человека в центр платформы.
Кинетическая же энергия системы при этом не сохраняется. Чтобы сохранялась механическая энергия, одного требования изолированности системы недостаточно. Система взаимодействующих тел должна быть еще и консервативной.
Консервативна ли наша система? Человек имеет возможность передвигаться относительно платформы только благодаря наличию силы трения. Сила трения покоя позволяет мышечной энергии человека превращаться в кинетическую энергию вращения. Наша система неконсервативная. Кинетическая энергия системы возрастает за счет биоэнергии человека. При переходе в центр платформы человек за счет силы энергии покоя “раскручивает” платформу.
Приращение кинетической энергии можно найти, вычислив работу, связанную с переходом человека в центр платформы, или как разницу кинетических энергий системы:
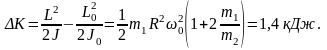
Здесь учтено, что L=L0=J0w0.
Отметим, что человек может передвигаться по платформе, если коэффициент трения удовлетворяет условию m³w02R/g.
Задача 48. На краю вращающейся платформы находится шайба массой m1=0,21кг. К шайбе одним концом привязана нерастяжимая нить, другой конец которой пропущен через небольшое отверстие в центре платформы. С помощью нити шайбу перемещают в центр платформы. Коэффициент трения между шайбой и платформой равен m=0,4. Оцените работу, затраченную на перемещение шайбы, пренебрегая ее размерами, трением в оси платформы и сопротивлением воздуха. Радиус и масса платформы соответственно равны R=0,57м, m2=5,6кг.
Решение. Хотя рассматриваемая система не является изолированной, тем не менее к ней можно применить закон сохранения момента импульса, так как момент силы натяжения нити относительно оси вращения равен нулю. Поэтому можно записать
Jw=J0w0,
где J0=J(1+2 m1/m2), J=0,5m2R2.
Кинетическая энергия системы при этом возрастает на величину (см. задачу 47)
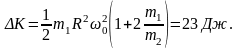
Работа по перемещению шайбы равна сумме приращения кинетической энергии системы и работы силы трения:
A=DK+mmgR=23,5Дж.
Эту же работу можно вычислить непосредственно по формуле работы:
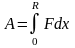 ,
,
где F=mm1g+
m1w2x
– сила, приложенная к нити (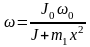 – угловая скорость вращения системы).
– угловая скорость вращения системы).
Задача 49. Человек идет по краю круглой платформы и возвращается в исходную точку. Считая человека точкой, а платформу однородным диском, оцените, на какой угол повернется платформа. Масса человека и платформы соответственно равны m1=75кг, m2=150кг. Трением в оси платформы и сопротивлением воздуха пренебречь.
Решение. При передвижении человека по краю платформы сама платформа с человеком будет вращаться относительно Земли в противоположную сторону движения человека относительно платформы. Для простоты предположим, что человек движется по краю платформы равномерно с угловой скоростью w/ относительно платформы. При этом платформа будет вращаться относительно Земли с угловой скоростью wпл, а человек – с угловой скоростью, равной сумме
w=w/+wпл.
Для определения угла поворота платформы воспользуемся законом сохранения момента импульса:
Jw+J плwпл=0,
где J=m1R2, J пл =0,5m2R2 – моменты инерции человека и платформы.
Откуда для угловой скорости вращения платформы получаем
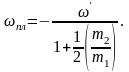
Умножив последнее соотношение на время движения, для угла поворота платформы находим
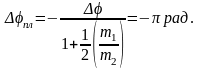
Знак “ – “ указывает на то, что платформа поворачивается в обратную сторону движения человека по краю платформы.
Угол поворота не зависит от характера движения человека по краю платформы.
Задача 50. Однородный стержень массой m=250г и длиной l=1,2м подвешен за один из концов. Небольшое тело массой m0=120г движется горизонтально со скоростью u0=4,2м/с, сталкивается так, что стержень после столкновения отклоняется на максимально возможный угол. Определите место столкновения тела со стержнем (расстояние от точки подвеса до точки столкновения) и угол отклонения стержня, считая столкновение абсолютно упругим, пренебрегая сопротивлением воздуха и трением в оси.
Р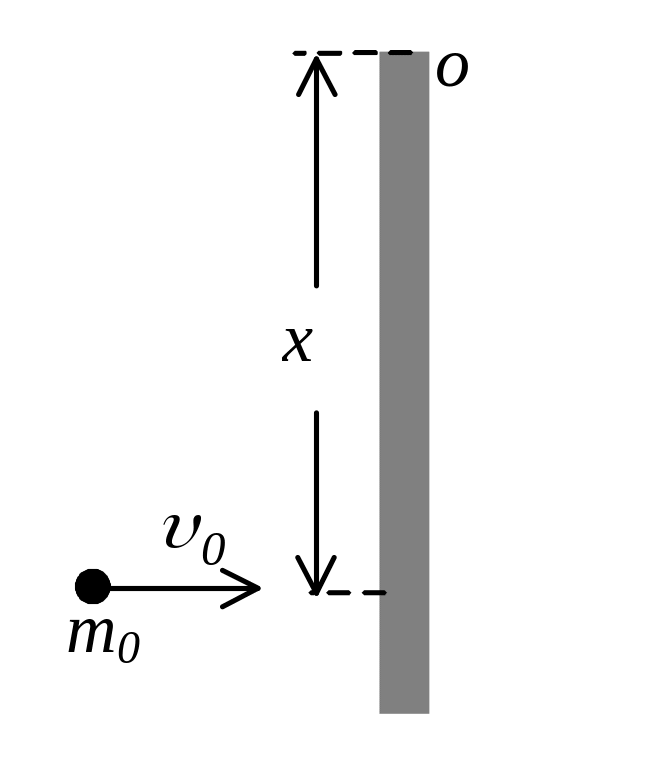 ешение.
Воспользуемся
законом сохранения момента импульса и
механической энергии
ешение.
Воспользуемся
законом сохранения момента импульса и
механической энергии
P0x=L+Px, (1)
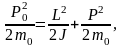 (2)
(2)
где J=(1/3)ml2 – момент инерции стержня относительно точки подвеса, P0=m0u0, P=m0u – импульсы тела до и после столкновения, L – момент импульса стержня после столкновения.
Из уравнений (1) и (2) для неизвестных P и L находим
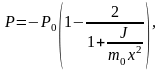 (3)
(3)
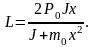 (4)
(4)
Как
видно, значения P
и L зависят от координаты места
столкновения. Функция L(x)
имеет максимум. Из условия экстремума
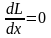 получаем
получаем
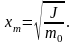
Максимальный момент импульса, который получает стержень при столкновении, равен
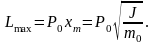
При этом импульс тела после столкновения равен нулю (убедитесь в этом).
Отклонение стержня в однородном поле тяжести Земли после столкновения можно оценить, решая динамическую задачу или используя закон сохранения механической энергии.
Для расчета угла отклонения стержня получается следующее соотношение:
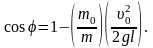
После вычислений получаем xm=1,0 м, j=730.
Задачи для самостоятельного решения (Поступательное и вращательное движения твердого тела)
1. Маховик, масса которого m=5,2кг распределена по ободу, свободно вращается вокруг горизонтальной оси, проходящей через его центр, с частотой 720об/мин. При торможении маховик останавливается через 20с. Определите тормозящий момент, если радиус маховика равен 36см (2,5Нм).
2. На однородный цилиндр массой 5,1кг намотана нерастяжимая нить, к концу которой прикреплен груз массы 0,25кг. В момент времени t=0 система пришла в движение. Определите кинетическую энергию всей системы к моменту времени 3,3с (2Дж).
3. На неподвижный блок намотана нерастяжимая нить, к концу которой прикреплен груз массой 1,7кг. Определите, с каким ускорением будет падать груз, если масса блока равна 2,2кг. Блок считать однородным диском. Сопротивлением воздуха и трением в оси блока пренебречь (6,1м/с2).
4. На неподвижный блок намотана нерастяжимая нить, к концам которой прикреплены грузы массами 1,6кг и 1,2кг. Определите кинетическую энергию системы через 1,8с после начала движения. Масса блока 3,2кг. Блок считать однородным диском. Нить не проскальзывает по блоку. Сопротивлением воздуха и трением в оси пренебречь (15Дж).
5. На неподвижный блок, масса которого равна 25кг, намотана веревка. На веревке висит обезьяна, которая пытается взобраться по ней вверх. С каким ускорением движется веревка, если обезьяна все время остается на одной и той же высоте от пола ? Масса обезьяны 5,0кг. Трением в оси блока и массой веревки можно пренебречь (4,0м/с2).
6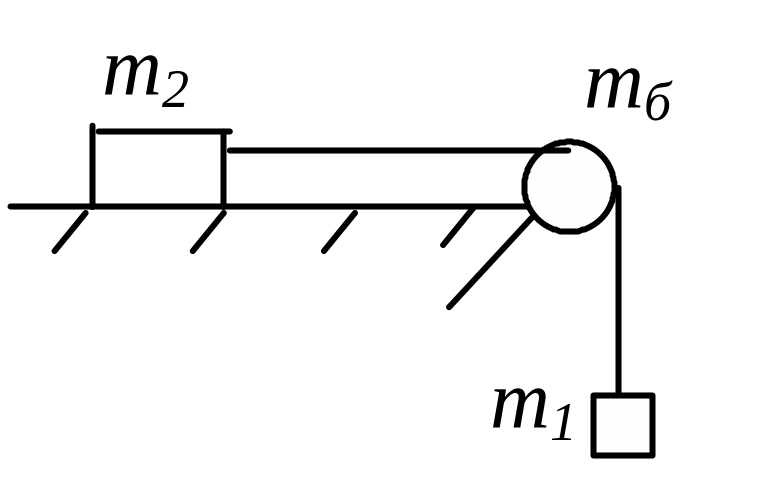 .
Система
тел (см. рисунок) движется с ускорением
1,4м/с2,массы
грузов m2=2,3кг,
mб=1,6кг,
коэффициент трения m=0,2.
Нить
нерастяжима и не проскальзывает по
блоку.
Пренебрегая
сопротивлением воздуха и трением в оси
блока, определите массу m1.
Блок считать однородным диском
(1,0кг).
.
Система
тел (см. рисунок) движется с ускорением
1,4м/с2,массы
грузов m2=2,3кг,
mб=1,6кг,
коэффициент трения m=0,2.
Нить
нерастяжима и не проскальзывает по
блоку.
Пренебрегая
сопротивлением воздуха и трением в оси
блока, определите массу m1.
Блок считать однородным диском
(1,0кг).
7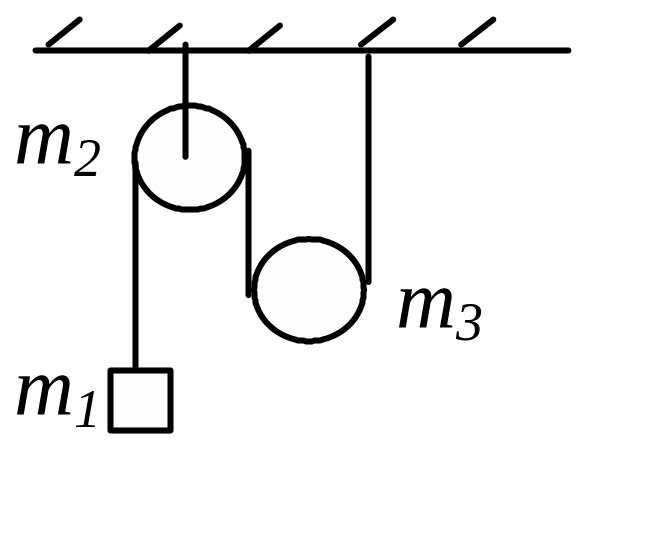 .
Связанная система состоит из трех тел
(см. рисунок): неподвижного блока массой
m2=1,8кг,
подвижного блока массой m3=2,0кг
и груза массой m1=1,5кг.
Определите,
с каким ускорением падает груз, если
нить нерастяжима и не проскальзывает
по блокам
(1,6м/с2).
.
Связанная система состоит из трех тел
(см. рисунок): неподвижного блока массой
m2=1,8кг,
подвижного блока массой m3=2,0кг
и груза массой m1=1,5кг.
Определите,
с каким ускорением падает груз, если
нить нерастяжима и не проскальзывает
по блокам
(1,6м/с2).
8. Хоккейную шайбу раскрутили до угловой скорости 31рад/с и положили плашмя на лед. Определите время торможения шайбы, если масса и радиус шайбы соответственно равны 0,21кг и 3,2см. Коэффициент трения между шайбой и льдом равен 0,13 (0,57с).
9. Шар, вращающийся вокруг собственной оси с частотой 10об/с, поставили на горизонтальную поверхность. Определите угловую скорость качения шара и долю ее начальной кинетической энергии, которая превращается в теплоту (18 рад/с, 71%).
10. Полый тонкостенный цилиндр, вращающийся с угловой скоростью 15рад/с, поставили на горизонтальную поверхность. За какое время цилиндр пройдет расстояние 5,7м, если его радиус равен 12см, а коэффициент трения между цилиндром и горизонтальной поверхностью равен 0,25 (6,6с).
11. Горизонтальная поверхность плавно переходит в плоскую горку с углом наклона a=250 к горизонту. Однородный цилиндр, вращающийся с угловой скоростью 45рад/с, поставили на горизонтальную поверхность вдали от подножия горки. Определите, на какую высоту вкатится цилиндр, если коэффициент трения между цилиндром и поверхностью всюду равен 0,2. Радиус цилиндра равен 13см. Трением качения и сопротивлением воздуха пренебречь (29см).
12. Однородный шар спускается по наклонной плоскости с высоты 1,5м. Угол наклона плоскости к горизонту равен 330. Коэффициент трения между шаром и плоскостью всюду, включая горизонтальную поверхность, равен 0,15. Определите установившуюся скорость качения шара по горизонтальной поверхности, если трением качения и сопротивлением воздуха можно пренебречь (4,5м/с).
13. Однородный цилиндр движется по наклонной плоскости с некоторой высоты без начальной скорости. Плоскость наклонена к горизонту под углом 260. Коэффициент трения между телом и плоскостью равен 0,1. Определите отношение кинетической энергии в конце спуска к начальному значению потенциальной энергии тела. Трением качения и сопротивлением воздуха пренебречь (0,9).
14. С какой минимальной высоты необходимо скатить шарик радиусом r=1,1см, чтобы он смог преодолеть барьер в форме “мертвой петли” радиусом R=13см? Шарик катится без скольжения. Сопротивлением воздуха и трением качения пренебречь (33см).
15. Полый тонкостенный цилиндр катится по горизонтальной поверхности, которая плавно переходит в цилиндрическую, без скольжения. При какой минимальной скорости поступательного движения цилиндр прокатится по цилиндрической поверхности, не выпадая, если радиус цилиндрической поверхности равен 41см, а радиус полого цилиндра 2,0см. Трением качения и сопротивлением воздуха пренебречь (3,4м/с).
16. Наклонная плоскость плавно переходит в цилиндрическую поверхность радиусом R=1,2м. Шарик скатывается без скольжения по наклонной плоскости с высоты 2,5м без начальной скорости. Определите высоту точки отрыва шарика от поверхности цилиндра. Радиус шарика равен 0,15м. Трением качения и сопротивлением воздуха пренебречь (1,9м).
17. Диск катится без скольжения по наклонной плоскости с углом наклона к горизонту 270, плавно переходящей в цилиндрическую поверхность радиусом кривизны 25см. Определите минимальную высоту, с которой необходимо скатить диск, чтобы он оторвался от поверхности на линии перехода наклонной плоскости в цилиндрическую поверхность. Радиус диска равен 5см (0,2м).
18. Шар скатывается без скольжения с вершины сферы радиусом 0,50м с начальной скоростью 1,0м/с. Определите полярный угол, соответствующий месту отрыва шарика от сферической поверхности, если сопротивлением воздуха и трением качения можно пренебречь. Радиус шара 10см (490).
19. Шар скатывается без скольжения по наклонной плоскости, которая плавно переходит в цилиндрическую поверхность радиусом R=1,5м. Радиус шара r=11см. Шар скатывается с высоты h=2,9м без начальной скорости. Определите координату точки отрыва шара от поверхности цилиндра ( полярный угол ) (1300).
20. На однородный стержень, подвешенный за один из концов, попадает горизонтально летящее тело и прилипает к нему. Определите, на какой угол отклоняется стержень от вертикального положения. Длина и масса стержня соответственно равны 0,51см, 980г. Масса тела 12г. Расстояние от точки подвеса до линии движения тела равно 34см. Скорость тела до столкновения 30м/с (150).
21. Шар массой 2,1кг подвешен на легком стержне. В шар попадает горизонтально летящая пуля массой 9,0г и застревает в середине шара. Определите скорость пули, если система отклонилась от положения равновесия на угол 400.Длина стержня и радиус шара соответственно равны 6,5см, 35см. Сопротивлением воздуха и трением в оси подвеса пренебречь (520 м/с).
22. Период вращения Солнца вокруг собственной оси равен 27 земным суткам. Солнце представляет собой водородную звезду. После того как полностью выгорит водород, Солнце испытает гравитационный коллапс. Оцените радиус Солнца, прежде чем оно разлетится на части. Масса Солнца 2,0×1030 кг, радиус Солнца 7,0×108 (14км).
Примеры решения задач (Колебательное движение)
Задача 51. Максимальная частота колебаний физического маятника массой m=2,3кг равна nmax=1,3Гц. Определите момент инерции маятника относительно оси, проходящей через ее центр инерции.
Р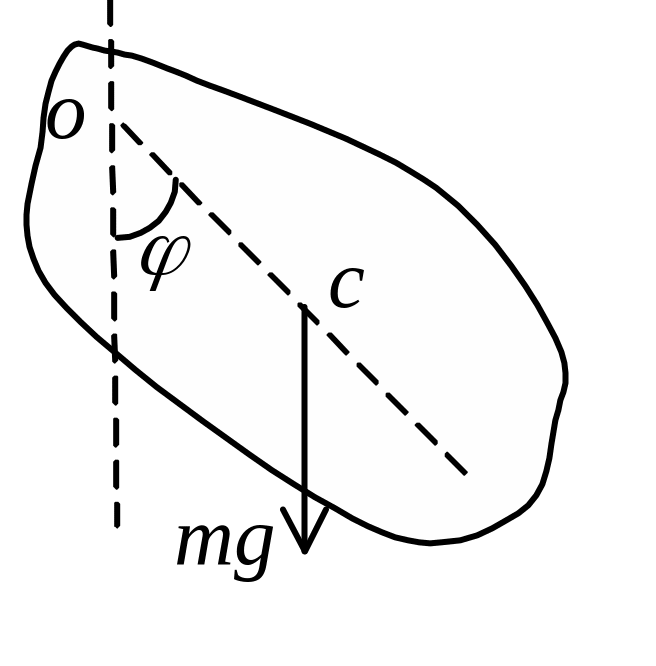 ешение.
Маятник совершает вращательное
колебательное движение относительно
оси качания под действием момента силы
тяжести
ешение.
Маятник совершает вращательное
колебательное движение относительно
оси качания под действием момента силы
тяжести
Jo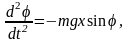
где x=ОС, J0=Jc+mx2, Jc – момент инерции маятника относительно оси, проходящей через центр инерции С, m – масса маятника.
В таком приближение мы пренебрегаем сопротивлением воздуха и трением в оси качания маятника.
При малых углах отклонения маятник совершает гармоническое колебательное движение с угловой частотой
w=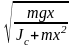 .
.
Зависимость угловой частоты от положения оси качания w(x) имеет максимум при
хm=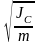 .
.
Максимальная угловая частота равна
wmax=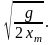
Откуда находим
Jc=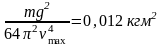 .
.
Физический маятник применяется для измерения ускорения свободного падения.
Задача 52. По внутренней поверхности цилиндра радиусом R катается круглое тело без проскальзывания. Определите период малых колебаний тела около положения равновесия. Радиус круглого тела равен r. Сопротивлением воздуха и трением качения пренебречь.
Решение. Рассмотрим динамическое решение задачи.
П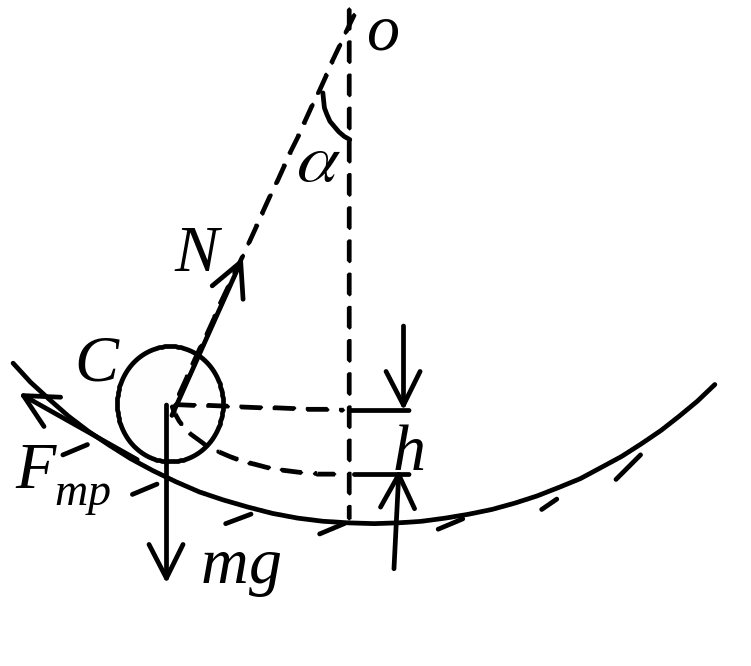 оступательное
и вращательное движения тела под
действием сил тяжести, реакции и трения
(см. рисунок) описываются основными
уравнениями динамики твердого тела
оступательное
и вращательное движения тела под
действием сил тяжести, реакции и трения
(см. рисунок) описываются основными
уравнениями динамики твердого тела
Fтр-mgsin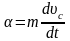 , (1)
, (1)
-Fтр×r=Jc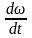 , (2)
, (2)
где Jc=cmr2 – момент инерции круглого тела относительно собственной оси вращения.
Из уравнений (1) и (2), учитывая, что uс=wr (отсутствие проскальзывания), для ускорения поступательного движения тела получаем следующее уравнение:
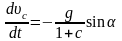 .
.
Откуда при малых углах для смещения S=(R-r) находим
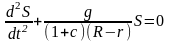 .
.
Таким образом, смещение S(t) описывается гармонической функцией с угловой частотой
w=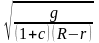
и периодом колебаний
T=2П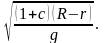
Этот же результат можно получить из закона сохранения механической энергии:
mgh=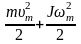 ,
,
где h – высота, с которой скатывается тело, J=(1+c)mR2 – собственный момент инерции тела, um,wm – линейная скорость поступательного и угловая скорость вращательного движений тела при прохождении положения равновесия. Учитывая соотношение um =wmR, выразим скорость поступательного движения тела при прохождении положения равновесия:
um=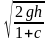 .
.
Для малых угловых смещений высота h геометрически связана с максимальным смещением центра инерции тела Sm и R-r соотношением
h=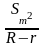 .
.
Максимальная скорость гармонических колебаний пропорциональна амплитуде:
um=wSm.
Следовательно, частота гармонических колебаний равна
w= .
Качение без скольжения возможно, если
m³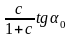 ,
,
где a0 - полярный угол, соответствующий максимальному отклонению от положения равновесия. Исследуйте самостоятельно эту проблему.
Задача 53. На гладкой горизонтальной поверхности находятся два тела, связанные легкой пружиной жесткостью к=95Н/м. Определите частоту колебаний системы, если масса тел m1=0,86кг и m2=0,34кг.
Решение. Тела находятся под действием упругой силы, пропорциональной величине деформации пружины:
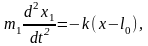 (1)
(1)
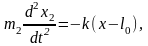 (2)
(2)
где x=x1 +x2 – длина пружины, x1 и x2 – смещение тел относительно центра инерции системы, l0 – длина недеформированной пружины.
Из уравнений (1) и (2) находим
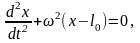
где
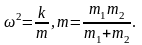
Расстояние между телами изменяется по гармоническому закону с частотой
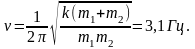
Задача 54. Однородный брусок положили на два вращающихся навстречу друг другу ролика (см. рисунок). Расстояние между осями роликов l=85см, коэффициент трения между бруском и роликами m=0,35. Как будет двигаться брусок?
Р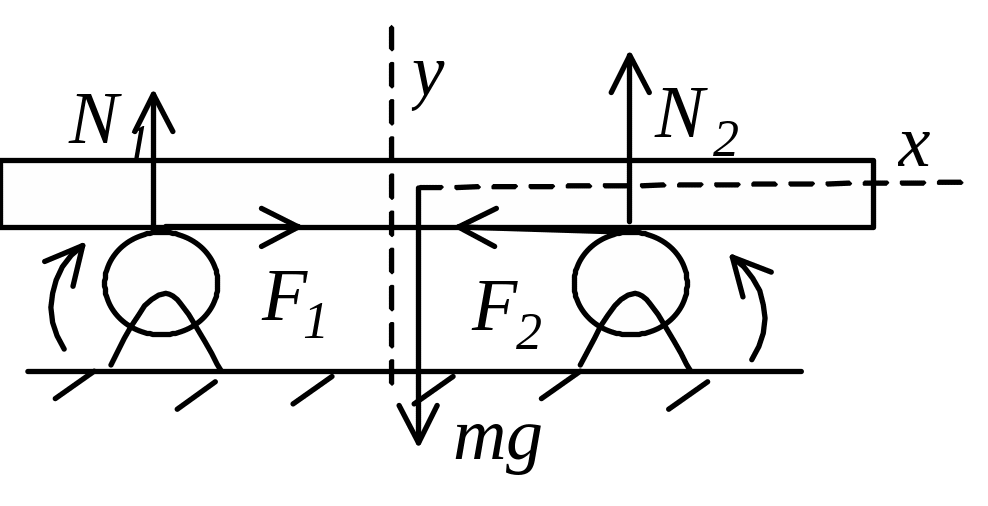 ешение.
Состояние бруска, находящегося под
действием сил, указанных на рисунке,
описывается системой уравнений:
ешение.
Состояние бруска, находящегося под
действием сил, указанных на рисунке,
описывается системой уравнений:
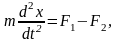 (1)
(1)
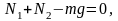 (2)
(2)
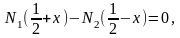 (3)
(3)
где F1=mN1, F2 =mN2, m – масса бруска, x -– смещение центра инерции бруска от положения равновесия.
Из совокупности уравнений (1)–(3) следует, что движение бруска по оси ох описывается уравнением
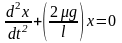 .
.
Следовательно, брусок совершает гармонические колебания с угловой частотой
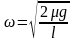
и периодом
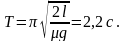
Отметим, что частота и период колебаний не зависят от массы бруска. Как это объяснить?
Задача 55. Какое движение совершает небольшое тело, свалившееся в радиальную шахту, прорытую сквозь астероид. Астероид принять однородным шаром с плотностью r =6,0г/см3.
Решение. Эта абстрактная задача интересна тем, что позволяет выяснить особенности движения тел в гравитационном поле сферически симметричного тела и использовать их при решении других проблем движения тел в гравитационных полях.
Начало координат свяжем с геометрическим центром астероида. При этом ускорение свободного падения тела в шахте будет зависеть от расстояния до центра астероида. Найдем эту зависимость а(r).
Сила тяжести, действующая на тело в шахте, определяется только массой, ограниченной сферой радиусом r, m=(4/3)pr3r (почему?)
Поэтому
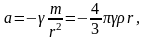
т.е. тело, упавшее в шахту, будет совершать гармоническое колебательное движение с угловой частотой
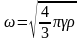
и периодом
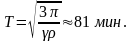
Период гармонических колебаний тела в шахте не зависит от размера астероида и определяется только его плотностью.
Найдем иное соотношение для периода гармонических колебаний тела в шахте. Для этого воспользуемся выражением для плотности однородного астероида и ускорения свободного падения тел у поверхности астероида:
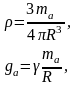
где ma, R- масса и радиус астероида.
Период гармонических колебаний тела в шахте определяется радиусом астероида и ускорением падения тел у поверхности астероида:
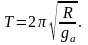
Обратите внимание на аналогию с математическим маятником.
Расстояние тела от центра астероида и скорость изменяются по гармоническому закону:
r=Rcoswt,
u= - wRsinwt.
При прохождении центра скорость тела будет максимальной:
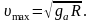
Но это, с другой стороны, первая космическая скорость для астероида.
Найдем период обращения спутника астероида, круговая орбита которого проходит вблизи его поверхности:
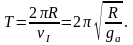
Удивительно, для двух разных движений в поле тяготения, обладающего свойством сферической симметрии, получается один и тот же результат! Случайно ли это ?
Нельзя ли воспользоваться полученным результатом для решения иных задач ? Например, для оценки времени падения Луны на Землю, если бы она вдруг потеряла свою орбитальную скорость в результате космической катастрофы. Подумайте над этим.
Задача 56. Небольшое тело начинает скользить по горизонтальной поверхности с начальной скоростью u0=13м/с. Коэффициент трения скольжения зависит от пройденного пути по закону m=bS, где b=0,431/м. Определите путь, пройденный телом до остановки, и время торможения. Сопротивлением воздуха пренебречь.
Решение. Проанализируем физическую ситуацию. Вначале воспользуемся методом анализа размерностей. Выделим характерные величины, определяющие процесс торможения: [u0]=м/с – начальная скорость тела, [g]=м/с2 – ускорение силы тяжести, [b]=1/м – коэффициент, характеризующий силу трения скольжения.
Из этих величин можно составить единственную комбинацию, которая имеет размерность длины:
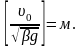
Следовательно, тормозной путь пропорционален указанной комбинации характерных величин
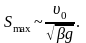
Очевидно, для оценки времени торможения можно воспользоваться соотношением
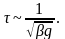
Т еперь рассмотрим проблему более детально. Тело тормозится под действием силы трения Fтр=-mN. В нашем случае N=mg, m=bS. Сила трения возрастает по линейному закону от пройденного пути и направлена в обратную сторону движения, т. е. выполняет роль квазиупругой силы:
F тр= -mw2S,
где
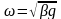 .
.
Откуда следует, что тело движется до остановки, подчиняясь гармоническому закону с круговой частотой w .
Динамически движение тела сводится к решению уравнения
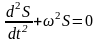
с начальными условиями S(0)=0, u(0)=u0.
Пройденный путь изменяется с течением времени по гармоническому закону
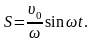
Положив sinwt=1, для тормозного пути и времени торможения получаем
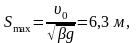
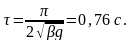
Заметим, что тормозной путь можно также найти из энергетических соображений, воспользовавшись теоремой о кинетической энергии: DK=Aтр.
Задача 57. Круглое тело массой m(кг) лежит на горизонтальной поверхности. К оси тела прикреплена одним концом легкая пружина жесткостью К(Н/м), другой конец которой прикреплен к неподвижной стенке (см. рисунок). Тело сместили от положения равновесия на величину x0(м) и отпустили в момент времени t=0. Определите период колебаний тела, если качение происходит без скольжения. Сопротивлением воздуха и трением качения пренебречь.
Р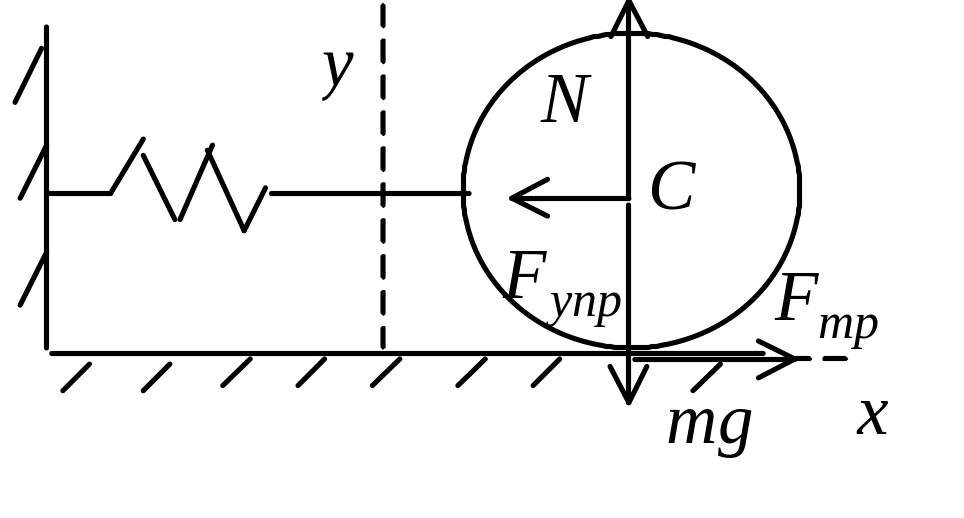 ешение.
Рассмотрим динамическое решение задачи.
ешение.
Рассмотрим динамическое решение задачи.
Под действием указанных на рисунке сил тело движется поступательно и вращается вокруг собственной оси в соответствии с основными уравнениями динамики:
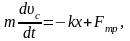 (1)
(1)
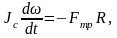 (2)
(2)
где Jс=CmR2 – момент инерции круглого тела относительно собственной оси вращения, проходящей через центр инерции (С – формпараметр круглого тела), m – масса тела, uc – скорость поступательного движения центра инерции тела, w – угловая скорость вращения.
В отсутствие проскальзывания (uc=wR) поступательное движение тела описывается уравнением
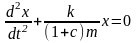
с начальными условиями x(0)=x0, u(0)=0.
Поступательному движению соответствует гармоническое колебание
x=x0coswt
с круговой частотой
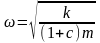
и периодом колебаний
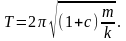
Качение без скольжения возможно, если коэффициент трения удовлетворяет условию
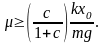
Обоснуйте это утверждение.
Вычислите период колебаний для цилиндра массой m=1,6кг, если k=125Н/м.
Задача 58. На горизонтальной поверхности с коэффициентом трения m=0,12 лежит брусок массой m=0,60кг, прикрепленный к стенке легкой пружиной жесткостью k=2,5Н/см. Брусок сместили так, что пружина растянулась на x0 =9,5см, и затем отпустили. Определите число колебаний, которое совершит брусок до остановки. Сопротивлением воздуха пренебречь.
Решение. Вначале проведем качественный анализ физической ситуации.
Е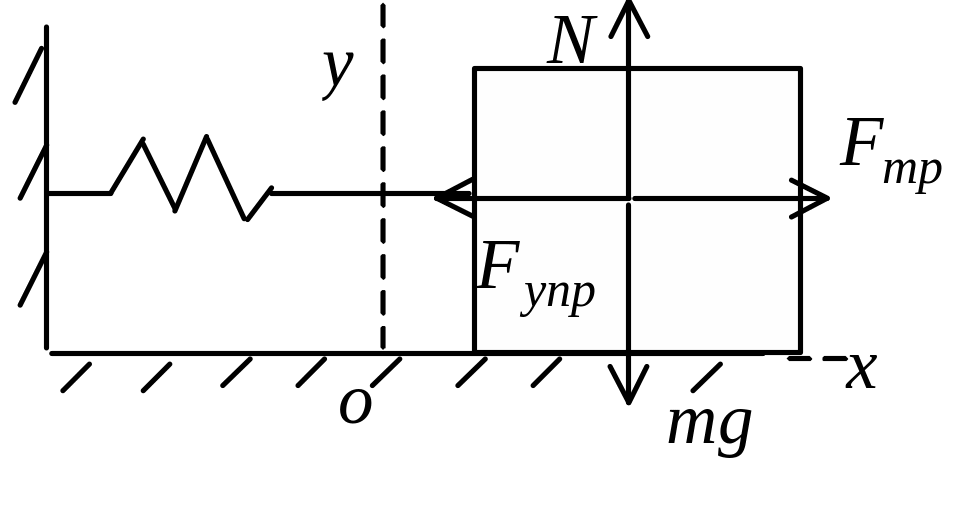 сли
бы сила трения была равна нулю, то тело
под действием упругой силы совершало
бы гармоническое колебательное движение
с угловой частотой
сли
бы сила трения была равна нулю, то тело
под действием упругой силы совершало
бы гармоническое колебательное движение
с угловой частотой
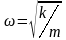 и амплитудой x0.
и амплитудой x0.
Постоянная
сила трения Fтр=mmg
уменьшает амплитуду колебаний, не
изменяя ее частоты. В конце концов тело
остановится на расстоянии
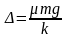 от положения равновесия (почему?).
от положения равновесия (почему?).
Рассмотрим динамическое решение задачи.
Под действием указанных на рисунке сил тело движется поступательно в соответствии с основным законом динамики:
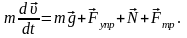
После известных преобразований проблема сводится к решению одномерного дифференциального уравнения
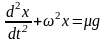
с начальными условиями x(0)=0, u(0)=0.
Поступательное движение тела происходит в соответствии с уравнением движения:
x=D+(x0-D)coswt.
Скорость тела является функцией времени:
u=-w(x0-D)sinwt.
Скорость тела равна нулю для моментов времени, удовлетворяющих условию
wt=np,
где n=0,1,2,…
Ближайший момент времени от начала движения, когда тело останавливается (n=1), равен t=T/2, где Т – период колебаний.
Таким образом, через полпериода смещение равно
x1=D+(x0-D)cosp=-x0+2D.
Откуда видно, что амплитуда уменьшается на 2D через полпериода и на 4D за период. Общее изменение амплитуды за все время движения равно x0-D.
Полное число колебаний до остановки, очевидно, равно
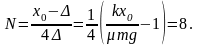
Из решения следует, что колебательное движение возможно, если величина коэффициента трения скольжения удовлетворяет условию
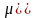
Задача 59. К легкой пружине жесткостью k=25Н/м подвешен шарик радиусом R=2,3см и массой m=120г. Шарик погружен в жидкость. В положении равновесия шарику сообщили начальную скорость u0=1,4м/с в вертикальном направлении. Определите период затухающих колебаний шарика и вязкость жидкости, если логарифмический декремент затухания равен l=3,0.
Решение.
На шарик действуют сила тяжести
,
выталкивающая сила Архимеда
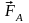 ,
упругая сила пружины
,
упругая сила пружины
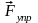 ,сила
вязкого трения
и
сила сопротивления
.
При небольших скоростях Fтр>>Fc
,так как Fтр~u,
а Fc~u2.
,сила
вязкого трения
и
сила сопротивления
.
При небольших скоростях Fтр>>Fc
,так как Fтр~u,
а Fc~u2.
Шарик совершает одномерное движение в вертикальном направлении в соответствии с динамическим уравнением
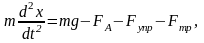 (1)
(1)
г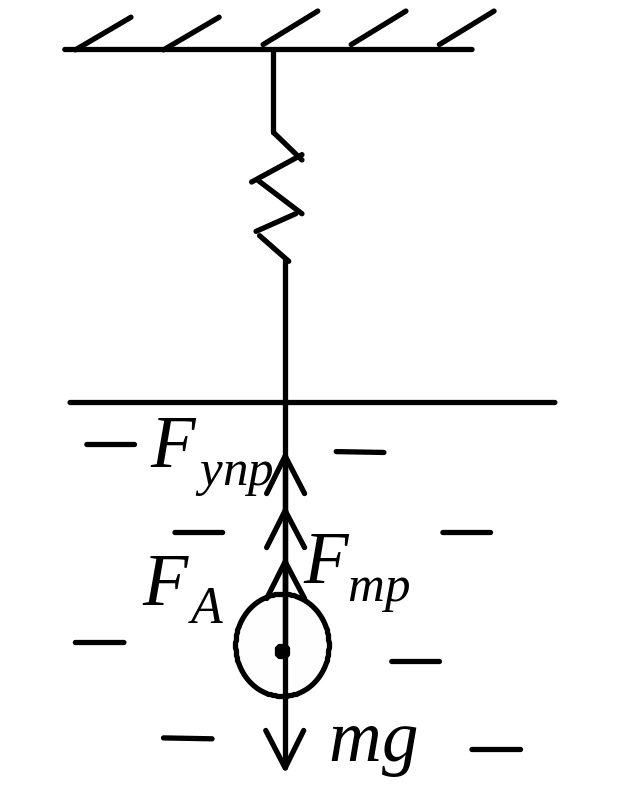 де
Fтр=6phRu
(закон Стокса), Fупр=
-kx (закон
Гука), x
– деформация пружины.
де
Fтр=6phRu
(закон Стокса), Fупр=
-kx (закон
Гука), x
– деформация пружины.
Шарик будет совершать колебательное движение около положения равновесия x0, определяемого равенством
kx0=mg-FA.
Введем
смещение S=x-x0
и комбинированные параметры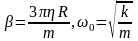 с одинаковыми
размерностями [b]=[w0]=c-1.
с одинаковыми
размерностями [b]=[w0]=c-1.
Окончательно задача сводится к решению уравнения
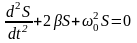
с начальными условиями S(0)=0, u(0)=u0.
Это уравнение затухающих колебаний имеет решение для указанных начальных условий вида
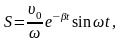
где
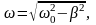 если выполнено условие w02>b2.
если выполнено условие w02>b2.
Декремент затухания определяется отношением амплитуд, разделенных промежутком времени, равным периоду
а![]() логарифмический декремент затухания
равен
логарифмический декремент затухания
равен
l=lnd=bT=2pb/w.
Откуда после несложных преобразований находим расчетное соотношение для вязкости жидкости:
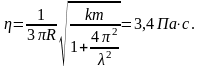
Из решения видно, что начальное значение амплитуды равно
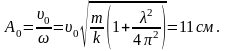
Задача 60. Ось подвеса физического маятника движется под действием внешней силы в горизонтальном направлении по закону x(t)=x0sinwt. Найти установившиеся вынужденные колебания маятника.
Р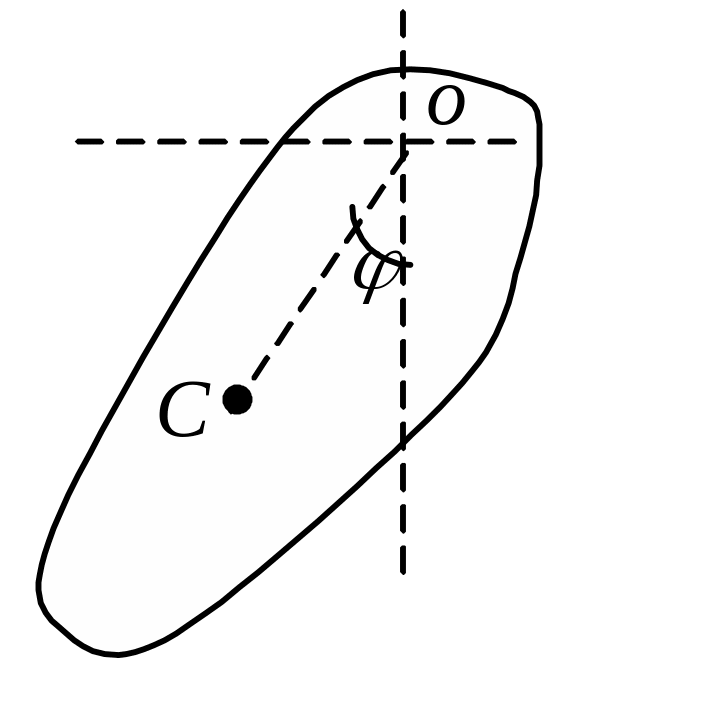 ешение.
Задача состоит в нахождении установившихся
вынужденных колебаний маятника, когда
переходный процесс уже закончился.
Очевидно, что вынужденные колебания
будут происходить с частотой вынуждающей
силы w,
в то время как частота свободных колебаний
маятника равна
ешение.
Задача состоит в нахождении установившихся
вынужденных колебаний маятника, когда
переходный процесс уже закончился.
Очевидно, что вынужденные колебания
будут происходить с частотой вынуждающей
силы w,
в то время как частота свободных колебаний
маятника равна
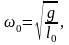
где
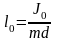 – приведенная длина физического
маятника, J0
– момент инерции физического маятника
относительно оси колебаний, m
– масса маятника, d
– расстояние от оси вращения до центра
инерции тела.
– приведенная длина физического
маятника, J0
– момент инерции физического маятника
относительно оси колебаний, m
– масса маятника, d
– расстояние от оси вращения до центра
инерции тела.
Основная идея решения заключается в том, чтобы представить вынужденные колебания данного маятника как свободные колебания некоторого другого условного маятника с приведенной длиной l:
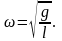
Если 1)w<w0, то l>l0 , 2) w>w0, то l<l0 .
В первом случае при малых колебаниях точки подвеса 0 согласно уравнению
x=x0sinwt
точка А, соответствующая концу приведенной длины условного физического маятника, движется согласно уравнению
x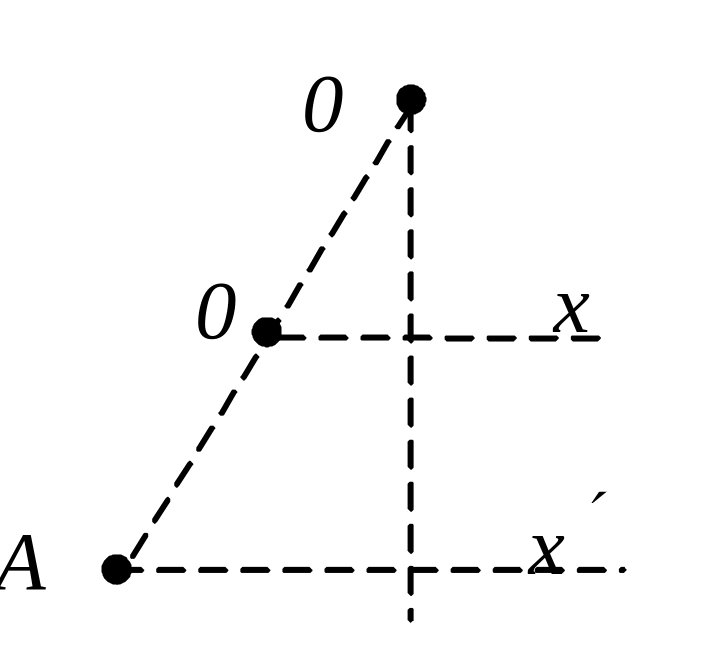 /=x0/sinwt.
/=x0/sinwt.
Таким образом, вынужденное колебание происходит в той же фазе, что и движение точки подвеса 0, а амплитуду этого колебания x0/ можно легко найти из условия геометрического подобия:
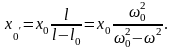
Заметим, что при w®w0 x0/®¥, т. е. наступает резонанс. Вблизи резонанса полученное решение неприменимо, так как мы исходим из предположения о малости колебаний и пренебрегаем сопротивлением, ибо только при учете затухания амплитуда в резонансе получается конечной.
Во втором случае (l<l0), рассуждая аналогично предыдущему случаю, легко прийти к выводу, что движение точки А условного маятника происходит в противофазе с движением точки подвеса 0.
Приведем окончательный результат: вынужденное установившееся колебание физического маятника описывается уравнением
x/=x0/sin(wt+j),
где
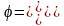
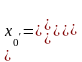
Этот же результат можно получить, решая формально динамическое уравнение вынужденных колебаний (убедитесь в этом)
x//+w02x=x0sinwt.
Задачи для самостоятельного решения (Колебательное движение)
1. Ртуть объемом V=55см3 налита в изогнутую U-образную трубку сечением S=5,1см2. Пренебрегая вязкостью, определите период малых колебаний ртути (0,46с).
2. Определите период малых колебаний ареометра, которому сообщили небольшой толчок в вертикальном направлении. Масса ареометра m=50г, радиус его трубки r=3,0мм, плотность жидкости r=0,8г/см3. Вязкостью жидкости пренебречь (3,0c).
3. Доска длиной l=2,5м движется со скоростью u0=3,2м/с по гладкой горизонтальной полуплоскости, переходящей в полуплоскость с коэффициентом трения m=0,25. Определите путь, пройденный передней кромкой доски за время ее движения по второй полуплоскости, и время торможения (3,3м; 1,9с).
4. Однородный шнур длиной l=2,0м движется по гладкой горизонтальной поверхности, которая плавно переходит в наклонную плоскость с углом наклона a=300. Передний конец шнура остановился на высоте h=80см. Определите время подъема шнура и его начальную скорость (1,0с; 2,5м/с).
5. Лыжник съезжает без начальной скорости по склону холма по прямой, составляющей некоторый угол с горизонтом, и, проехав путь S0=40м, останавливается. Условия движения лыжника таковы, что сила сопротивления, действующая на лыжника со стороны снега, пропорциональна пройденному пути к×S, где к=6,3Н/м. Определите максимальную скорость лыжника при спуске, если его масса m=70кг (6,0м/с).
6. Однородный стержень подвешен так, что его период малых колебаний имеет минимальное значение. Определите приведенную длину этого физического маятника, если длина стержня 48см (14см).
7. Вблизи поверхности Земли имеется полость, заполненная водой (подземное озеро). Оцените размеры этого озера, считая полость шаром радиусом r, если период малых колебаний физического маятника увеличивается в этом месте на 0,01%. Радиус и среднюю плотность Земли принять равными R=6400км, r=6,0г/см3 (r=1,5км).
8. Вблизи поверхности Земли находится рудное месторождение. Оцените объем месторождения, считая его однородным шаром плотностью 8,0г/см3, если период колебаний секундного физического маятника вблизи месторождения уменьшается до 0,998с. Ускорение свободного падения вблизи поверхности и среднюю плотность Земли принять равными 10м/с2 и 6,0г/см3 (1,4×106 км3).
9. Максимальная частота колебаний физического маятника равна 1,3Гц. Определите момент инерции маятника относительно оси, проходящей через ее центр инерции, если его масса равна 2,3кг (0,013кгм2).
10. Между двумя телами массами 1,0кг и 0,6кг зажата легкая пружина жесткостью 100Н/м. Длина пружины в недеформированном состояние равна 10см. При длине пружины 8,0см система тел приходит в движение. Определите скорости тел после того, как пружина распрямится, если вначале она была сжата до 5,0см (0,13м/с; 0,38м/с).
11. Небольшое тело начинает скользить по наклонной плоскости, составляющей угол 350 с горизонтом. Коэффициент трения скольжения зависит от пройденного пути S согласно соотношению m=bS, где b=0,511/м. Определите путь, пройденный телом до остановки, и его максимальную скорость на этом пути (2,7м; 28м/с).
12. Горизонтальная подставка может совершать гармонические колебания с частотой 2,5Гц в вертикальном направлении. При какой минимальной амплитуде колебаний подставки монета, лежащая на подставке, отделяется от нее (4,0см).
13. Горизонтальная площадка совершает гармонические колебания в горизонтальном направлении с частотой 1,6Гц. При какой минимальной амплитуде колебаний тело, лежащее на площадке, будет смещаться относительно площадки, если коэффициент трения между телом и площадкой равен 0,35 (3,5см).
14. Амплитуда затухающих колебаний осциллятора за время t уменьшилась в 1,4 раза. Как за это время изменилась механическая энергии осциллятора ? (уменьшилась в 2 раза).
15. Осциллятор совершает гармонические колебания согласно уравнению x(cм)=5,2sin(53t) под действием вынуждающей силы F(H)=10,2cos(53t). Определите коэффициент затухания осциллятора, если его масса равна 0,23кг (8,01/с).
16. Определите резонансную амплитуду осциллятора, совершающего установившиеся колебания под действием гармонической силы с амплитудой F0=5,7H, если частота затухающих колебаний данного осциллятора w=1401/c и коэффициент сопротивления г=0,35кг/с (12см).
17. Амплитуды вынужденных гармонических колебаний осциллятора при частотах 801/с с 1201/с равны между собой. Определите частоту собственных колебаний осциллятора, если частота его затухающих колебаний равна 1061/с (1101/с).
18. Тело массой 0,12кг, подвешенное на невесомой пружине, совершает вынужденные колебания под действием гармонической силы частотой w=6,31/с и амплитудой F0=12H. Определите среднюю за период механическую энергию осциллятора, если коэффициент упругости пружины равен 78Н/м (1,1Дж).
19. К невесомой пружине подвесили груз, и она растянулась на Dx=4,9см. Определите циклическую частоту затухающих колебаний груза, если ему сообщили небольшой импульс в вертикальном направлении. Логарифмический декремент затухания равен l=1,5 (141/c).
20. На горизонтальной поверхности лежит брусок массой m=0,48кг, соединенный легкой недеформированной пружиной со стеной. Брусок сместили так, что пружина растянулась на x0=4,5см, и отпустили. Совершив 5 полных колебаний, брусок остановился. Определите коэффициент трения между бруском и поверхностью (0,2).
21. Тело, упавшее в радиальную шахту астероида, вернулось обратно через 90мин. Оцените плотность вещества астероида (4,8г/см3).
22. Шар лежит на горизонтальной поверхности. К оси шара прикреплена одним концом легкая пружина, другой конец которой прикреплен к стенке. Шар сместили от положения равновесия на x0=5,7см и отпустили. Оцените, при каких значениях коэффициента трения шар будет кататься без скольжения, совершая гармонические колебания с угловой частотой n=8,31/c (m³0,16).
23. По внутренней поверхности цилиндра радиусом R=95см катается круглое тело без скольжения, совершая гармонические колебания с угловой частотой n=6,11/c. Определите формпараметр круглого тела, если его радиус r=5,0 см (0,7).
24. На гладкой горизонтальной поверхности находятся два тела с массами 0,5кг и 2,0кг, связанные легкой пружиной. Определите жесткость пружины, если система грузов колеблется с частотой 5,0Гц (0,39кН/м).
2 5.
Четыре невесомых стержня длиной l=18см
каждый соединены шарнирно и образуют
квадрат (см. рисунок). Шарниры Д и В
соединены легкой пружиной, которая в
недеформированном состоянии имеет
длину l0
=32см.
Определите частоту малых вертикальных
колебаний груза. Сопротивлением воздуха
и трением в шарнирах пренебречь (1,1Гц).
5.
Четыре невесомых стержня длиной l=18см
каждый соединены шарнирно и образуют
квадрат (см. рисунок). Шарниры Д и В
соединены легкой пружиной, которая в
недеформированном состоянии имеет
длину l0
=32см.
Определите частоту малых вертикальных
колебаний груза. Сопротивлением воздуха
и трением в шарнирах пренебречь (1,1Гц).
