
- •Физика в задачах Механика
- •Предисловие
- •1. Кинематика Основные понятия, соотношения, формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •2. Динамика Основные понятия, соотношения, законы
- •Примеры решения задач (Поступательное движение твердого тела)
- •Задачи для самостоятельного решения (Поступательное движение твердого тела)
- •3.Законы сохранения Примеры решения задач
- •Задачи для самостоятельного решения (Законы сохранения)
2. Динамика Основные понятия, соотношения, законы
Динамика материальной точки
Импульс (количество движения) – векторная мера механического движения частицы:
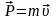 ,
,
где
– скорость частицы,
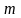 – “инертная” масса частицы.
– “инертная” масса частицы.
Кинетическая энергия – скалярная мера механического движения:
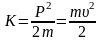 .
.
Момент импульса относительно точки – векторная мера вращательного движения:
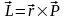 ,
,
где
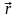 – радиус – вектор частицы относительно
точки.
– радиус – вектор частицы относительно
точки.
Понятие силы и момента силы относительно точки:
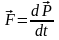 ,
,
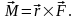
Основное уравнение динамики (второй закон Ньютона):
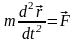 ,
,
где
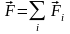 – равнодействующая сил, действующих
на частицу.
– равнодействующая сил, действующих
на частицу.
Основное уравнение динамики в проекциях на касательную и нормаль к траектории:
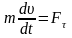 ,
,
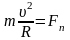 ,
,
где R – радиус кривизны траектории.
Импульс силы, характеризующий действие силы во времени, равен приращению импульса частицы за время действия силы (основной закон динамики в интегральной форме):
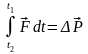 .
.
Работа силы, характеризующая действие силы в пространстве, равна приращению кинетической энергии (теорема о кинетической энергии):
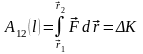 .
.
Мгновенная мощность силы
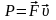 .
.
Средняя мощность (равна отношению работы, совершаемой за промежуток времени Dt, к этому промежутку)
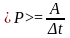 .
.
Частица в потенциальном поле
Энергия частицы в потенциальном поле сохраняется:
Е=К+П=const,
где П – потенциальная энергия частицы в потенциальном поле.
Потенциальная энергия частицы (тела) в поле тяжести Земли
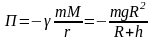 ,
,
где
m
– масса
частицы, R
– радиус
Земли, h
– высота над поверхностью Земли,
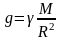 –
ускорение свободного падения у поверхности
Земли.
–
ускорение свободного падения у поверхности
Земли.
Для h<<R
П=mgh – mgR.
Работа сил поля
A=DK=- DП.
Связь между силой и потенциальной энергией частицы в поле:
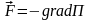 ,
,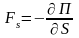 .
.
Уравнение динамики тела переменной массы:
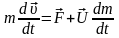 ,
,
где
m
– переменная масса тела,
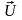 –
скорость отделяемого (присоединяемого)
вещества относительно рассматриваемого
тела,
–
скорость отделяемого (присоединяемого)
вещества относительно рассматриваемого
тела,
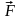 –
сумма внешних сил.
–
сумма внешних сил.
Динамика системы частиц
Импульс системы частиц
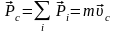 ,
,
где
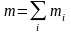 – масса системы частиц (закон аддитивности
массы),
– масса системы частиц (закон аддитивности
массы),
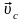 – скорость центра инерции системы
частиц.
– скорость центра инерции системы
частиц.
Уравнение движения центра инерции системы:
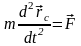 ,
,
где
– результирующая внешних сил,
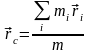 – центр инерции системы.
– центр инерции системы.
Приращение импульса системы частиц
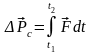 .
.
Импульс изолированной системы частиц сохраняется:
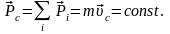
Механическая энергия системы
E=K+П,
где
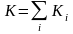 –
кинетическая энергия системы,
–
кинетическая энергия системы,
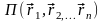 –
потенциальная энергия системы.
–
потенциальная энергия системы.
Изменение механической энергии системы
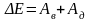 ,
,
где Ав – работа внешних сил, Ад – работа внутренних непотенциальных сил.
Механическая энергия изолированной и консервативной системы сохраняется:
Е=К+П=const, или DК=-DП.
Если
система находится во внешнем потенциальном
поле, то можно ввести понятие потенциальной
энергии во внешнем поле и включить ее
в механическую энергию системы. При
этом изменение механической энергии
системы
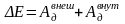 ,
где
,
где
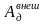 – работа внешних непотенциальных сил,
– работа внешних непотенциальных сил,
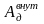 – работа внутренних непотенциальных
сил.
– работа внутренних непотенциальных
сил.
Момент импульса системы
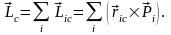
Изменение момента импульса системы
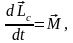
где
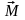 – сумма моментов внешних сил относительно
центра инерции.
– сумма моментов внешних сил относительно
центра инерции.
Момент
импульса изолированной системы частиц
сохраняется: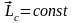 .
.
Законы сил
Закон всемирного тяготения:
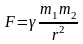 ,
,
где

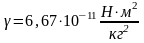 – гравитационная постоянная. Закон
справедлив для материальных точек и
шаров со сферическим распределением
массы, где r
– расстояние между точками или центрами
шаров.
– гравитационная постоянная. Закон
справедлив для материальных точек и
шаров со сферическим распределением
массы, где r
– расстояние между точками или центрами
шаров.
Сила тяжести:
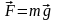 ,
,
где
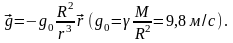
Сила упругих деформаций растяжения-сжатия (закон Гука):
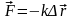 ,
,
где k
– коэффициент упругости,
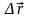 – перемещение конца тела.
– перемещение конца тела.
Максимальная сила трения покоя и сила трения скольжения
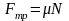 ,
,
где m – коэффициент трения, N – сила реакции поверхности.
Сила сопротивления (u<uзв):
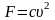 ,
,
где с – коэффициент сопротивления, зависящий от плотности среды, формы и размеров тела.
Сила вязкого трения:
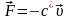 ,
,
где
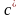 зависит от вязкости среды, формы и
размеров тела. Например, для шара (закон
Стокса):
зависит от вязкости среды, формы и
размеров тела. Например, для шара (закон
Стокса):
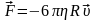 ,
где R
– радиус шара, h
– вязкость среды.
,
где R
– радиус шара, h
– вязкость среды.
Динамика вращательного движения тел вокруг
неподвижной оси
Момент инерции тела относительно оси вращения
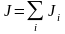 ,
,
где
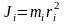 – момент инерции материальной точки
относительно оси вращения (mi
– масса материальной точки, ri
-расстояние от точки до оси вращения).
– момент инерции материальной точки
относительно оси вращения (mi
– масса материальной точки, ri
-расстояние от точки до оси вращения).
Момент импульса тела относительно оси вращения
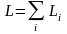 ,
,
где
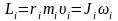 – момент импульса материальной точки
относительно оси вращения.
– момент импульса материальной точки
относительно оси вращения.
Момент силы относительно оси вращения
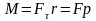 ,
,
где
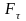 – касательная составляющая силы, r
– расстояние от точки приложения силы
до оси вращения, р
– плечо силы.
– касательная составляющая силы, r
– расстояние от точки приложения силы
до оси вращения, р
– плечо силы.
Основной закон динамики вращательного движения тела относительно неподвижной оси в дифференциальной форме:
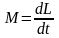 ,
,
где
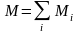 – сумма моментов внешних сил.
– сумма моментов внешних сил.
Основной закон динамики вращательного движения тела относительно неподвижной оси в интегральной форме:
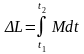 .
.
Момент импульса замкнутой системы тел, вращающихся вокруг общей оси, сохраняется:
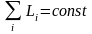 .
.
Работа момента силы
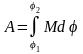 .
.
Кинетическая энергия вращения
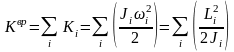 .
.
Теорема о кинетической энергии:
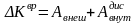 ,
,
где
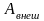 – работа внешних сил,
– работа внешних сил,
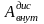 – работа внутренних диссипативных сил.
– работа внутренних диссипативных сил.
Динамика вращательного движения твердого тела относительно неподвижной оси
Момент импульса твердого тела относительно оси вращения
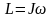 ,
,
где
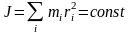 – момент инерции твердого тела
относительно оси вращения, w
– угловая скорость вращения твердого
тела.
– момент инерции твердого тела
относительно оси вращения, w
– угловая скорость вращения твердого
тела.
Основной закон динамики вращательного движения твердого тела относительно оси вращения:
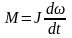 ,
,
где – сумма моментов внешних сил относительно оси вращения.
Теорема Штейнера:
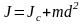 ,
,
где Jc – момент инерции твердого тела относительно оси, проходящей через центр инерции и параллельной данной оси, m – масса тела, d – расстояние между осями.
Момент инерции сплошного цилиндра радиусом R относительно оси цилиндра
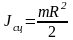 .
.
Момент инерции тонкого стержня длиной l относительно оси, проходящей через его центр и перпендикулярной к стержню,
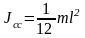 .
.
Момент инерции шара радиусом R относительно оси, проходящей через центр шара,
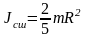 .
.
Плоское движение твердого тела
Основные уравнения плоского движения твердого тела:
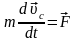 ,
,
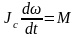 ,
,
где m – масса тела, – скорость центра масс, – сумма внешних сил, Jc – момент инерции тела относительно оси, проходящей через центр инерции, М – сумма моментов внешних сил относительно оси, проходящей через центр инерции.
Кинетическая энергия плоского движения твердого тела
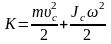 .
.
Механические колебания
Уравнение гармонических колебаний:
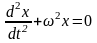 ,
,
где
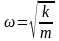 – циклическая частота (k
– коэффициент квазиупругой силы, m
– масса тела).
– циклическая частота (k
– коэффициент квазиупругой силы, m
– масса тела).
Связь циклической частоты с периодом колебаний
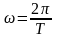 .
.
Период колебаний тела, подвешенного на пружине,
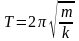 ,
,
где k – жесткость пружины.
Период колебаний математического маятника
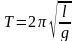 ,
,
где l – длина маятника, g- ускорение силы тяжести.
Период колебаний физического маятника
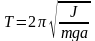 ,
,
где J – момент инерции колеблющегося тела относительно оси колебаний, a – расстояние от оси колебаний до центра тяжести.
Уравнение движения гармонических колебаний
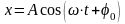 ,
,
где A – амплитуда, j0 – начальная фаза.
Скорость гармонических колебаний
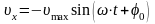 ,
,
где
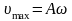 – амплитудное значение скорости.
– амплитудное значение скорости.
Ускорение гармонических колебаний
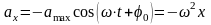 ,
,
где
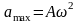 – амплитудное значение ускорения.
– амплитудное значение ускорения.
Уравнение затухающих колебаний
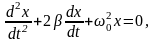
где
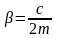 коэффициент затухания,
коэффициент затухания,
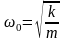 – циклическая частота собственных
колебаний (с
– коэффициент пропорциональности в
законе вязкого трения
– циклическая частота собственных
колебаний (с
– коэффициент пропорциональности в
законе вязкого трения
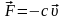 ,
m
– масса тела).
,
m
– масса тела).
Уравнение движения затухающих колебаний (w0>b):
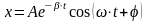 ,
,
где
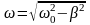 – циклическая частота затухающих
колебаний.
– циклическая частота затухающих
колебаний.
Декремент затухания
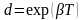 ,
,
где
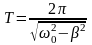 – период затухающих колебаний.
– период затухающих колебаний.
Логарифмический декремент затухания
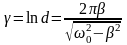 .
.
Уравнение вынужденных колебаний:
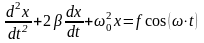 ,
,
где
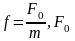 – амплитудное значение вынуждающей
силы, w
– циклическая частота вынуждающей
силы.
– амплитудное значение вынуждающей
силы, w
– циклическая частота вынуждающей
силы.
Уравнение движения вынужденных колебаний в установившемся режиме:
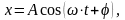
где
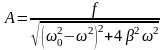 ,
,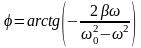 .
.
Резонансная частота
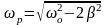 .
.
Резонансная амплитуда
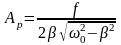 .
.
