1. Кинематика Основные понятия, соотношения, формулы

Перемещение

где - радиус-векторы начального и конечного положения точки.

Средняя скорость точки

Мгновенная скорость точки

Средняя путевая скорость

где DS – путь, пройденный точкой за время Dt.

Скалярная скорость

Среднее ускорение точки

Мгновенное ускорение точки

Ускорение точки в проекциях на касательную и нормаль к траектории

Модуль полного ускорения

Равномерное прямолинейное движение

Скорость

Перемещение

Уравнение движения

Равнопеременное движение

Ускорение

Скорость

Уравнение движения

Средняя скорость

Перемещение

Кинематическое соотношение

Движение точки по окружности и вращение твердого тела

Угловое перемещение

где j_1,j2– полярные углы начального и конечного положения точки (тела).

Средняя угловая скорость

Мгновенная угловая скорость

Среднее угловое ускорение

Мгновенное угловое ускорение

Равномерное вращение

Угловая скорость w=const.

Уравнение движения j=j₀+wt.

Угловое перемещение Dj=wt.

Число оборотов

Период вращения

где – частота вращения.

Равнопеременное вращение

Угловое ускорение e=const.

Угловая скорость w=w₀+et.

Уравнение движения

Средняя угловая скорость

Угловое перемещение

Кинематическое соотношение w²-w₀²=2eDj.

Связь между линейными и угловыми

кинематическими величинами

DS=RDj,

где DS- путь, Dj- угловое перемещение, R– радиус окружности.

u=wR,

гдe u– скалярная скорость, w-угловая скорость, R- радиус окружности.

at=eR,

где at - величина касательного ускорения, e-угловое ускорение.

a_n=w²R,

где a_n- величина нормального ускорения.

,

где a- величина полного ускорения.

Преобразование Галилея

Преобразование координат:

Преобразование времени:

Закон сложения скоростей:

Примеры решения задач

Задача 1. Человек плывет относительно воды со скоростью, в N раз меньшей скорости течения реки. Под каким углом _m (град) к направлению течения пловец должен держать курс, чтобы его снесло течением реки как можно меньше? Определите величину сноса S_min(м), если ширина реки h (м).

Решение. В выбранной системе координат уравнение движения пловца имеет вид

, где

( – скорость течения воды в реке,

– скорость пловца относительно воды).

П редставим уравнение движения пловца в проекциях на координатные оси:

,

Исключая время из последних соотношений, найдем уравнение траектории

,

г де . Траектория пловца – прямая линия.

Положив в уравнении траектории x=S, y=h, найдем зависимость сноса пловца от угла 

.

Эта функция минимальна при угле _m (убедитесь в этом). Находим a_m из условия экстремума ( ):

Минимальный снос пловца равен

.

Вычислите с необходимой точностью a_m (град) и S_m (м) для значений =1,7 и h=53 м.

Задача 2. Из поселка К, находящегося на автомагистрали, необходимо за кратчайшее время попасть в деревню L, расположенную в поле на расстоянии S (км) от поселка и видимую под углом a (град) к направлению магистрали. Предельная разрешенная скорость движения автотранспорта по магистрали u_a (км/ч), она превышает скорость движения по полю в N раз. В каком месте магистрали следует свернуть в поле? Чему равно минимальное время движения?

Р ешение. Введем обозначения: x, L=S. Выразим общее время движения как функцию расстояния x:

Представим это соотношение в безразмерных величинах :

.

Функия имеет минимум (убедитесь в этом). Расстояние , соответствующее минимальному времени движения, найдем из условия экстремума :

Расстояние для . Минимальное время движения равно

.

Вычислите с необходимой точностью x_m (км) и t_min (мин) для значений S=12 км, u_a=72 км/ч, N=2,8, =52°.

Задача 3. Первую половину пути точка движется равномерно со скоростьюu₁, вторую – со скоростью u₂ (u_1¹u2). Чему равна средняя путевая скорость точки .

Решение. Обычно следует ответ по аналогии с равнопеременным движением. Но это неверно. Рассматриваемое движение не относится к разряду равнопеременных (a=const), для которых средняя скорость для интервала времени от t₁ до t₂ равна полусумме скоростей в начале и в конце интервала времени.

В этом можно убедиться, анализируя график скорости. Из рисунка видно, что

, так как заштрихованные площади равны.

Найдем точное решение. Воспользуемся для этого определением средней путевой скорости:

Из решения видно, что , так как , если (u_1¹u2).

Задача 4. Две точки движутся с переменными ускорениями, изменяющимися с течением времени согласно кривым 1 и 2. Сравните средние ускорения точек для интервала времени t=[0, t₁].

Решение. Ответ: <a_x>₁ < <a_x>₂.

Обоснование связано с определением средней величины и ее геометрической интерпретацией. Среднее ускорение определяется отношением приращения скорости к интервалу времени, за которое произошло это приращение:

где , t =t₁.

В соответствии с геометрической интерпретацией интеграла приращение Du_x равно площади под кривой a_x (t).Так как Du_x2>Du_x1, t₁=t₂=t₁, то <a_x>₁<<a_x>₂.

Задача 5. Частицы начинают двигаться в однородном поле тяжести Земли с начальными скоростями и .

С равните: а) время движения частиц, б) дальность полета частиц, в) радиус кривизны траектории в наивысшей точке подъема. Сопротивлением воздуха пренебречь.

Решение. Правильные ответы: а) t₁<t₂, б) S₁<S₂ в)R₁=R₂.

Произвольное движение, в частности плоское движение, всегда можно представить как сумму независимых движений вдоль выбираемых координатных осей (принцип независимости движений). Этот принцип позволяет при качественном анализе представить сложное механическое движение как совокупность простых, хорошо изученных движений, например равномерного, равнопеременного и гармонического колебания.

В данной задаче плоское движение в однородном поле тяжести Земли представлено суммой двух независимых движений: равномерного движения вдоль оси Ох и равнопеременного движения с ускорением свободного падения по оси Оу. Из рисунка видно, что проекции начальных скоростей на горизонтальное направление у частиц одинаковы. Это обстоятельство является ключевым для сравнительной оценки движений. Общее время движения частицы складывается из времени подъема и времени падения частицы, которые, как известно, равны между собой. Так как у второй частицы вертикальная составляющая начальной скорости больше, чем у первой, она поднимется на большую высоту и затратит большее время на подъем. Таким образом, общее время движения второй частицы будет больше, чем первой (t₂>t₁). Горизонтальное смещение второй будет также больше, чем первой, так как горизонтальные составляющие скорости у частиц одинаковы, но вторая частица находится в движении дольше.

В верхней точке траектории вертикальная составляющая скорости равна нулю, и скорость частицы становится равной горизонтальной составляющей u_x. Нормальное ускорение в этой точке равно

,

где R – радиус кривизны траектории.

Так как в верхней точке тангенциальное ускорение равно нулю, то нормальное ускорение равно ускорению свободного падения g. Следовательно, радиусы кривизны траектории в верхней точке равны: R₁=R₂.

Задача 6. Зенитное орудие может сообщить снаряду начальную скорость u₀=500 м/с в любом направлении. Требуется найти границу, отделяющую цели, до которых снаряд из данного орудия может долететь, от недостижимых целей. Сопротивлением воздуха пренебречь.

С

Решение

u₀=500 м/с

g=10 м/с²

у (х) - ?

начала попробуем выяснить, что можно сказать об этой границе. Сам факт ее существования не вызывает сомнений. Очевидно, она представляет собой некоторую поверхность, которая обладает свойством осевой симметрии. Поэтому эту поверхность можно представить как поверхность вращения некоторой кривой вокруг вертикали, проходящей через орудие. Таким образом, проблема сводится к нахождению уравнения этой плоской кривой у (х). Вначале выясним параметры этой кривой. Если цель находится над орудием, то стрелять нужно вертикально вверх. Снаряд при этом поднимается на максимальную высоту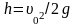 , после чего падает вниз. Кривая пересекает вертикаль в точке, находящейся на высоте h. Если ограничиться целями, находящимися на поверхности Земли, то граница представляет собой окружность, радиус которой равен максимальной дальности полета снаряда по горизонтали 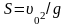_. Максимальная дальность полета достигается при угле возвышения a=45° (убедитесь в этом). Кривая пересекает ось Ох в точках х=±S.

Приступим к решению задачи. Запишем уравнение движения снаряда:

,

или в проекциях на оси координат

.

Исключая из последних уравнений время t, получим уравнение траектории снаряда

.

Это уравнение описывает семейство кривых (парабол), зависящих от угла возвышения  при фиксированном значении начальной скорости снаряда u₀=const. Но этому же уравнению можно придать и другой смысл. Будем считать, что х и у – это координаты цели, в которую попадает снаряд, двигаясь по некоторой траектории. Тогда при заданных координатах цели х и у уравнение траектории снаряда определяет угол , под которым нужно выпустить снаряд с начальной скоростью u₀ для того, чтобы он попал в эту цель. Чтобы получить координаты максимально удаленной цели, нужно исследовать зависимость у(х, tg) на экстремум относительно параметра tg. Взяв производную по этому параметру, приравняв ее к нулю, получаем

.

Подставив последнее условие в уравнение траектории снаряда, находим для граничной кривой следующее уравнение:

.

Это уравнение параболы с вершиной при x=0, называется параболой безопасности. Коэффициент при х² отрицателен, т.е. ветви направлены вниз и пересекают горизонтальную ось в точках . Итак, полученная граница действительно проходит через точки, которые были установлены из элементарных соображений.

Отметим, что этот же результат можно получить средствами элементарной математики. Для этого надо уравнение траектории снаряда выразить относительно параметра tg. Положив дискриминант квадратного уравнения равным нулю, получаем уравнение для границы.

Для принятых в условии задачи данных “парабола безопасности” описывается уравнением

y=1,25·10⁴-2,0·10^-5x².

З

Решение

S=400 м

h=40 м

g=10 м/с²

_m- ? u_min- ?

адача 7. Судно стоит на расстоянии S=400 м от отвесного берега моря. Высота берега h=40 м. С берега на судно бросают груз. Под каким углом _m следует бросить груз, чтобы его скорость при падении на судно была минимальной? Чему равна эта скорость? Сопротивлением воздуха пренебречь.

Г руз движется по параболе:

(см. задачу 6), конец которой должен совпадать с координатами судна у=0, х=S. Подставив координаты судна в уравнение траектории, получаем уравнение, связывающее начальную скорость u₀ с углом 

.

Очевидно, что скорость груза при падении на судно будет минимальной, если минимальна начальная скорость u₀.

Функция (tg) имеет минимум (убедитесь в этом) при

.

Минимальная начальная скорость равна

.

Для минимальной скорости груза при падении на судно получаем

Найдите значения _m и u_min для численных данных задачи. Исследуйте зависимость _m и u_min от высоты h и сделайте соответствующие выводы.

З адача 8. Цель находится на склоне горы на высоте h=50 м. Высота горы H=150 м. Расстояние от миномета до вершины горы равно a=500 м, а до цели (a + в)=800 м. Определите величину минимальной начальной скорости мины u_{o min} . Под каким углом a_m к горизонту при этом следует вести стрельбу? Сопротивлением воздуха пренебречь.

Решение

h =50 м

H=150 м

а=500

a+b=800

g=10 м

u _{o min} - ?

a _m - ?

Исследуем уравнение траектории мины (см. задачу 6):

.

Выделим траектории, которые проходят через цель с координатами x=(a+b), y=h:

.

При этом начальная скорость мины должна удовлетворять условию

.

Среди этих траекторий для нас интерес представляют те, которые огибают гору. Допустим, что условие у(а )>Н выполнено. Исследуем зависимость u₀²(tga). Эта функция имеет минимум при

.

Решение со знаком “-” не удовлетворяет условию .

Минимальная начальная скорость при этом равна

.

В частном случае (h=0) (цель находится у подножья горы)

.

Если у(а)<H при угле a_m, то необходимо выбрать траекторию, которая касается вершины горы. Из условия y(a)=H находим для угла a соотношение

.

Соответствующая этому углу a начальная скорость мины равна

.

В частном случае (h=0)

.

Рассмотрим, к какому случаю относятся наши данные. Вычислим tga_m=1,064, a_m=46,8⁰. Тогда у(а)=180 м. Таким образом, так как у(а)>H=150 м, стрельба должна вестись под углом a_m»47⁰ при минимальной скорости мины u_{0 min}=92 м/с.

Задача 9. Точка движется с постоянной по величине скоростью (u=const) по плоской криволинейной траектории (см. рисунок). Сравните ускорение точки в положениях А и В.

Решение. Правильный ответ: а_А>а_В.

Э та качественная задача связана с выяснением знания определений таких кинематических величин, как касательное, нормальное и полное ускорения. По определению касательное ускорение характеризует изменение величины скорости

.

В нашем случае величина скорости не изменяется, поэтому аt=0.

Величина нормального ускорения в каждой точке траектории связана с радиусом кривизны соотношением:

Модуль полного ускорения равен

Таким образом, а_А > a_B , так как u=const, R_A < R_B.

З адача 10. При движении точки по окружности угловая скорость изменяется с течением времени согласно соотношению w~tⁿ>, где n>0. При этом тангенс угла между вектором ускорения и вектором скорости изменяется с течением времени как t^m. Определите значение m.

Решение

w~tⁿ

tga~t^m

m-?

Для плоского движения ускорение можно представить как сумму касательного и нормального ускорений:

.

Откуда (см. рисунок).

Учитывая, что

,

,

так как R=const, находим

Таким образом, m=n+1.

Задача 11. Твердое тело вращается вокруг неподвижной оси так, что его угловая скорость зависит от угла поворот j согласно уравнению w=w₀-aj , где w₀=12 рад/с , a=0,15 1/с. Определите предельные значения угла поворота и угловой скорости, если в начальный момент времени j(0)=0.

Н

Решение

w₀=12 рад/с

а=0,15 1/с

j(0)=0

j_пр-?, w_пр -?

айдем уравнение вращательного движения твердого тела j(t).Угловая скорость по определению равна:

.

Интегрируя последнее уравнение с учетом j(0)=0, получаем

.

Подставив j(t) в выражение для угловой скорости, находим

.

В пределе при t®¥

, w_пр=0.

Задача 12. Самолет, летящий горизонтально со скоростью u₀, начинает подниматься вверх, описывая окружность, лежащую в вертикальной плоскости. Скорость самолета при этом меняется с высотой h над первоначальным уровнем движения согласно соотношению u²=u₀²-na₀h, где а₀=10 м/с², n=3. В верхней точке траектории его скорость оказывается равной . Определите ускорение а самолета в тот момент , когда его скорость составляет угол j=90⁰ с горизонтом.

Р ешение. Величина полного ускорения самолета равна

,

где .

Выразим высоту самолета через угол j и радиус окружности R (см. рисунок):

.

Закон изменения скорости будет иметь вид

.

По условию при j=p. Тогда квадрат начальной скорости равен

.

Для нормального и касательного ускорений в произвольной точке окружности получаем

,

.

Полное ускорение равно

40 м/с².