2.8. Методы прогнозирования в уз:

Для прогнозирования потребности в продукции при определении размера заказа в системах управления запасами применимы различные методы прогнозирования.

Одним из наиболее распространенных методов прогнозирования является метод экстраполяции тренда.

Метод экстраполяции тренда:

В основе метода экстраполяции тренда лежит предположение о том, что закономерность, действующая внутри анализируемого временного ряда, выступающего в качестве базы прогнозирования, является достаточно устойчивой и сохраняется на период прогноза. Прогнозирование в этом случае можно свести к подбору аналитически выраженных моделей типа y=f(t) с учетом трендов.

Модели трендов могут быть аддитивными и мультипликативными.

Аддитивная модель тренда:

, (15)

где y_t – прогнозные значения временного ряда;

- среднее значение прогноза (тренд);

s_t – составляющая прогноза, отражающая периодические колебания, которые повторяются через примерно одинаковые промежутки в течение небольшого промежутка времени (сезонные колебания или сезонная волна);

v_t – составляющая прогноза, отражающая периодические колебания, повторяющиеся в течение длительного промежутка времени (циклические колебания);

d_t – составляющая, позволяющая учесть другие важные для конкретного прогноза;

- случайная величина отклонения прогноза.

Мультипликативная модель тренда:

, (16)

где y_t – прогнозные значения временного ряда;

- среднее значение прогноза (тренд);

I_s – коэффициент (индекс), учитывающий сезонные колебания;

I_v – коэффициент (индекс), учитывающий циклические колебания;

I_d – коэффициент (индекс), учитывающий другие важные для конкретного прогноза факторы (фаза жизненного цикла, эффект от маркетинговых мероприятий и др.);

- случайная величина отклонения прогноза.

Тренд, сезонная, случайная и др. составляющие в аддитивной модели (тренд и случайная составляющая в мультипликативной модели) представляют собой функциональные зависимости (линейную, степенную, экспоненциальную, логарифмическую, синусоидную, косинусоидную и проч.), параметры которых могут быть найдены методом наименьших квадратов.

План прогноза с использованием метода экстраполяции тренда выглядит следующим образом:

1. задаются видом тренда временного рада;

2. с использованием метода наименьших квадратов определяют коэффициенты уравнения тренда;

3. исследуют сезонные колебания и определяют (при наличии сезонной волны) коэф­фициенты уравнения, выбранного для аппроксимации;

4. определяют случайные величины отклонений;

5. оценивают ошибку прогноза;

6. определяют доверительный интервал прогноза.

Погрешность прогноза отражается в виде доверительного интервала:

(17)

где ∆y– доверительный интервал прогноза;

- прогнозное значение;

t_α – табличное значение t-критерия Стьюдента с k степенями свободы и уровнем значимости p;

S_y – погрешность прогноза.

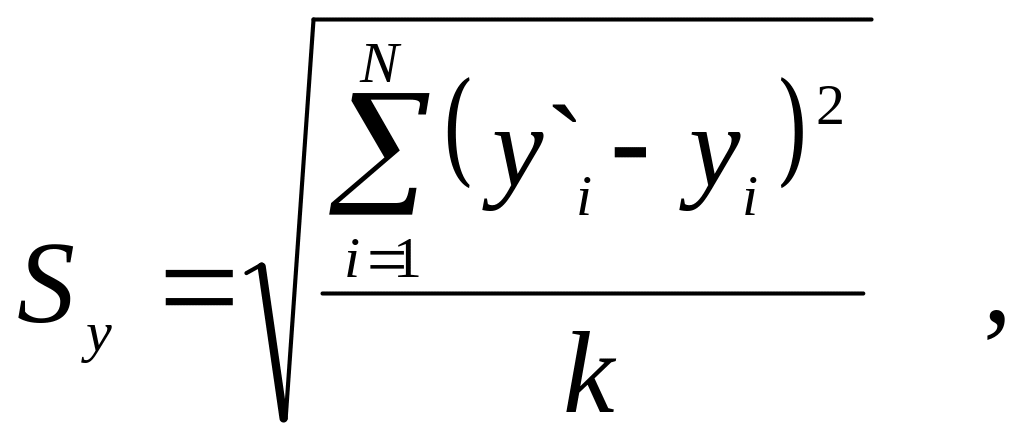(18)

где S_y – погрешность прогноза.

y_i `– расчетное (теоретическое) значение;

y_i – фактическое значение;

k – число степеней свободы, определяемое в зависимости от числа наблюдений и числа оцениваемых параметров;

Наибольшее распро­странение среди методов прогнозирования получили методы сглаживания. Данные модели могут использоваться в непрерывных самоулучшающихся прогнозных системах, что представляет практический интерес особенно в сфере определения потребности в запасных частях.

Метод экспоненциального (простого) сглаживания. Прогнозируемое значение y^*_t+1 в момент времени t+1 представляет собой сумму фактического значения показателя y_t и прогнозируемого значения y_t^* в момент времени t [20]:

, (19)

где α – параметр сглаживания, определяющий значение веса, которое имеет самое последнее наблюдение при вычислении прогноза на один шаг; .

Процедура побора параметра α сводится к поиску такого значения , которое обеспечивает наименьшую погрешность – среднеквадратичное отклонение:

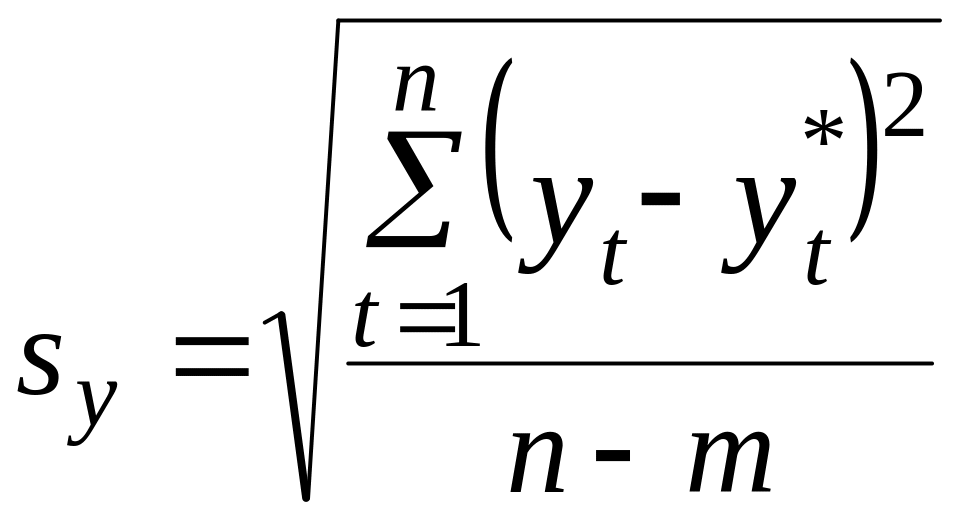, (20)

где n – число учитываемых периодов времени (можно принять как число данных исходного ряда); m – количество параметров показательного сглаживания (модель (1.1) однопараметрическая, поэтому m=1).

Модель экспоненциального сглаживания по Хольту включает 3 этапа:

1. сглаживание данных:

; (21)

2. сглаживание тренда:

; (22)

3. прогноз на период t+k:

, (23)

где а_t – сглаженное значение прогнозируемого показателя для периода t;

b_t – оценка прироста тренда, показывающая возможное возрастание или убывание значений за один период;

α, β – параметры сглаживания ( ; );

k – количество периодов времени, на которые производится прогноз.

Экспоненциальное сглаживание с тремя параметрами, отражающими тренд и сезонность изменений (модель Винтерса) включает четыре уравнения:

1. сглаживание исходного ряда:

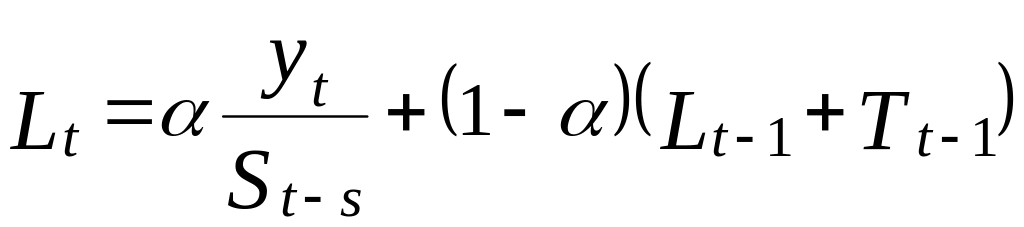; (24)

2. сглаживание тренда

; (25)

2. оценка сезонности

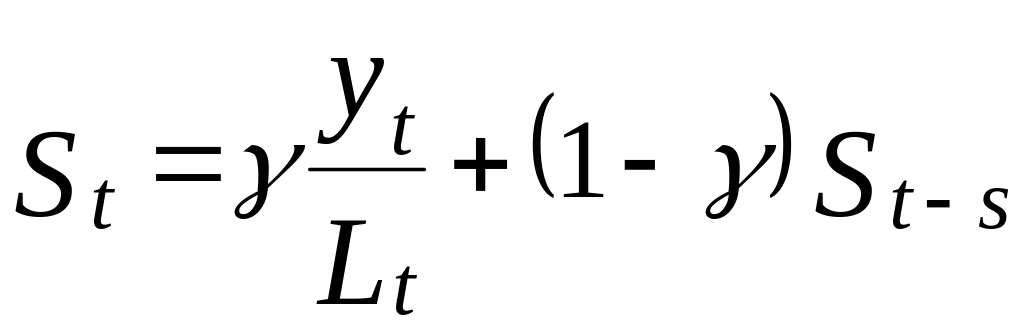; (26)

2. прогноз на р периодов вперед

, (27)

где L_t – сглаженное значение ряда;  – параметр сглаживания данных; y_t – фактическое значение показателя для периода t;  – параметр сглаживания для оценки тренда; T_t – оценка тренда;  – параметр сглаживания для оценки сезонности; S_t – оценка сезонности; p – количество периодов, на которое строится прогноз; s – длительность периода сезонных колебаний.

Параметры сглаживания должны соответствовать условиям:

; ; (28)

Прежде чем применять уравнения (58)-(61) необходимо задать начальные условия. Существует два варианта выбора начальных условий в модели Винтерса. Первый предполагает, что начальное значение сглаженного ряда (L_s) равно первому наблюдению. Тогда тренд (T_s) равен нулю, а коэффициенты сезонности (S_t-s) устанавливаются равными 1. Второй вариант назначения начальных условий предполагает, что начальное значение для сглаженного ряда (L_t-1) равно среднему значению за первые s наблюдений. Тогда начальные условия для тренда (T_t-1) определяются наклоном прямой, образованной этими наблюдениями. Коэффициенты сезонности равны:

, (29)

где L_s – начальное условие для сглаживания данных.

Параметры сглаживания могут быть определены путем минимизации ошибки прогнозирования с помощью процедуры «Поиск решения» MS Exсel.

Комбинированная оценка прогноза производится только для непротиворечивых прогнозов. Поэтому прежде чем приступить к комбинированному прогнозу, необходимо произвести логический анализ прогнозов, полученных различными методами, и оценить их непротиворечивость. Для этого сначала следует произвести статистическую обработку экспертных оценок – найти среднее значение и среднее квадратическое отклонение для экспертного прогноза. Каждому значению прогноза присваивается новый номер таким образом, что разряду с наименьшей суммой баллов присваивается номер 1 и т.д. Вероятности гипотез определяются по формуле:

(31)

где i – ранг, соответствующий значению Y_i, которые предлагались экспертам при опросе; n - обще количество рангов.

Для «экспертной» плотности распределения находятся среднее значение (значение экспертного прогноза):

(32)

и дисперсия (корень из дисперсии – ошибка прогноза):

(33)

Затем прогнозы проверяются на непротиворечивость. Если прогнозы согласованы, то определяются весовые коэффициенты прогнозов по формуле:

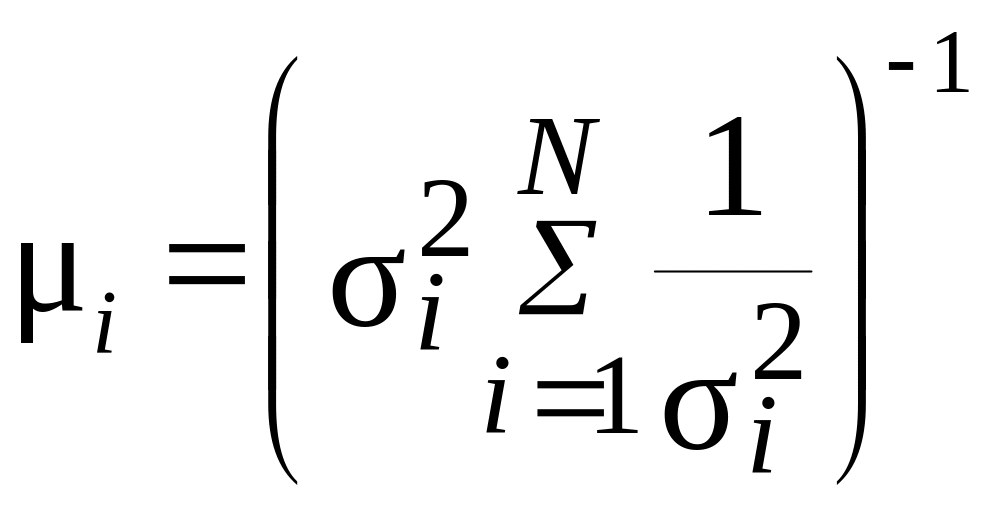, (34)

где N – количество прогнозов, участвующих в комбинированной оценке.

Далее рассчитываются среднее значение комбинированного прогноза

, (35)

дисперсия комбинированного прогноза

, (36)

где _i² – дисперсия i-го прогноза,

и вероятности комбинированного прогноза.

Для определения вероятности комбинированного прогноза предварительно необходимо найти плотность распределения для прогноза, полученного, например, по трендовой модели. При этом принимается, что данные прогнозные оценки распределены нормально. Вероятность прогноза равна:

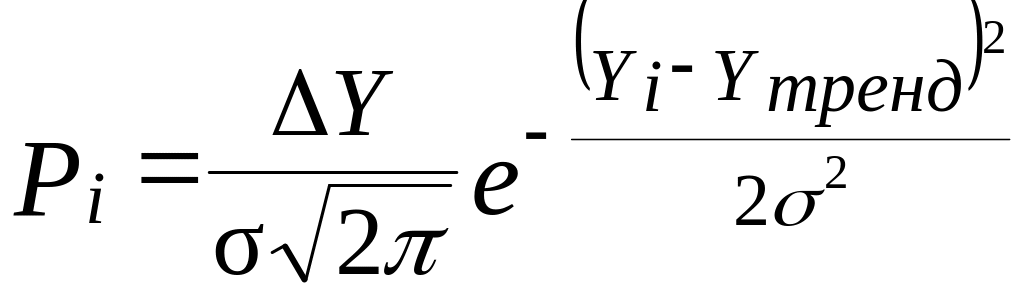. (37)

Пример 3:

В таблице 8 приведены фактические данные о квартальном потреблении газа за 5 лет. График изменения потребления газа показан на рис. 6. Требуется определить значение сезонной составляющей при условии, что тренд линейный. Спрогнозировать потребление газа на 1997 год.

Сумма случайной и сезонной составляющих будет рассчитываться по формуле:

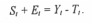
и т.д.

Таблица 8

Расчет сезонной составляющей в потреблении газа для прогнозирования оптимальных запасов газа в хранилищах
Год	Квартал	№	Потребление гада, м3 - Yt	Тренд - Tt	Сезонная составляющая + случайная составляющая	Квартал	Сезонная составляющая (по кварталам)
1992	1	1	9157539			1	2272468,938
	2	2	5841223			2	-1600262,969
	3	3	4535986	7042367	-2506381	3
	4	4	8634521	6979178,38	1655342,625	4
1993	1	5	9157937
	2	6	5335316
	3	7	4664046
	4	8	9123280
1994	1	9	9409531
	2	10	5637070
	3	11	4405104
	4	12	8594426
1995	1	13	9065812
	2	14	5395462
	3	15	4775631
	4	16	8774019
1996	1	17	9550668
	2	18	5285475
	3	19	4599996
	4	20	8252932
Комментарий			Фактические значения	Сглаживание данных	Находим отклонение факт данных от данных тренда	Среднее значение сезонной и случайной для соответствующего квартала
Прогноз на 1997 год
1997	1	21
	2	22
	3	23
	4	24

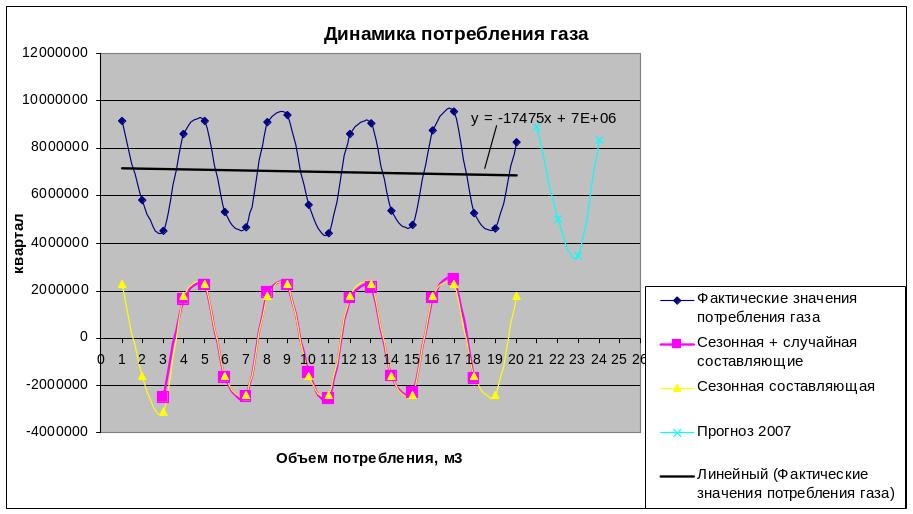
Рис. 6.