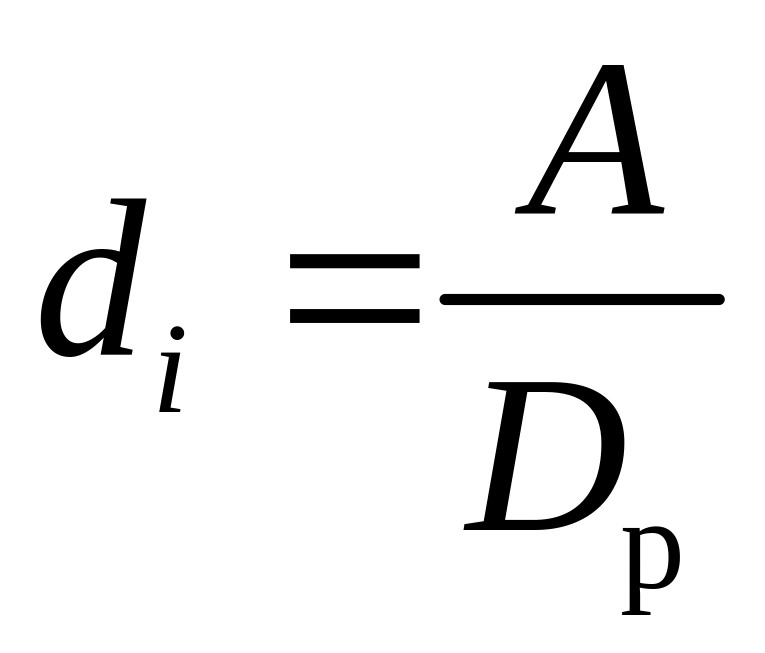3. Классификация стратегий управления запасами:

В литературе встречаются примеры различных классификаций стратегий управления запасами и их модификаций:

Классификация стратегий управления запасами

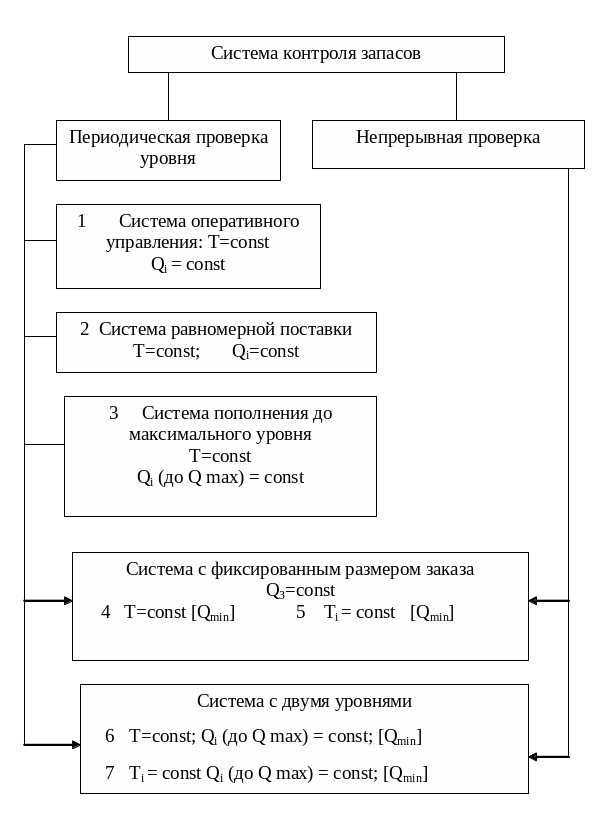
Рис. 2

Классификация В.И. Сергеева:

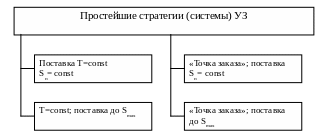
Рис.3.

Исследования, проведенные на кафедре Логистики и организации перевозок СПб ГИЭУ, показали, что могут быть выделены две основные (базовые) стратегии управления запасами, на основе которых выстраиваются остальные, модифицированные, стратегии:

1. Система (стратегия) с фиксированным интервалом времени между заказами (ФПЗ);

2. Система с фиксированным размером заказа (ФРЗ).

Различные стратегии управления запасами формируются на основе двух простейших моделей: периодической (фиксированный интервал между заказами) и критических уровней (фиксированный уровень (точка) заказа). В периодических моделях заказ производится в каждом периоде t_п через равные интервалы времени; в моделях с критическим уровнем S_з при уменьшении текущего запаса на складе S_т до величины S_з (точка заказа).

Второе отличие в простейших моделях состоит в выборе объема поставки:

первый вариант – объем поставки S_п постоянный;

второй вариант – объем поставки переменный S_i, восполняющий наличный запас до верхнего критического (максимального) уровня S_max .

Таким образом, сочетание двух моментов заказа и двух вариантов объемов заказа позволяет получить четыре простейшие стратегии управления запасами: (Т, S_п), (Т, S_max), (S_з, S_п), (S_з, S_max) – см. рис. 3.

2.4. Система (стратегия) с фиксированным интервалом времени между заказами (фпз) и ее модификации:

Система с фиксированным интервалом времени между заказами или с фиксированной периодичностью заказа (ФПЗ) – это система, в которой период между заказами является постоянной величиной (месяц, половина месяца и т.д.). В конце каждого периода (цикла) проверяется уровень запаса и с учетом остатка S_Ti и прогнозного значения расхода запаса за время поставки S_п(τ) рассчитывается размер заказываемой партии S_зi. Считается, что каждый раз при поставке S_зi запас в системе восполняется до максимального уровня S_max.

Считается, что данная система наиболее эффективна на универсальных складах, когда имеется возможность варьировать размер партии поставки, а транспортно-транзитные расходы относительно невелики.

Для формирования параметров ФПЗ необходимо знать следующие показатели:

1. Интервал времени между заказами – Т, дн.;

2. Потребность в заказываемом продукте А, ед. и среднесуточный расход (интенсивность) d_с, ед./дн. ;

3. Время выполнения заказа – τ.

Рассмотрим, как определяются указанные показатели:

Интервал времени между заказами Т может быть выбран различными способами: расчетным путем или эмпирическим, с учетом сложившейся практики проверки (инвентаризации) запасов на складе, например, 15 числа каждого месяца.

Если при разработке системы с ФПЗ используется модель EOQ, то расчетная величина Т определяется по формуле

(1)

где S_о – оптимальная партия поставки;

D_р- число рабочих дней за рассматриваемый период (например, 260 рабочих дней в году).

А – общая потребность в продукте за рассматриваемый период (например, годовая).

Если за основу принимаются статистические данные о предыдущих поставках, то величина Т рассчитываются по статистическим формулам (см. Тема 2, табл. 2.2, стр. 16-17 рабочей тетради).

Выбор периодичности Т связан с другим показателем - временем выполнения заказа τ. Если Т больше τ, то заказ производится между двумя смежными поставками. Это наиболее желательный вариант при формировании системы управления запасами с фиксированной периодичностью заказа. Если интервал заказа Т меньше времени выполнения заказа τ, то это приводит к появлению за время τ двух или более заказов. Другими словами, заказ производится в то время, когда предыдущий заказ не поступил потребителю. Это приводит к росту неопределенности системы управления запасами, особенно при больших вариациях ежедневного расхода и времени выполнения заказа.

При формировании системы управления запасами с ФПЗ возможны два варианта: детерминированный и стохастический (вероятностный).

При детерминированном подходе все показатели заданы в виде постоянных величин, а зависимости, например, расход текущего запаса, - в виде прямых линий.

Рассмотрим последовательность определения параметров системы с ФПЗ при детерминированном подходе:

Таблица 2

№	Показатель	Формула для расчета
1	Потребность за период (год, месяц) - А	Исходные данные (определяется на основе плана производства или реализации)
2	Интервал времени между поставками (и между заказами), дн. - Т	Sо – оптимальная партия поставки; Dр- число рабочих дней за рассматриваемый период (например, 260 рабочих дней в году). А – общая потребность в продукте за рассматриваемый период (например, годовая).
3	Время выполнения поставки, дн. - τ	Исходные данные (указываются обычно в договоре на поставку)
4	Возможное время задержки поставки, дн. – τ`	Исходные данные (эмпирически определяемое разумное наибольшее время, на которое может быть задержана поставка)
5	Ожидаемое дневное потребление (интенсивность потребления) , шт – di или λi.
6	Ожидаемое потребление за время поставки, шт. – Qпост
7	Максимальное потребление за время поставки, шт. – Qпост max
8	Страховой запас, шт. - Sстр
9	Максимально желательный объем запасов, шт. – Smax
10	Размер заказа, шт - Qзак	Sтек – текущий запас

При стохастическом подходе большинство показателей характеризуются средними значениями, средними квадратическими отклонениями и законами распределения.

Рассмотрим последовательность определения параметров системы с ФПЗ при вероятностном подходе.

1. Расчетными параметрами системы являются:

- страховой запас, ед.;

- максимальный запас, ед.;

- размер заказа, ед.

2. При заданной потребности А определяем среднесуточный расход

(2)

где D_р – расчетный период.

3. На основании обработки статистических данных уточняем показатель d_с (как среднее значение) и рассчитываем среднее квадратическое отклонение ежедневного расхода σ_d.

4. Определим (или зададимся) статистическими параметрами времени поставки: средним значением τ_с и средним квадратическим отклонением σ_τ.

5. Определим величину текущего запаса (расчетную)

(3)

6. Рассчитаем величину страхового (гарантийного) запаса S_с. Один из возможных вариантов расчета (при σ_τ=0)

(4)

где t_p – коэффициент, см. формулу (6.35).

При отсутствии статистических данных на основании экспертной оценки выбираем максимальный интервал запаздывания τ_max и рассчитываем величину страхового запаса

(5)

7. Рассчитаем величину максимального запаса как сумму текущего и страхового запасов:

(6)

Таким образом, рассчитанные параметры позволяют построить «сетку» из прямых линий, рис.4: объем заказа (S_max, S_c) – время (Т, τ), на которую наносятся точки и линии, характеризующие процесс поступления и расхода продукции.

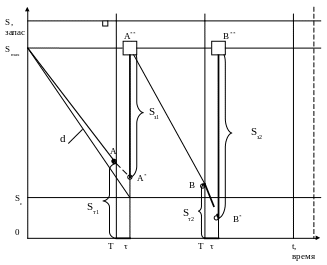
Рис.4. Система управления запасами с фиксированным интервалом времени между заказами

- остаток запаса в момент заказа (А)

- прогнозируемый остаток в момент поступления заказа (А^*)

- текущий запас в начале следующего интервала (А^**)

8. Спрогнозируем размер заказа S_з в момент времени Т

(7)

где S_тi – величина остатка текущего запаса на складе в момент Т_i;

S_п(τ) – прогнозное значение расхода запаса за время поставки τ.

Для расчета S_п(τ) можно воспользоваться двумя способами:

при небольшой вариации интенсивности ежедневного расхода продукции

(8)

при значительной вариации

(9)

где d_i – прогнозное значение интенсивности ежедневного расхода для i-й реализации.

При отсутствии какой-либо дополнительной информации о поступлении и расходе запаса для расчета d_i можно воспользоваться формулой

(10)

Пример 1:

Рассчитаем основные параметры системы управления запасами с ФПЗ на основе следующих исходных данных: А=2000 ед.; S_о=200 ед.; τ_с=5 дней; D_р=250 дней.

1. Рассчитаем интервал Т по формуле (1):

дней.

Следовательно, Можно допустить, что заказ производится один раз в месяц.

2. Определяем показатели среднесуточного расхода, формула (2):

ед./день

При отсутствии статистических данных принимаем, что ежедневный расход подчиняется нормальному закону распределения со средним квадратическим отклонением σ_d=3 ед./день.

3. Поскольку величина текущего запаса известна S_т=S_o=200 ед., то определим страховой запас по формуле (4) при t_p=2,0 (вероятность отсутствия дефицита Р=0,98):

ед.

Тогда, максимальный запас равен:

ед.

4. Выполним расчеты заказываемых партий для двух вариантов (см. рис.4): для точки А, соответствующей остатку текущего запаса S_т1=100 ед., и для точки В, соответствующей остатку текущего запаса S_т2=50 ед.

Для точки А воспользуемся формулой (10):

ед.

Прогноз расхода запаса за время поставки:

ед.

Размер заказа (прогнозное значение):

ед.

Прогноз остатка запаса в момент поставки (точка А^*):

ед.

При совпадении прогнозных значений в точках А и А^* уровень запаса составит S_max= 230 ед.

Аналогичны расчеты для точки В:

ед.; ед.; ед.; ед.; S_max= 230 ед.

В системе с фиксированной периодичностью заказа уровень запасов контролируется только в моменты осуществления заказа, поэтому при большой вариации среднесуточного расхода дефицит запасов может возникнуть как в период осуществления поставки, если этот период соизмерим с периодичностью заказа, так и в период времени между поставкой и временем заказа. Для устранения дефицита следует в первую очередь увеличить страховой запас и стремиться к более точному выполнению поставки.