
1 Встановлення кореляційного зв`яку для малої і великої кількості спостережень
Кореляційний зв`язок- це такий зв`язок між випадковими величинами коли одному відповідає деякий знак функції.
Для кількісних і якісних ознак які також використовують для характеристики більш поширених властивостей кореляційного зв’язку,
Характеристика зв’язків
-за формою:прямокутний або прямолінійний
-за напрямком:прямий(додатній)зворотний(відємний)
- за тіснотою: слабкий помірний значно тісний дуже тісний
Графічний спосіб-використовують для попереднього і наступного аналізу зв’язку між ознаками,
Форма напрямку зв’язку може бути виявлених тільки після проведеного кореляційного аналізу за отриманими показникаму зв’язку ,
Попередння наявність або відсутність зв’язку можна встановити двома способами графічним і табличним для цього результати спостережень наносять по координатним точкам і дивимся напрям і тісноту нанесення точок чим ближче розміщуються точки тим тісніший зв'язок між ними,
Питання № 2 Показники кореляційного звязку
Кореляційний звязок - це такий звязок між випадковими величинам, коли одному значеннюаргументу відповідає декілька значень функції.
Кореляційний звязок між випадковими величинами описують за формою, напрямом і тіснотою.
Форма звязку-може бути прямолінійною або криволінійною. Прямолінійною наз. така кореляція, коли однаковим змінам однієї величини відповідаютьоднакові зміни іншої.
Напрям звязку-прямий або зворотній.Залежність вважається прямою, якщо при збільшенні однієї ознаки інша також систематично зростає.
За ступенем тісноти може бути слабкою, помірною, значною, високою і дуже високою.
3.Кореляційний зв'язок- це такий звязокміж випадковими величинами , коли одному значенню аргументу відповідає декілька значень функції. Кореляційна залежність між Х та У називається лінійною кореляцією, якщо обидві функції регресії є лінійними. В такому випадку обидві лінії регресії є прямими; їх називають прямими регресії. Рівняння прямих регресії Х на У та У на Х мають вигляд:
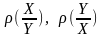
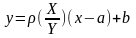
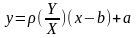
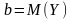
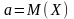
де
- кутові
коефіцієнти прямих регресії.
Кутовий коефіцієнт прямої регресії Х на У:
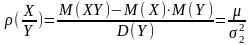
К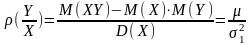 утовий
коефіцієнт прямої регресії У на Х:
утовий
коефіцієнт прямої регресії У на Х:
Значення кутових коефіцієнтів свідчить про силу кореляційного зв'язку: чим більший коефіцієнт ,тим сильнішим є кореляційний зв’язок. Сила зв'язку є важливою, але не достатньою характеристикою кореляційних залежностей.
Щ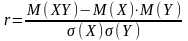 об
оцінити наскільки тісним є кореляційний
зв’язок між випадковими величинами
використовують коефіцієнт
кореляції r
,
який визначається за формулою:
об
оцінити наскільки тісним є кореляційний
зв’язок між випадковими величинами
використовують коефіцієнт
кореляції r
,
який визначається за формулою:
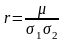
або більш простіше
д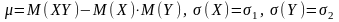 е
е
Я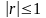 кщо
випадкові величини не залежать одна
від одної то r=0
.
Коефіцієнт кореляції може набувати
значення
кщо
випадкові величини не залежать одна
від одної то r=0
.
Коефіцієнт кореляції може набувати
значення
п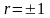 ричому
ричому
у випадках лінійної функціональної залежності між Х та У.
В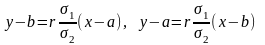 икориставши
коефіцієнт кореляції рівняння регресії
можна записати в наступному вигляді:
икориставши
коефіцієнт кореляції рівняння регресії
можна записати в наступному вигляді:
Із цих рівнянь видно, що обидві прямі регресії проходять через точку з координатами (а;в).
К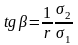
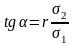 утові
коефіцієнти прямих регресії відповідно
дорівнюють:
утові
коефіцієнти прямих регресії відповідно
дорівнюють:
О скільки
т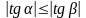 о
о
ч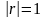 им
ближче r
до
1, тим менший кут між
прямими
регресії. Ці прямі зливаються тільки
тоді, коли
им
ближче r
до
1, тим менший кут між
прямими
регресії. Ці прямі зливаються тільки
тоді, коли
При r=0 прямі регресії набирають вигляду y=b; x=a
