Абстрактное определение булевых функций.

1) Множество элементов с заданным на нем операциями конъюнкции, дизъюнкции и одноместной операции отрицания называется булевой алгеброй если выполнены аксиомы где используются произвольные элементы множеств.

Аксиома - истина не требующая доказательств.

Джордж Буль изобрел своеобразную алгебру - систему обозначений и правил применимую ко всевозможным объектам от чисел до предложений. Пользуясь этой системой он мог закодировать высказывание с помощью символов своего языка, а затем манипулировать ими подобно тому как в математике манипулируют числами.

Основными операциями Булевой алгебры являются - конъюнкция, дизъюнкция, отрицание.

Базовым понятием Булевой алгебры является понятие высказывания под которым понимается любое утверждение рассматриваемое только с точки зрения его истинности или ложности.

В Булевой алгебре не существует истинно-ложных или ложно-истинных высказываний. Высказывание можно рассматривать как логическую переменную которая может быть истинной или ложной.

Исчисление высказываний какраз основано на том что их можно рассматривать как двоичные переменные которые могут принимать одно из 2 своих значений.

Высказывание называется простым если значение его истинности не зависит от значений истинности других высказываний, и сложным если его значение зависит от других высказываний.

Сложное высказывание можно рассматривать как логическую функцию зависящую от простых высказываний и принимающих также 2 значения.

Булева алгебра.

Булевой алгеброй называется произвольная множества элементов для которых определены две операции: сложения и умножения, сопоставляющие каждым 2 элементам A и B, их сумму A+B и произведение А*В; определена операция отрицания сопоставляющая каждому элементу А новый элемент -А имеются два особых элемента 0, 1 и выполняются следующие правила: (У вани скопируй дальше)

а	b	a	a^b	avb	a→b	a↔b
0	0	1	0	0	1	1
0	1	1	0	1	1	0
1	0	0	0	1	0	0
1	1	0	1	1	1	1

Логические действия можно заменить на арифметические:

	Отрицание	1-А
^	Конъюнкция	a*b or ab
v	Дизъюнкция	a+b - a*b, a+b-ab
→	Импликация	1-a+a*b; 1-a+ab
↔	Эквиваленция	1-(a-b)*(a*b)

a^b~m+n(a, b)

a v b ~ ma*(a, b)

26.11.13.

Задача №1

Трое друзей, болельщиков автогонок "Формула-1", спорили о результатах предстоящего этапа гонок. — Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.  — Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник.  — А об Алези и говорить нечего, ему не быть первым.  Питер, к которому обратился Ник, возмутился:  — Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.  По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?

Ответ: первым придет Шумахер

№2

В симфонический оркестр приняли 3 -ч музыкантов Брауна Смита и Вессона, умеющих играть на скрипке , флейте , альте , кларнете, гобое и трубе. Известно что : 1) Смит самый высокий 2) Играющий на скрипке меньше ростом играющего на флейте 3) Играющие на скрипке и флейте и Браун любят питцу 4) Когда между альтистом и трубачем возникает сора Смит мирит их 5) Браун не умеет играть ни на трубе ни на гобое. На каких инструментах играет каждый из музыкантов если каждый владеет 2 инструментами.

	скрипка	флейта	альт	кларнет	гобой	труба
Смит	0	1	0	0	1	0
Браун	0	0	1	1	0	0
Вессон	1	0	0	0	0	1

№3

Три одноклассника Влад Тимур и Юра встретились спустя 10 лет после окончания школы. Выяснилось что один из них стал врачом, другой физиком а 3 юристом. Один полюбил туризм, другой бег, а третий регби. Юра сказал что на туризм ему не хватает времени, хотя его сестра единственный врач в семье заядлый турист. Врач сказал что он разделяет увлечения коллеги. Забавно но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен. Определите кто чем любит заниматься в свободное время и какая у него профессия.

	Влад	Тимур	Юра
Врач	0	1	0
Физик	0	0	1
Юрист	1	0	0
Туризм	0	1	0
Бег	0	0	1
регби	1	0	0

27.11.13.

1) 111001,11₂ =57,75₁₀

111001 = 1*2⁵+1*2⁴+1*2³+0*2²+0*2¹+1*2⁰=32+16+8+1=48+9=57₁₀

11=1*2^-1+1*2^-2=0,5+0,25=0,75₁₀

2) 7521₈=7*8³+5*8²+2*8¹+1*8⁰=3584+320+16+1=3921₁₀

3) ABC35₁₆=10*16⁴+11*16³+12*16²+3*16¹+5*16⁰=655360+45056+3072+48+5=703541₁₀

4) 452₆+6544₇=2511₁₀

452₆=4*6²+5*6¹+2*6⁰=144+30+2=144+32=176₁₀

6544₇=6*7³+5*7²+4*7¹+4*7⁰=2058+245+28+4=2335₁₀

176₁₀+2335₁₀=2511₁₀

5 ) (A^B)↔(AvB)^A

A	B	Не А	Не B	A^B	Не(А^B)	(AvНеB)	(A^B)↔(AvB)	(A^B)↔(AvB)^A
0	0	1	1	0	1	1	1	1
0	1	1	0	0	1	0	0	0
1	0	0	1	0	1	1	1	0
1	1	0	0	1	0	1	0	0

6) neAv(B^C)

A	B	C	neA	B^C	Выраж.
0	0	0	1	0	1
0	0	1	1	0	1
0	1	0	1	0	1
0	1	1	1	1	1
1	0	0	0	0	0
1	0	1	0	0	0
1	1	0	0	0	0
1	1	1	0	1	1

15.01.14

Предикатом называется предложение, содержащее одну или несколько переменных, при подстановке в которые конкретных значений, предложение обращается в высказывание.

В предикатах переменные могут присутствовать явно или неявно, т.е. подразумеваться по смыслу.

Примеры: X>10; 3х⁴-5x < 30

Предикаты по количеству переменных, содержащихся в них, называются одно местными, двух местными, … n-местными предикатами.

Предикаты обозначаются: A(x), D(x; y) и др.

Например:

A(x), D(х,y)

Для каждого предиката можно указать область определения и множество истинности.

Областью определения предиката называется множество, элементы которого могут быть подставлены в предикат.

Множеством истинности предиката вызывается множество, элементы которого подставленные в предикат, обращают его в истинное высказывание. Если особо не оговорено, то принято обозначать множество истинности предиката буквой Т с индексами или без таковых.

Если некоторое множество X – область определения предиката, а множество T - множество его истинности, то, очевидно, что множество T - подмножество множества X, ТХ

Область определения и множество значений предиката либо задаются заренее, либо предлагается установить.

Алфавит исчисления предикатов.

1. A, B, C, D …Z, Y, X – обозначение предикатов (с индексами или без таковых)

2. x, y, z, … обозначение переменных (с индексами или без таковых)

3. x₀ , y₀ , z₀ – постоянные значения, константы

4. , ,  , , , ,  и другие символы логических операций и теории переносятся без изменения в исчисление предикатов.

5  - квантор общности и  - квантор существования

6. Могут использовать иные, заранее оговоренные или интуитивно понятные символы.

Язык логики предикатов.

Каждому предикату присваивается имя.

Предикаты могут быть поротыми и составными. Составные предикаты образуются из простых предикатов с помощью логических связок по правилам алгебры логики.

Из двух предикатов можно образовать новый предикат, который часто называется высказывательной формой.

Высказывательные формы могут входить в предикат и при этом они называются предикаторами или препозиционными функциями.

Примеры высказывательных форм

Рассмотрим двуместную высказывательную форму: x  y+2. Пусть x определено на множестве M_x ={3;5}, y – на множестве M_y={1;5;8}. Этой форме соответствуют два предиката. Один P_{1 -} задан на множестве, образованным декартовым произведением X₁= M_x x M_y

Другой P_{2 -} задан на множестве, образованным декартовым произведением X₂= M_y x M_x

Это значит, что двуместной высказывательной форме соответствует два предиката. Чтобы установить взаимно-однозначное соответствие между ними, на установит линейный порядок с помощи отношения "предшествует". Порядок может определять алфавитом и (или) индексами при переменных, располагая их в порядке возрастания.

Принято называть:

1. Одноместный предикат – свойством (предикат - свойство).

2. Двуместный, трехместный, … , n-местный предикат – отношением (предикат – отношение)

3. Нульместный предикат – высказыванием.

Тождественно – истинным называется предикат, который принимает истинное значение на всей области определения ( множество истинности совпадает с областью определения)

Тождественно – ложным называется предикат, который принимает ложное значение на всей области определения (множество истинности пустое).

29.04.14

Нормальные формы являются синтаксически однозначным способом записи формулы, реализующей заданную функцию.

Если х - логическая переменная, а σ{0,1} то выражение

или ,         0если x 1 если x x          x если 0 x если 1 x

называется литерой. Литеры x и x называются контрарными. Конъюнктом называется конъюнкция литер. Дизъюнктом называется дизъюнкция литер. Например, формулы являются конъюнктами, формулы - дизъюнктами, а формула является одновременно и конъюнктом и дизъюнктом. x x y x и z y x      x y x и z y x     z x 

Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция конечного числа конъюнктов.

Конъюнктивной нормальной формой (КНФ) называется конъюнкция конечного числа дизъюнктов.

Более просто: ДНФ - это сумма произведений, а КНФ - это произведение логических сумм

Любая булева функция может иметь бесконечно много представлений в виде ДНФ и КНФ.

Совершенные нормальные формы

Если в каждом члене нормальной формы представлены все переменные (либо сами, либо их отрицания), причем в каждом отдельном конъюнкте или дизъюнкте любая переменная входит ровно один раз (либо сама либо ее отрицание), то эта форма называется совершенной нормальной формой (СДНФ или СКНФ).

П римеры: Пусть задана функция трех переменных f(x,y,z).

Теорема

1. Любая булева функция, не являющаяся тождественным нулем, имеет только одну СДНФ, с точностью до расположения членов.

2. Любая булева функция, не являющаяся тождественной 1, имеет только одну СКНФ, с точностью до расположения членов.

ДНФ – дизъюнктивной нормальной формой

КНФ – конъюнктивной нормальной формой

СДНФ – совершенной дизъюктивной формой

СКНФ – совершенной коньюктивной формой.

05.02.14

Две формулы,   и   логики предикатов называются равносильными на множестве  , если при любой подстановке в эти формулы вместо предикатных переменных любых конкретных предикатов, определенных на  , формулы превращаются в равносильные предикаты.

Приведем пример двух неравносильных формул логики предикатов

2(а+b)=2a+2b

 есть "  — четно"

 есть "  — нечетно"

Определение 2. Приведенной формой для формулы логики предикатов называется такая равносильная ей формула, в которой из операций алгебры высказываний имеются только операции  , причем знаки отрицания относятся лишь к предикатным переменным и к высказываниям.

Теорема. Для каждой формулы логики предикатов существует приведенная форма.

Определение 3. Предваренной нормальной формой для формулы логики предикатов называется такая ее приведенная форма, в которой все кванторы стоят в ее начале, а область действия каждого из них распространяется до конца формулы.

Теорема. Для каждой формулы логики предикатов существует предваренная нормальная форма.

Формула H логики предикатов называется логическим следствием формулы  , если при всякой интерпретации, при которой   превращается в тождественно истинный предикат, формула H также превращается в тождественно истинный предикат.

26.02.14

Построение полинома Жигалкина

 

 

 

0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	1
0	1	1	1	0
1	0	0	0	1
1	0	0	1	0
1	0	1	0	0
1	0	1	1	1
1	1	0	0	1
1	1	0	1	0
1	1	1	0	1
1	1	1	1	0

Построим для неё полином Жегалкина:

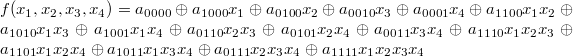
Так как  , то  . Далее подставляем все остальные наборы в порядке возрастания числа единиц, подставляя вновь полученные значения в следующие формулы:

Таким образом, полином Жегалкина выглядит так:

05.03.14

Методы Треугольника

Р 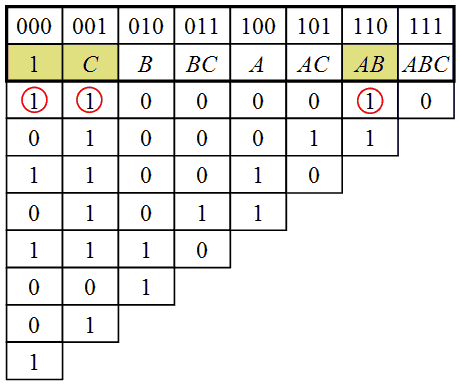ассмотрим этот метод для функции от 3 переменных P(a,b,с) (рисунок в тетради 1))

Чтобы получить формулу по которой расчитывается какой либо коэфициэнт, нужно из клетки которой он записан, пройтись всеми возможными путями влево до столбца Р таблицы истиности, делая ходы влево и влево вниз записать значения в конечных ячейках и сложить их все между собой по модулю.

Значит в 1 столбце сверху записан коэфициент а0 = Р(000), во втором столбце а1 = Р(000) + Р(001), в третьем а3 = Р (000) + Р (001)+ Р(010)= Р (000) + Р(010)

а3 = Р(000) + Р(001) + Р(100) = Р(000) + Р(101)+ Р(010)+Р(011)

12.03.14