Сложение и вычитание в сс.

1

+

+

+

+

) 11011₂ 2) 357₈ 3) 35АС7₁₆ 4) 101111₂

1101₂ 402₈ СД32₁₆ 111₂

101000₂ 761₈ 427F9₁₆ 1011₂

1000001₂

5

+

-

-

-

) 35АД,17₁₆ 6) 753₈ 7) 35АС7₁₆ 8) 11011₂

АВС,33₁₆ 264₈ СД32₁₆ 1101₂

4069,4А₁₆ 451₈ 28Д95₁₆ 1110₂

9

-

) 3578А,2С₁₆

СДЕ,F5₁₆

34AAB,37₁₆

5.11.13.

Сумматор двоичных чисел.

Полусумматор

A = 10110₂ B = 11011₂

A	B	P(перенос)	S(сумма)
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

P=A^B F₇ =

S = (AvB)^(A^B)

A	B	AvB	A^B	( A^B)	( AvB)^(A^B)
0	0	0	0	1	0
0	1	1	0	1	1
1	0	1	0	1	1
1	1	1	1	0	0

А

А

НЕ

НЕ

а

b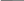

ИЛИ

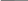
В

И

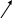
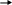
В

ИЛИ

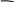
Это полусумматор двоичных чисел так как реализует суммирование одноразрядных двоичных чисел без учета переноса из младшего разряда.

Сумматор - это электронная логическая схема выполняющая суммирование двоичных чисел. Полный одноразрядный сумматор должен иметь 3 входа (2 слагаемых и перенос из младшего разряда) и два выхода (сумму и перенос).

Полусумматор

А

В

Р₀

S

Р₀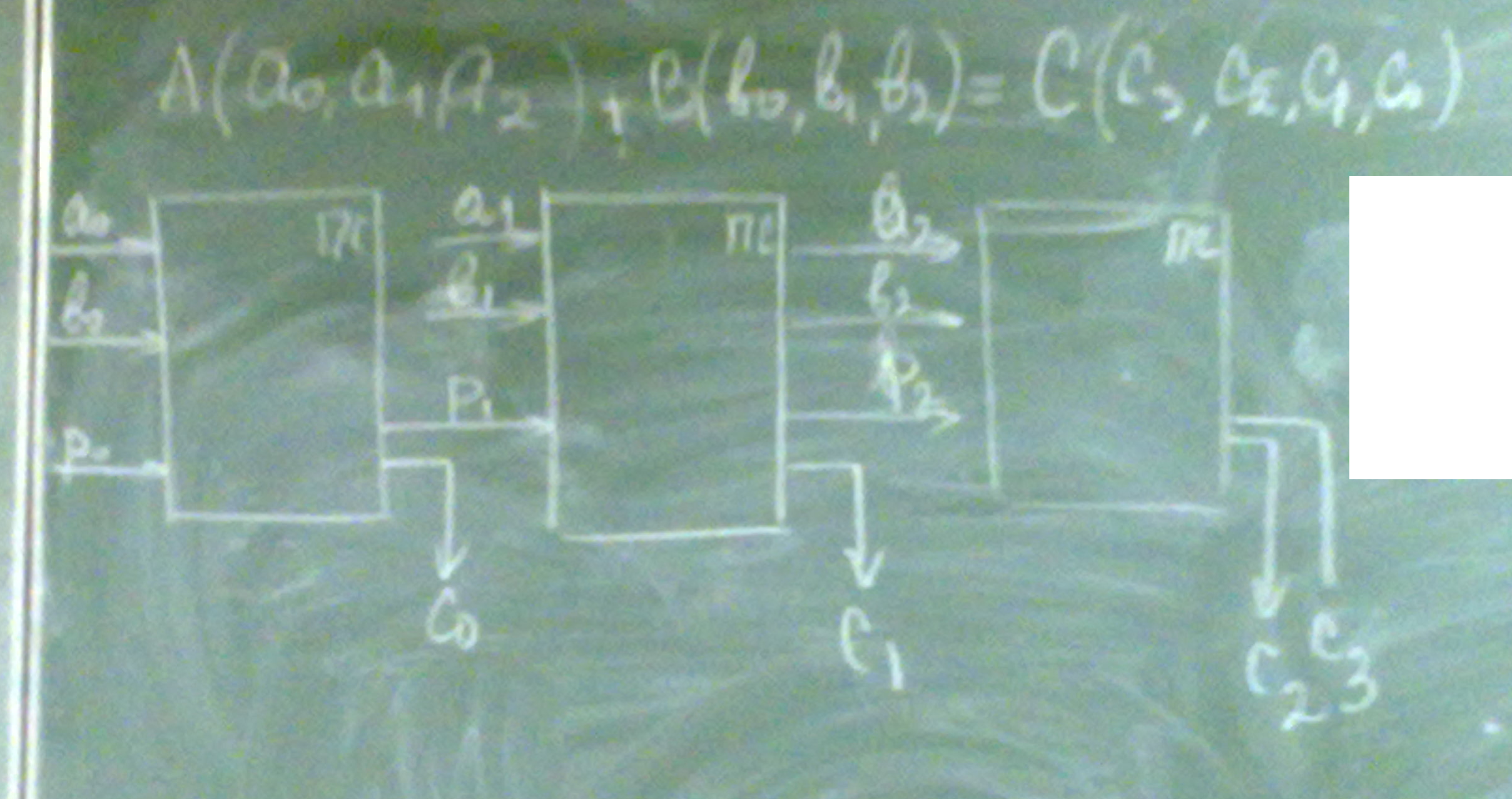

Как работает сумматор на примере A = 1 0 1 1 0₂ B = 1 1 0 1 1₂

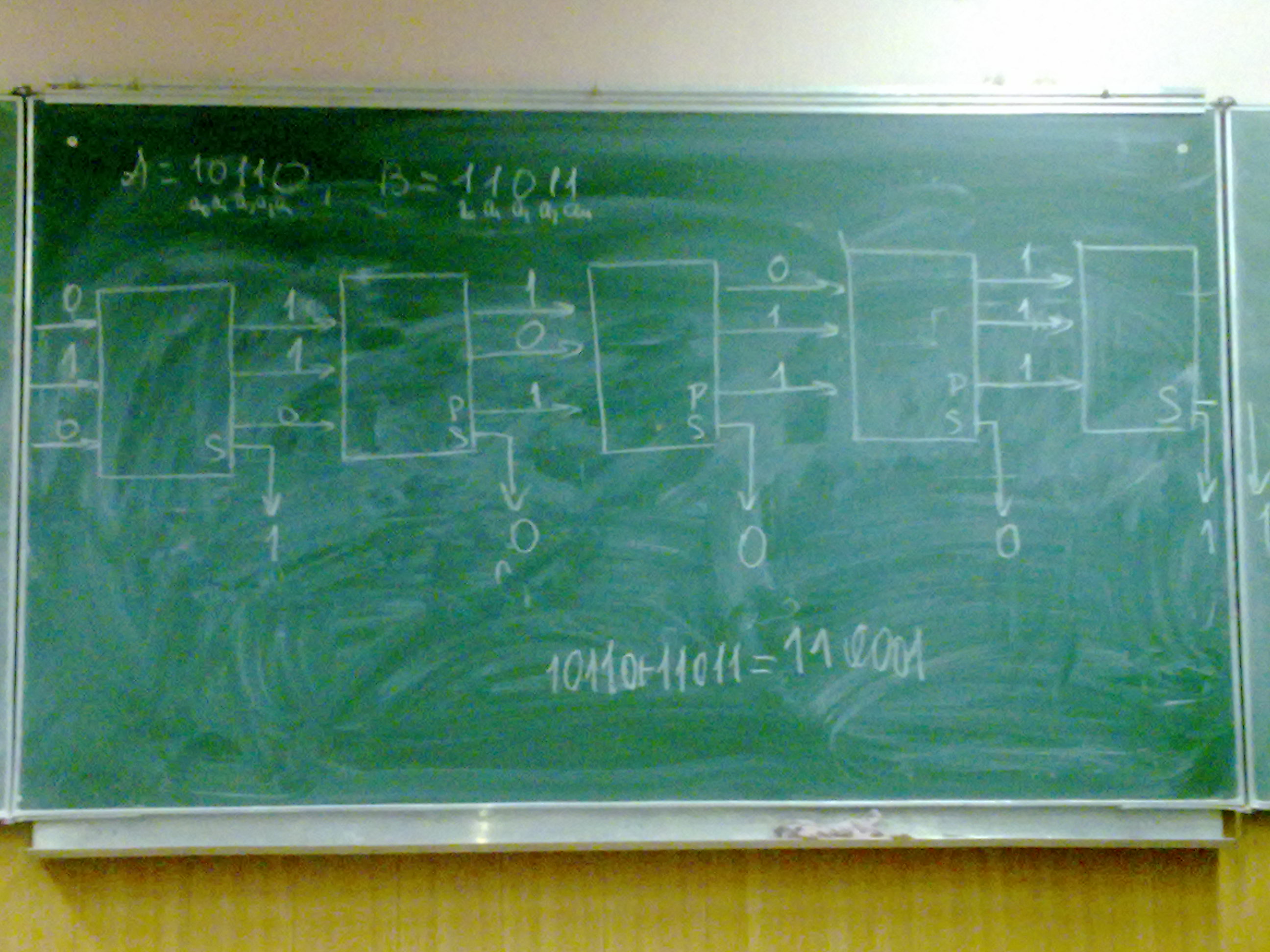
Триггер.

Важнейшей структурной единицей оперативной памяти, а так же внутренних регистров процессора является триггер. Это устройство позволяет запоминать, хранить и считывать информацию. Каждый триггер может хранить 1 бит информации. Самый распространенный тип триггера - это RS триггер. Он имеет 2 входа и 2 выхода.

S

0 1

1 0

e

QQ

S	R	Q	Q
0	0	запрет
0	1	1	0
1	0	0	1
1	1	Хранение бита

НЕ

S

R

1

ИЛИ

ИЛИ

НЕ

Q

0

1

0

1

12.11.13.

Умножение в различных системах счисления.

*	0	1
0	0	1
1	0	1

В двоичной системе умножение:

В восьмеричной:

*	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7
2	0	2	4	6	10	12	14	16
3	0	3	6	11	14	17	22	25
4	0	4	10	14	20	24	30	34
5	0	5	12	17	24	31	36	43
6	0	6	14	22	30	36	44	52
7	0	7	16	25	34	43	52	61

13.11.13.

Булева алгебра.

1) Булева функция:

Переменная X называется булевой если она способна принимать только 2 значения 0 и 1.

Функция f(x₁, x₂.... x_n) называется булевой (логической или функцией алгебры логики или переключательной) если все её аргументы являются булевыми, а сама функция может принимать значения 0 и 1.

Множество всех булевых функций обозначают через P с индексом 2 {f(x₁), f(x₂), f(x₃)} = P₂

Способы задания булевых функций:

1 ) Табличный - это таблица истинности

2) Графический - логические и переключательные схемы.

3) Аналитический - с помощью логической формулы

Б улева функция от n элементов в дискретной математике - это отображение множество Bⁿ B, где В = {0,1} - булево множество.

Не отрицательное целое число n называют АРНОСТЬЮ или местностью функции.

Элементы декартового произведения Bⁿ называют булевыми векторами. Множество всех булевых функций от любого числа аргументов обозначается P₂, а от n аргументов P₂(n). Переменные принимающие значения из булевого множества называются булевыми переменными.

При работе с булевыми функциями происходит полное абстрагирование от содержательного смысла который имелся в виду в алгебре высказываний. Тем немение между булевыми функциями и формулами алгебры высказываний можно установить взаимно-однозначное соответствие если:

1) Установить взаимно-однозначное соответствие между булевыми переменными и пропозициональными переменными.

2) Установить связь между булевыми функциями и логическими связками, оставить расстановку скобок без изменений.

19.11.13.

Каждая булева функция Арности "n" полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длинны n.

Число таких векторов = 2ⁿ. Поскольку на каждом векторе булева функция может принимать значение либо 0, либо 1, то количество всех n-арных булевых функций равно 2²ⁿ.

Булева функция задается конечным набором значений что позволяет представить её в виде таблицы истинности.

X1	X2	...............	Xn-1	xn	F(x1, x2,..., xn)
0	0	...............	0	0	0
0	0	...............	0	1	0
0	0	...............	1	0	1
0	0	...............	1	1	0
..................................................................................................................
1	1	...............	0	0	1
1	1	...............	0	1	0
1	1	...............	1	0	0
1	1	...............	1	1	0

Примеры булевых функций:

1) При n=0 количество булевых функций сводится к 2. Первая из них тождественно равна 0 а вторая 1. Это НУЛЬАРНЫЕ функции. (Булевы константы)

Значения	Обозначения	Н Нуль-арные функции азвания
0	F(0;0)=0	Т ождественный нуль
1	F(0;1)=1	Тождественная единица

2) Унарные функции.

При n=1 число булевых функций равно 4.

X0=x	1	0	обозначения	Название
0	0	0	F(1;0)=0	Тождественный нуль
1	0	1	F (1;1)=x=x=x1=Not(x)	Отрицание, логическое "нет", "не", "ни", инвертор, обмен.
2	1	0	F(1;2)=x	Тождественная функция, логическое "да", повторитель
3	1	1	F(1;3)=1	Тождественная единица.

3) Бинарные функции.

При n=2 число булевых функций равно 16.

		0	*	→'	x	←'	y	+	v	↓	↔	y'	←	x'	→	|	1
x	y	g0	g1	g2	g3	g4	g5	g6	g7	g8	g9	g10	g11	g12	g13	g14	g15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

' - это отрицание. | - это штрих Шеффера. v - стрелка Пирса.

g ₈(x;y)= g₇=x↓y

g₆(x;y)=x+y -сумма Жигалкина.

4) Тернарные функции.

При n=3 число булевых функций равно 256.

Две булевы функции F(x;y) и G(x;y) называются равными если каждому набору значений аргументов x, y обе функции сопоставляют один и тот же элемент из множества 0, 1.

XvY=YvX.

Булеву функцию можно выразить через конъюнкцию, дизъюнкцию и отрицание.

Лемма: "Для произвольной булевой функции F(x₁, x₂,..., x_n) справедливы следующие формулы называемые формулами разложения этой функции по переменной x₁:

f(x₁, x₂,..., x_n)=(x₁* f(1, x₂,..., x_n))v(x₁^'* f(0, x₂,..., x_n))

f(x₁, x₂,..., x_n)=(x₁v f(0, x₂,..., x_n))*(x₁^'v f(1, x₂,..., x_n))

Теорема: "Всякая булева функция f(x₁, x₂,..., x_n) может быть представлена в виде суперпозиции конъюнкции, дизъюнкции и отрицания; причем знак отрицания стоит только непосредственно около переменной и не стоит ни перед одной из внутренних скобок."

Булевы функции и формулы алгебры высказываний.

Надо установить соответствие между формулами алгебры высказываний и булевыми функциями:

1) Определяется взаимно однозначное соответствие между пропозициональными переменными и булевыми переменными.

2) Устанавливается соответствие между знаками логических связок и одноименных булевых функций.

Логические связки		^	v	→	↔
Булевы функции		*	v	→	↔

3) Скобкам остаются неизменными

Каждой формуле алгебры высказываний соответствует единственно булева функция и наоборот.

Пример:

( P↔Q)→(X₁vX₂)^Z

(p↔q')→(x₁'v x₂')*z'

Пример №2:

( АvB)→(A*B)v(AvB)

(a' v b)→(a^b')v(a' ^ b')

20.11.13.