50. Ток смещения. Система уравнений Максвелла. Относительность электрических и магнитных полей.

Уравнения Максвелла— система уравнений в дифференциальной или интегральной форме, которые описывают электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах

В дифференциальной форме уравнение Максвелла выглядит так

В интегральной форме уравнение Максвелла выглядит так

Ток смещения— величина, прямо пропорциональная быстроте изменения электрической индукции. В вакууме, а также в любом веществе, в котором можно пренебречь поляризацией либо скоростью её изменения, током смещения называется поток вектора быстроты изменения электрического поля через некоторую поверхность

Отдельное рассмотрение электрического и магнитного полей имеет относительный смысл. Так, если электростатическое поле создается системой неподвижных зарядов, по эти заряды, являясь неподвижными относительно одной инерциальной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. 

51. Понятия о колебательных процессах. Гармонические колебания (гк), их характеристики. Представление гк в аналитическом, графическом виде и с помощью векторных диаграмм.

Колебательные процессы широко распространены в природе и технике. Качание маятника часов, волны на воде, переменный электрический ток, свет, звук являются примерами колебаний различных физических величин. При движении маятника колеблется координата его центра тяжести. В случае переменного тока колеблются напряжение и ток в цепи. Эти два процесса качественно совершенно различны по своей физической природе. Однако количественные закономерности этих процессов имеют между собой очень много общего. Гармонические колебания— колебания, при которых физическая величина изменяется с течением времени по закону синуса и косинуса. Кинематическое уравнение гармонических колебаний имеет вид

Гармонические колебания можно представить несколькими способами

Аналитический x = A sin ( ω t + φ₀ )

Графический

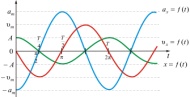
Геометрический

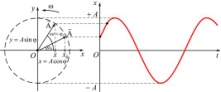
52. Дифференциальное уравнение гармонических колебаний. Гармонические осцилляторы: маятники, груз на пружине, колебательный контур. Энергетические соотношения для осцилляторов.

Обобщенное гармоническое колебание в дифференциальном виде

Сначала запишем уравнении динамики 2^ой закон Ньютона: И_теперь: Делим на m и обозначаем  : Это уравнение решается.

Гармони́ческий осцилля́тор—система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x . Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины.   . Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. . Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку_индуктивности и  конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения). Соотношения Мэнли — Роу — энергетические соотношения, характеризующие взаимодействие колебаний или волн в нелинейных системах с сосредоточенными или распределёнными параметрами.