4.5 Результаты расчета металлокаркаса

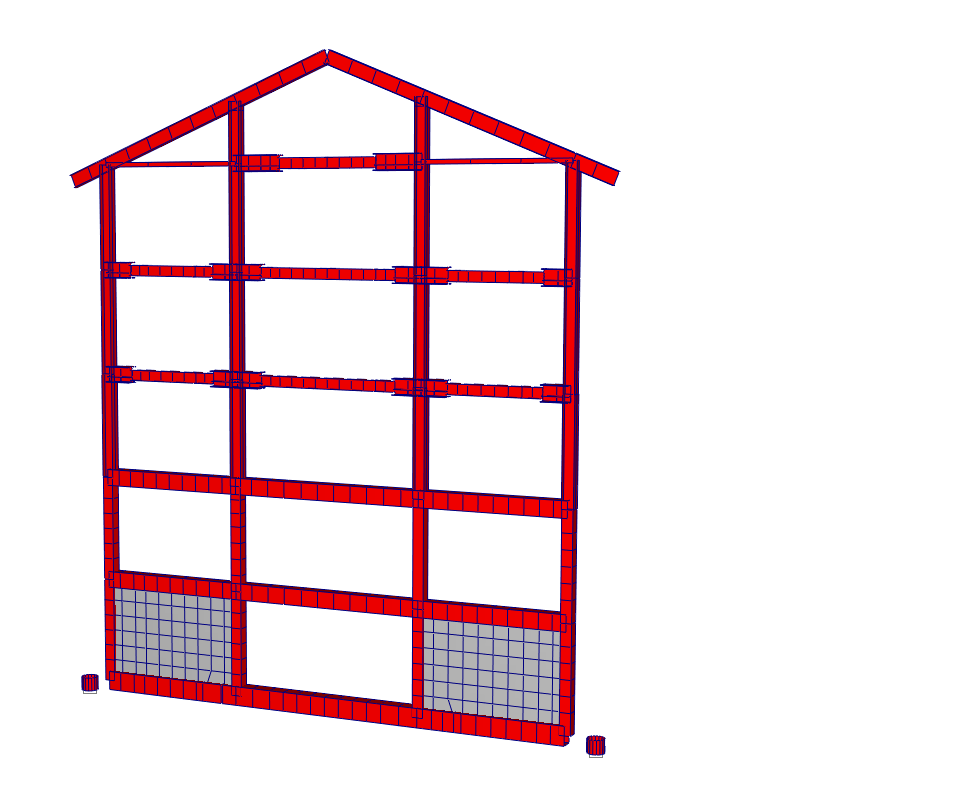
Рисунок 4.18 Общий вид расчетной схемы по оси 6

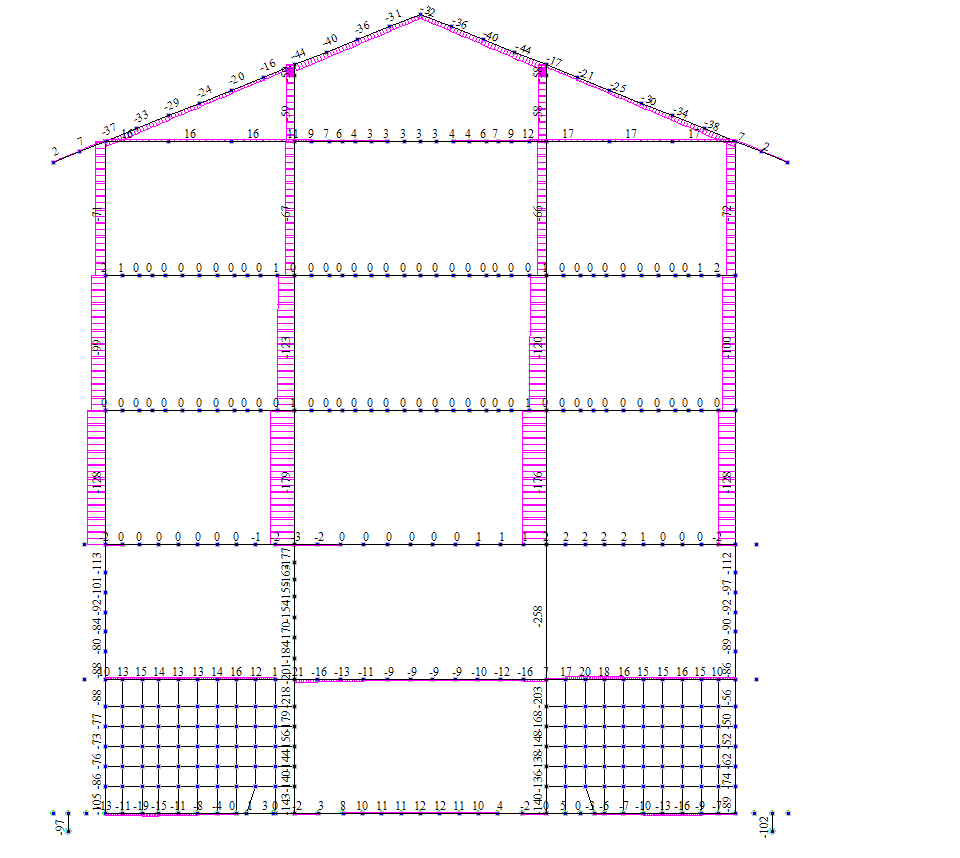
Рисунок 4.19 Статика. Ось 6. Эпюры продольных усилий N

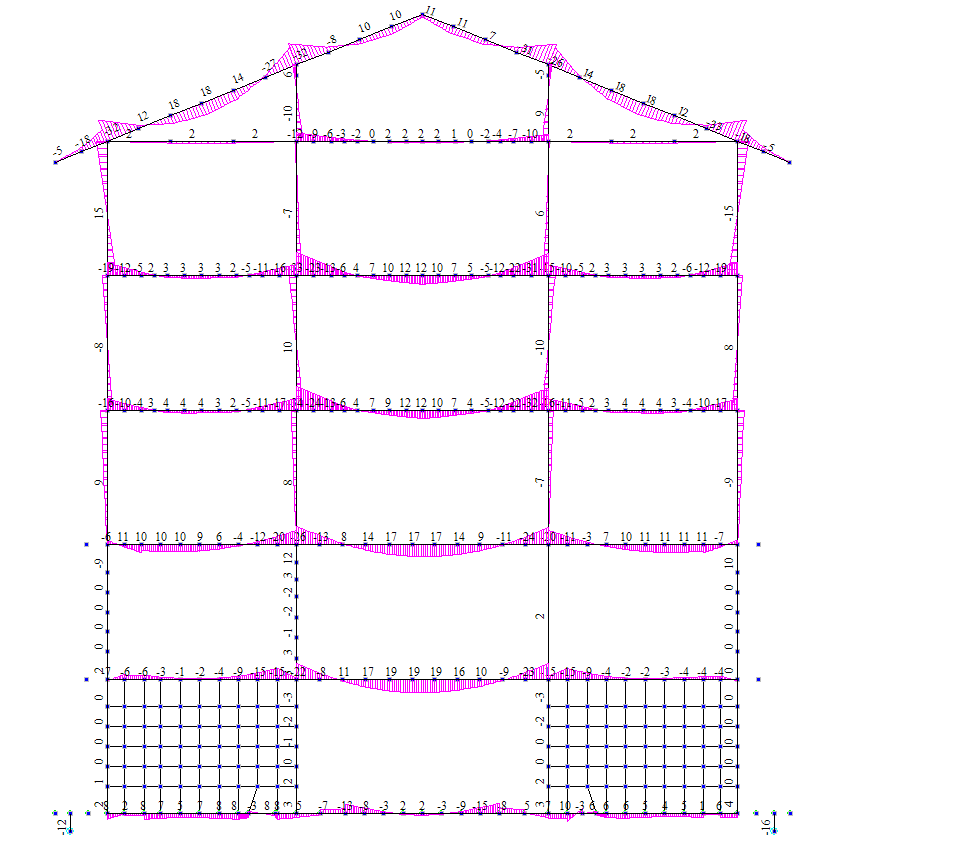
Рисунок 4.20 Статика. Ось 6. Эпюры изгибающих моментов М

Рисунок 4.21 Статика. Ось 6. Эпюры поперечных усилий Q

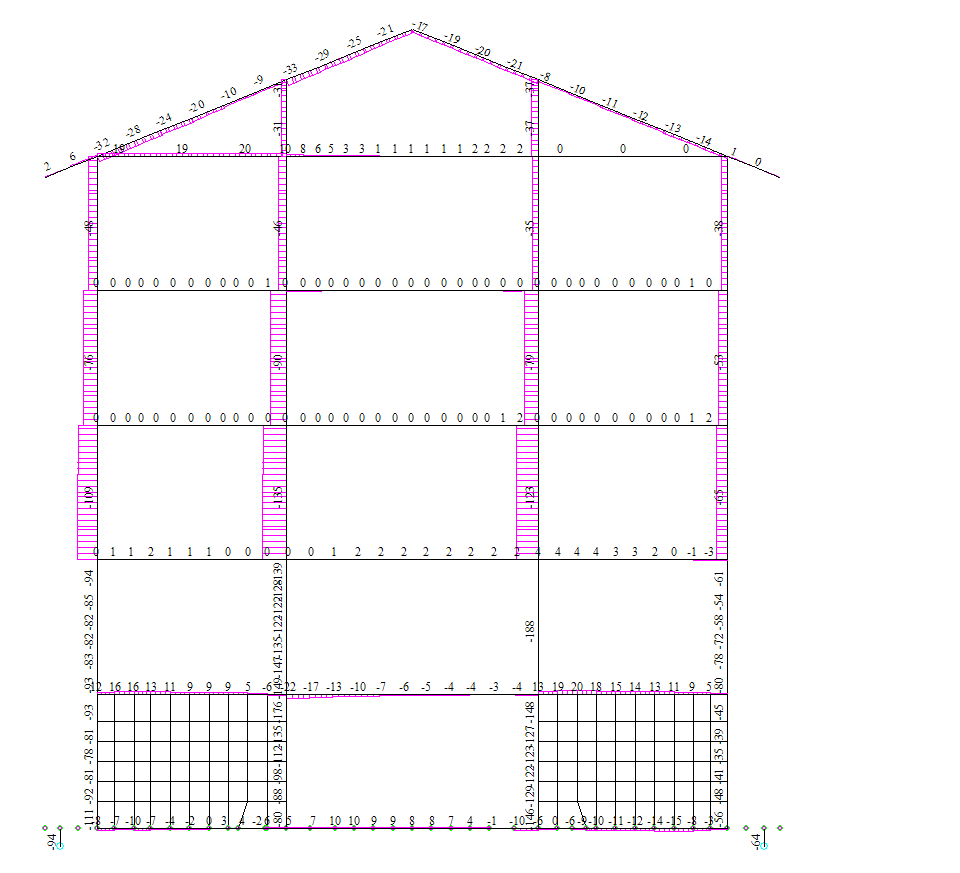
Рисунок 4.23 Сейсмика +Y. Ось 6. Эпюры продольных усилий N

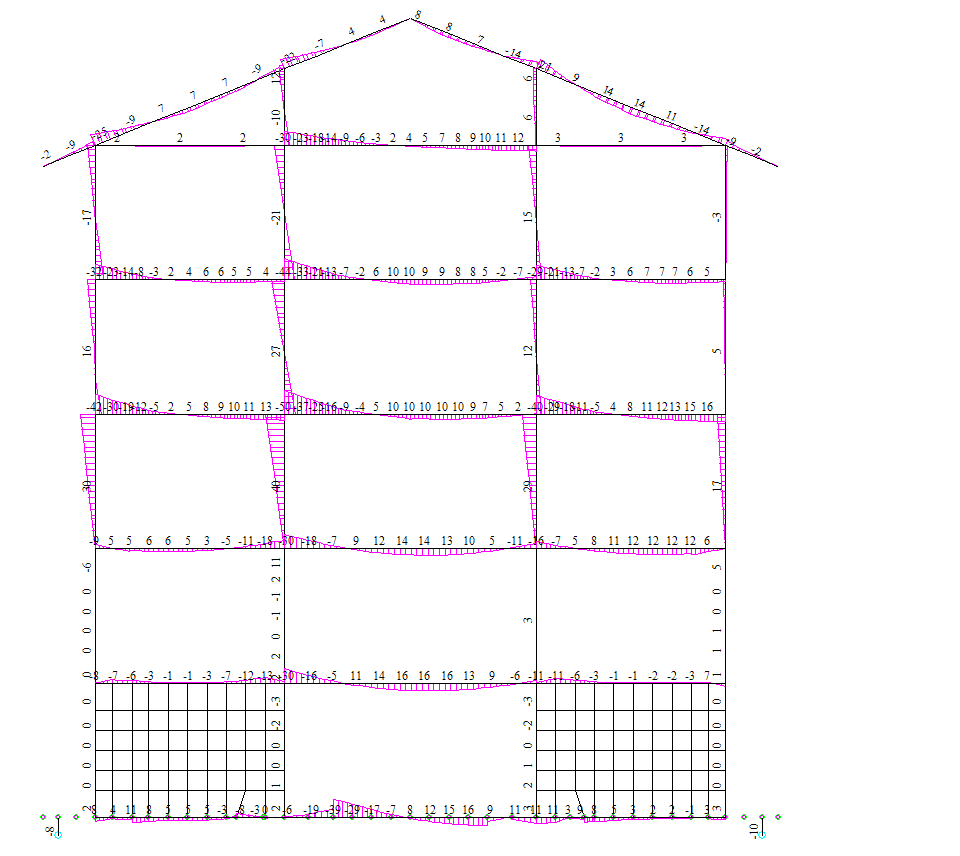
Рисунок 4.24 Сейсмика +Y. Ось 6. Эпюры изгибающих моментов М

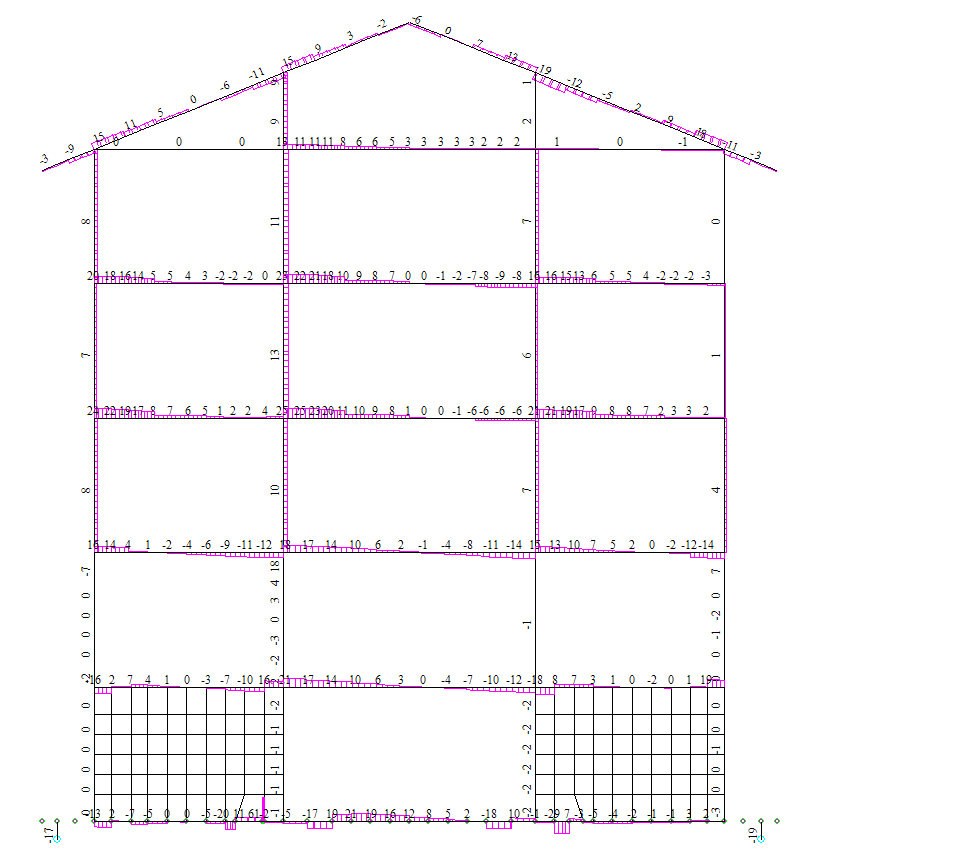
Рисунок 4.25 Сейсмика +Y. Ось 6. Эпюры поперечных усилий Q

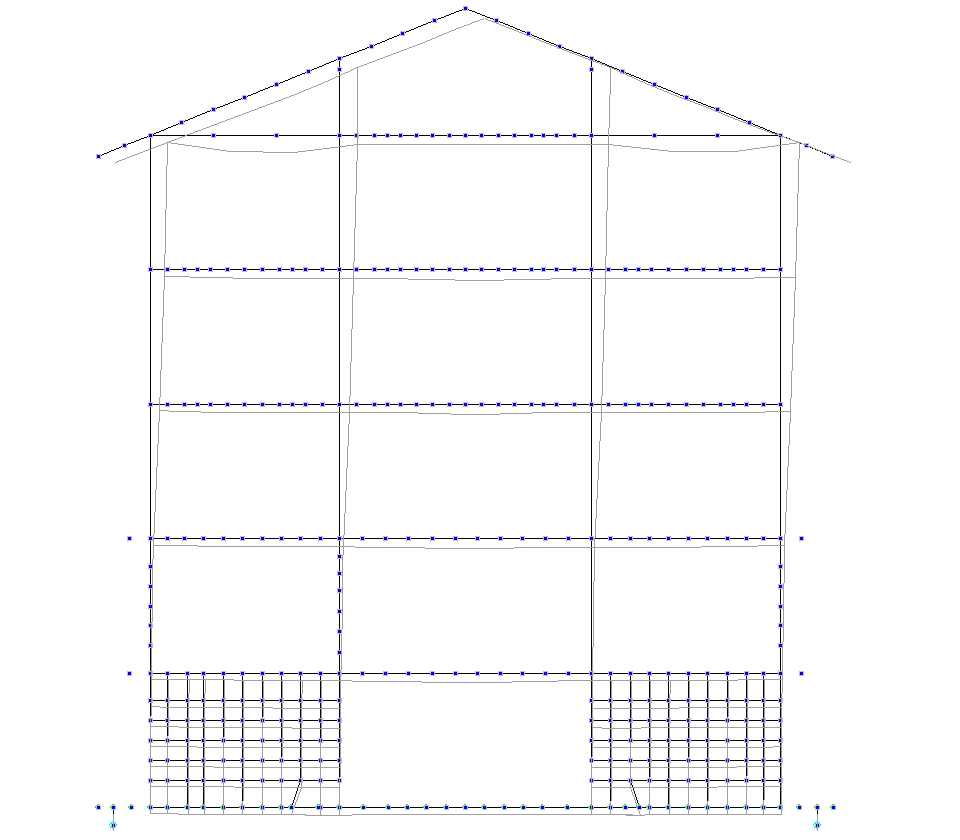
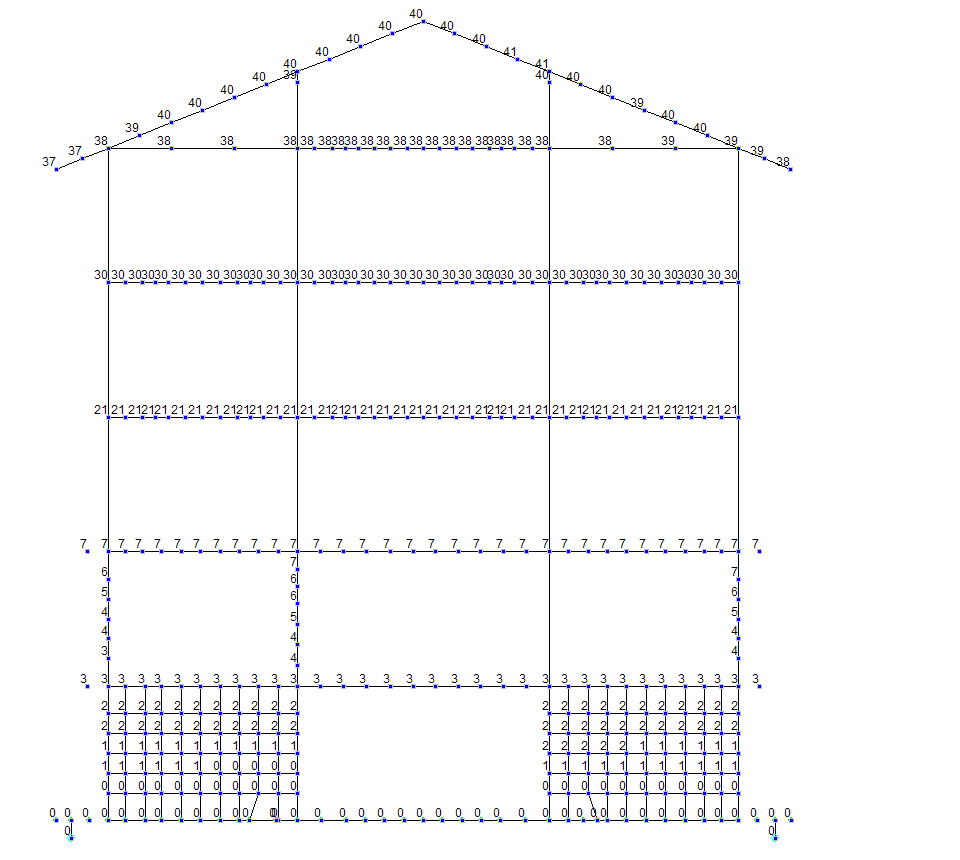
Рисунок 4.26 Сейсмика +Y. Ось 6. Деформации Y

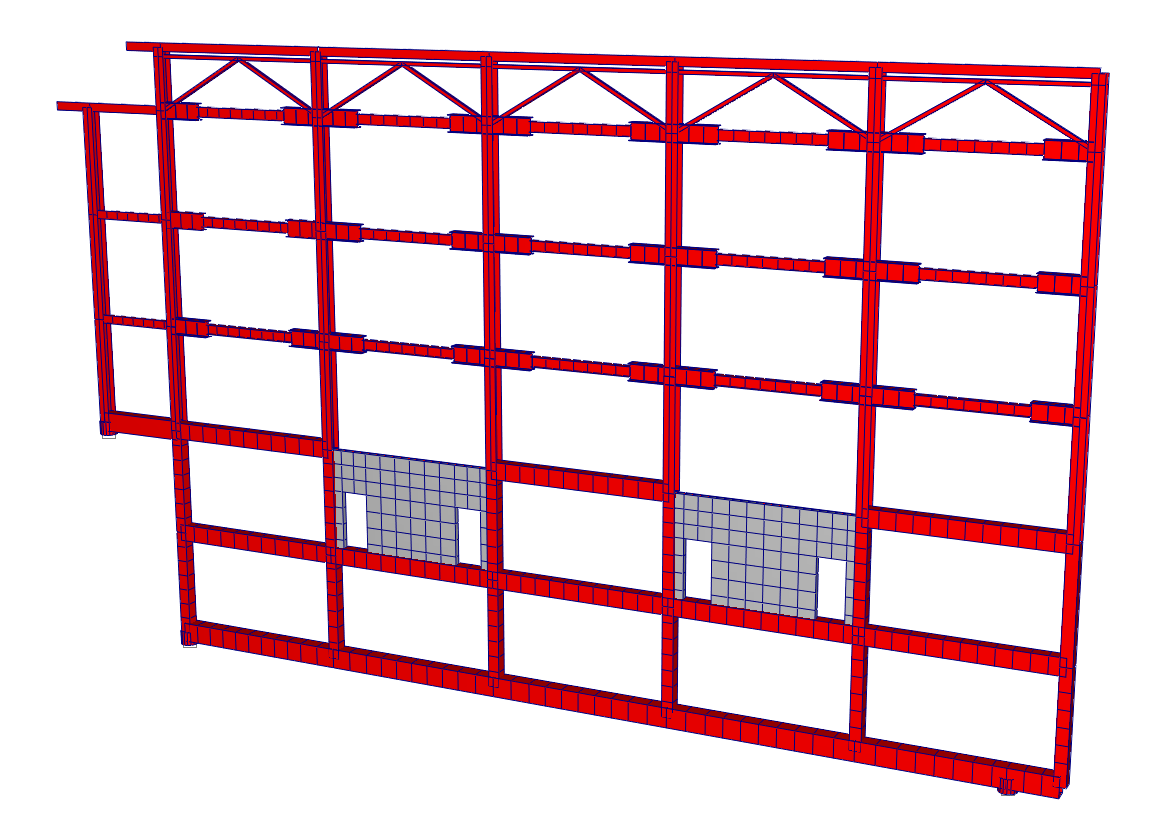
Рисунок 4.27 Общий вид расчетной схемы по оси Б

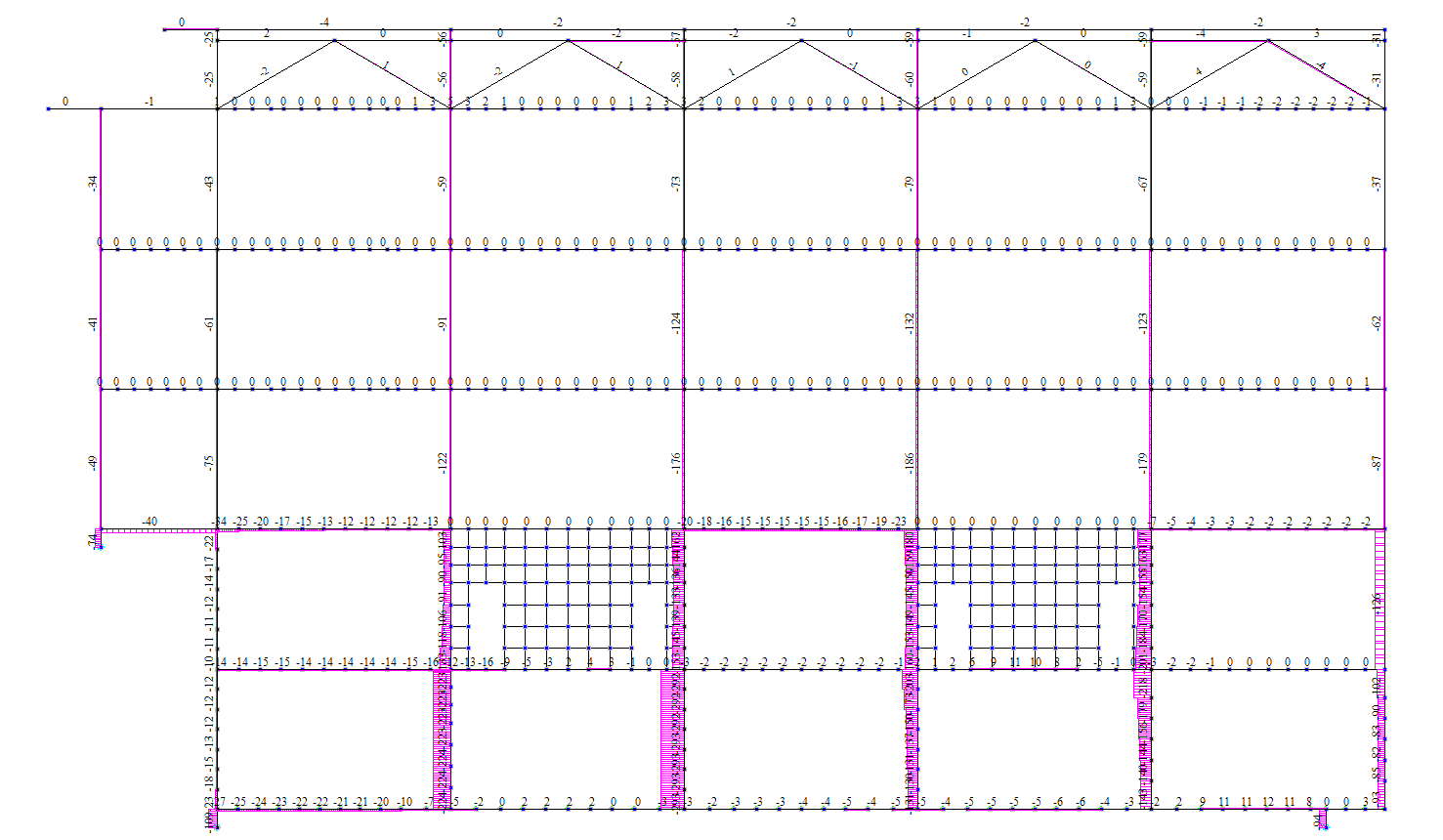
Рисунок 4.28 Статика. Ось Б. Эпюры продольных усилий N

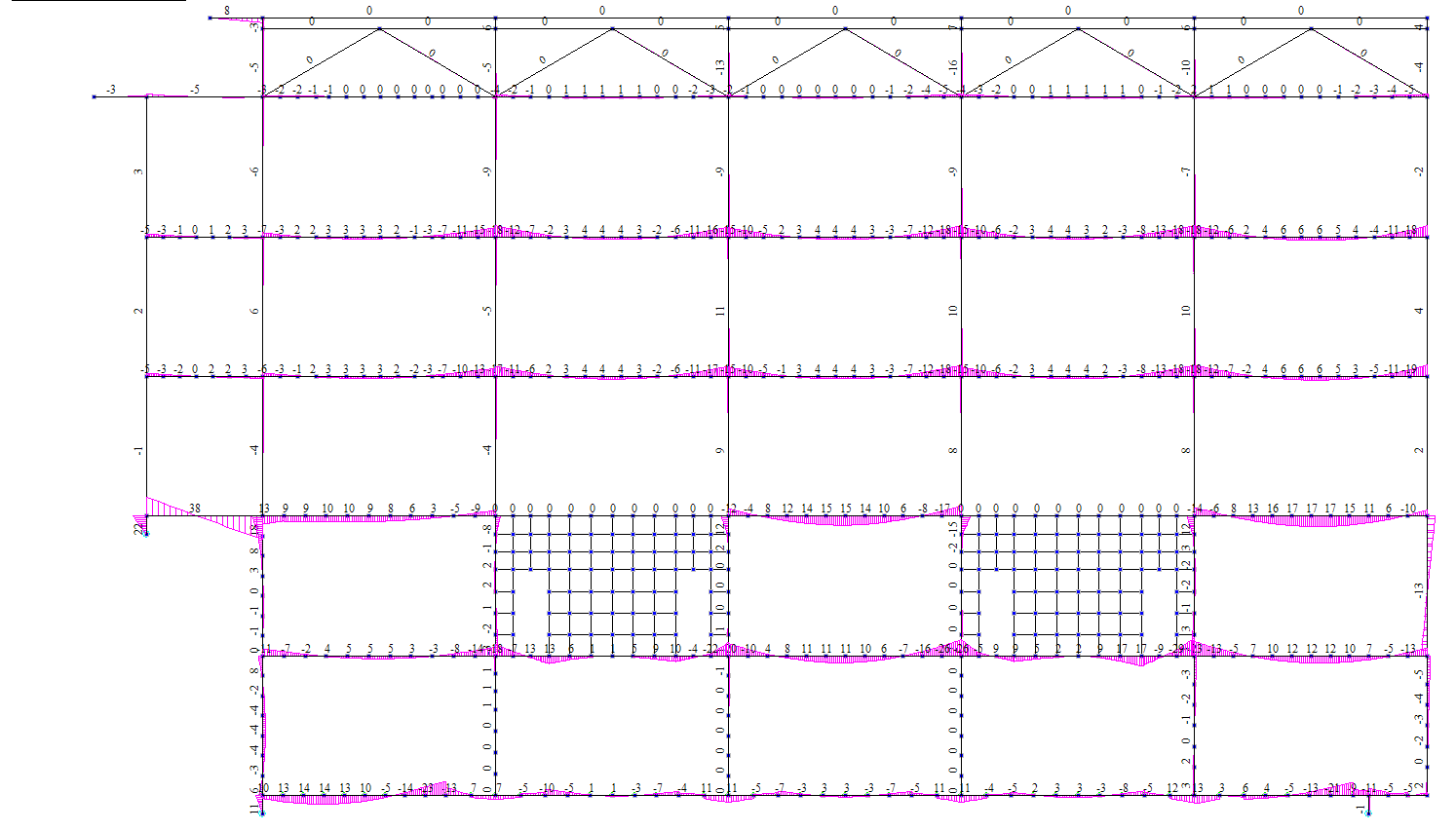
Рисунок 4.29 Статика. Ось Б. Эпюры изгибающих моментов М

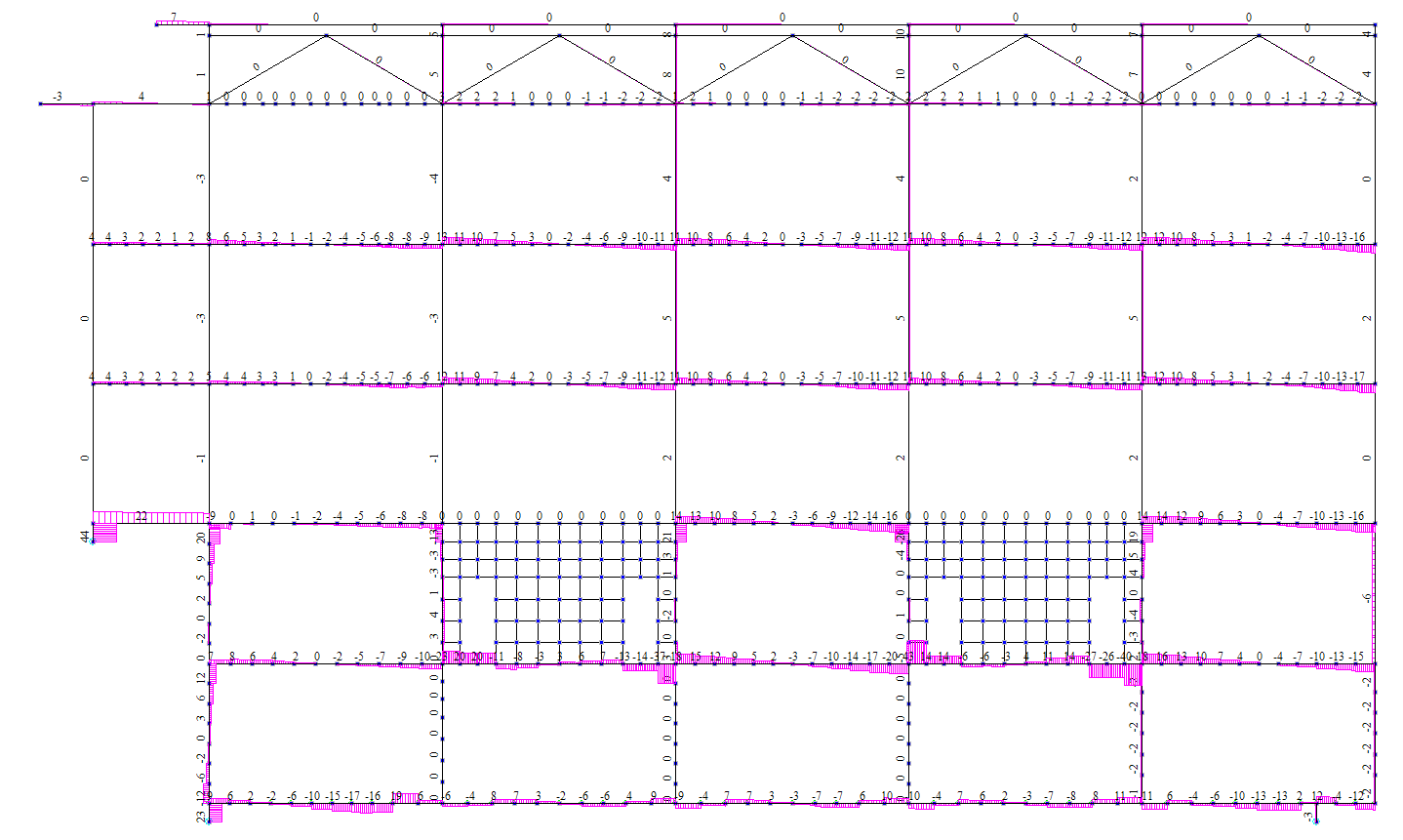
Рисунок 4.30 Статика. Ось Б. Эпюры поперечных усилий Q

Рисунок 4.31 Сейсмика +Х. Ось Б. Эпюры продольных усилий N

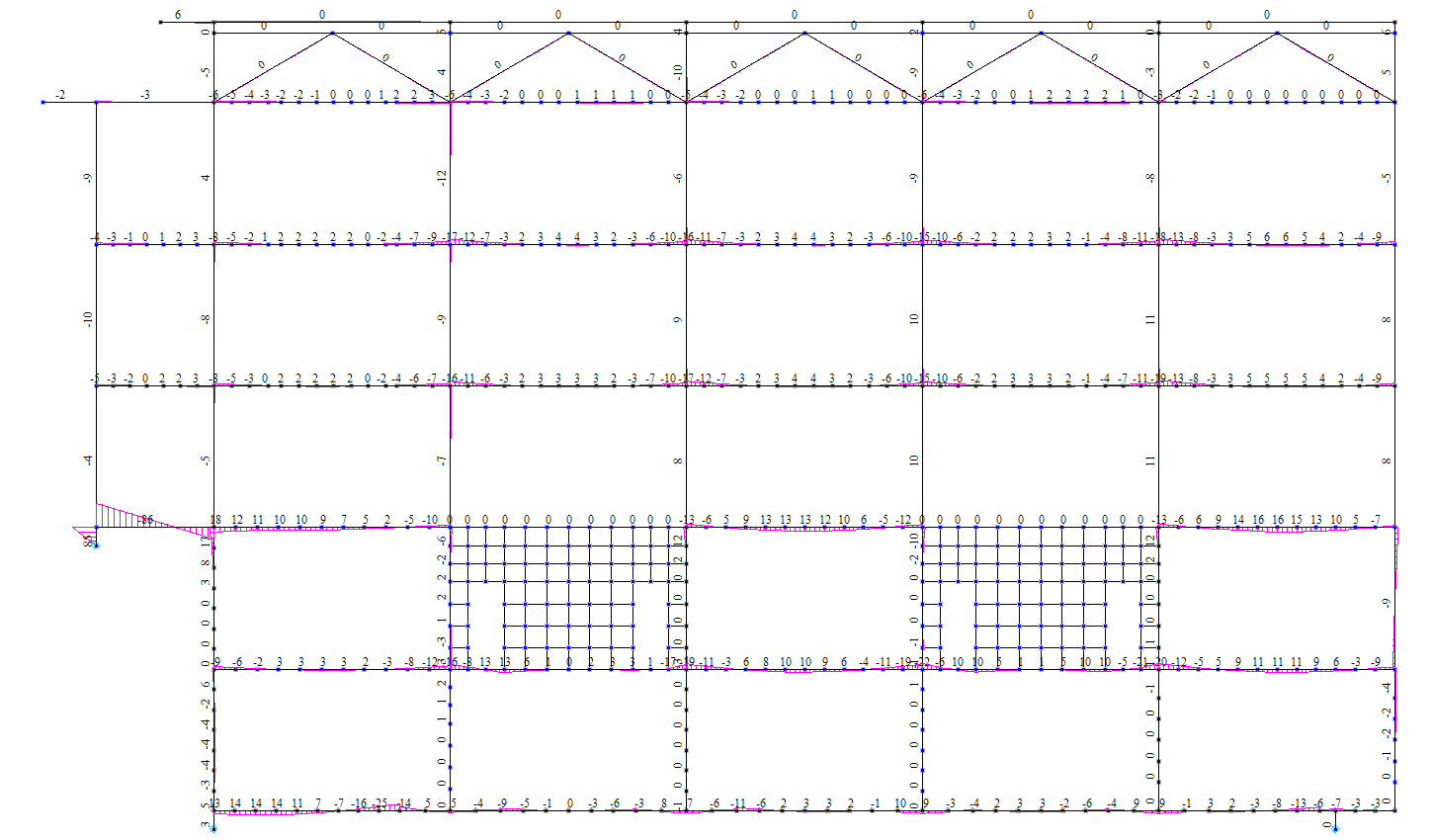
Рисунок 4.32 Сейсмика +Х. Ось Б. Эпюры изгибающих моментов М

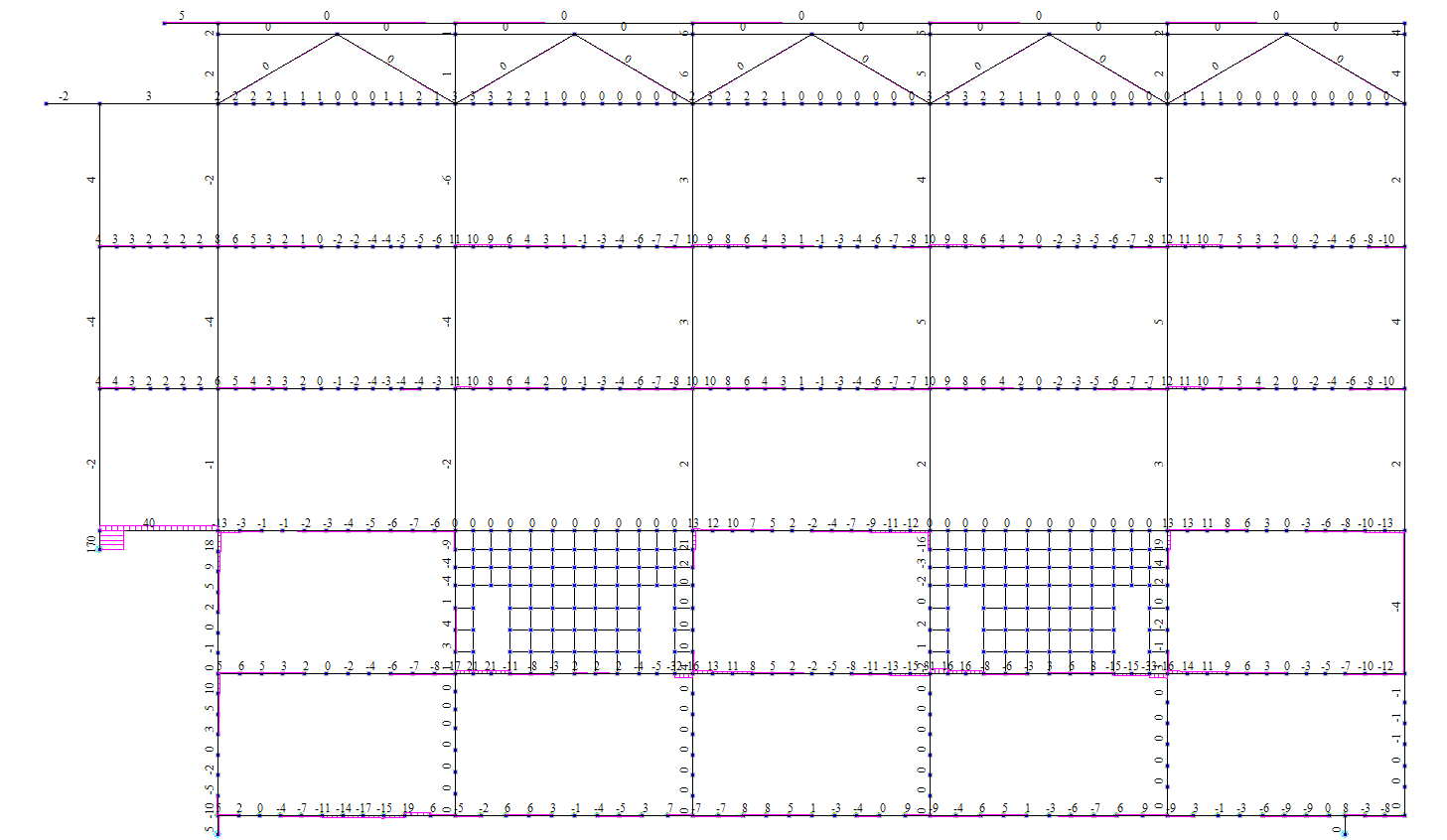
Рисунок 4.33 Сейсмика +Х. Ось Б. Эпюры поперечных усилий Q

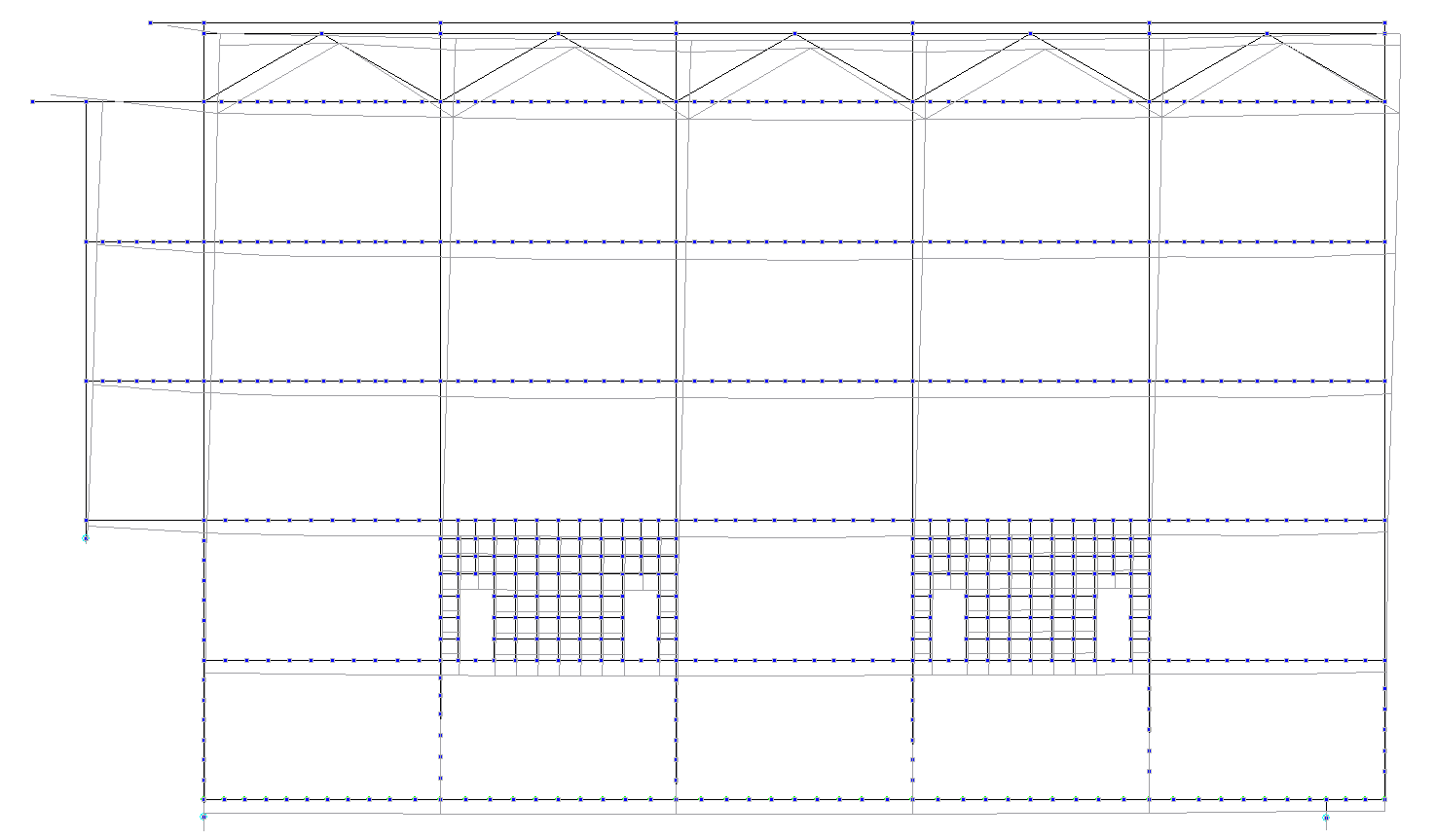
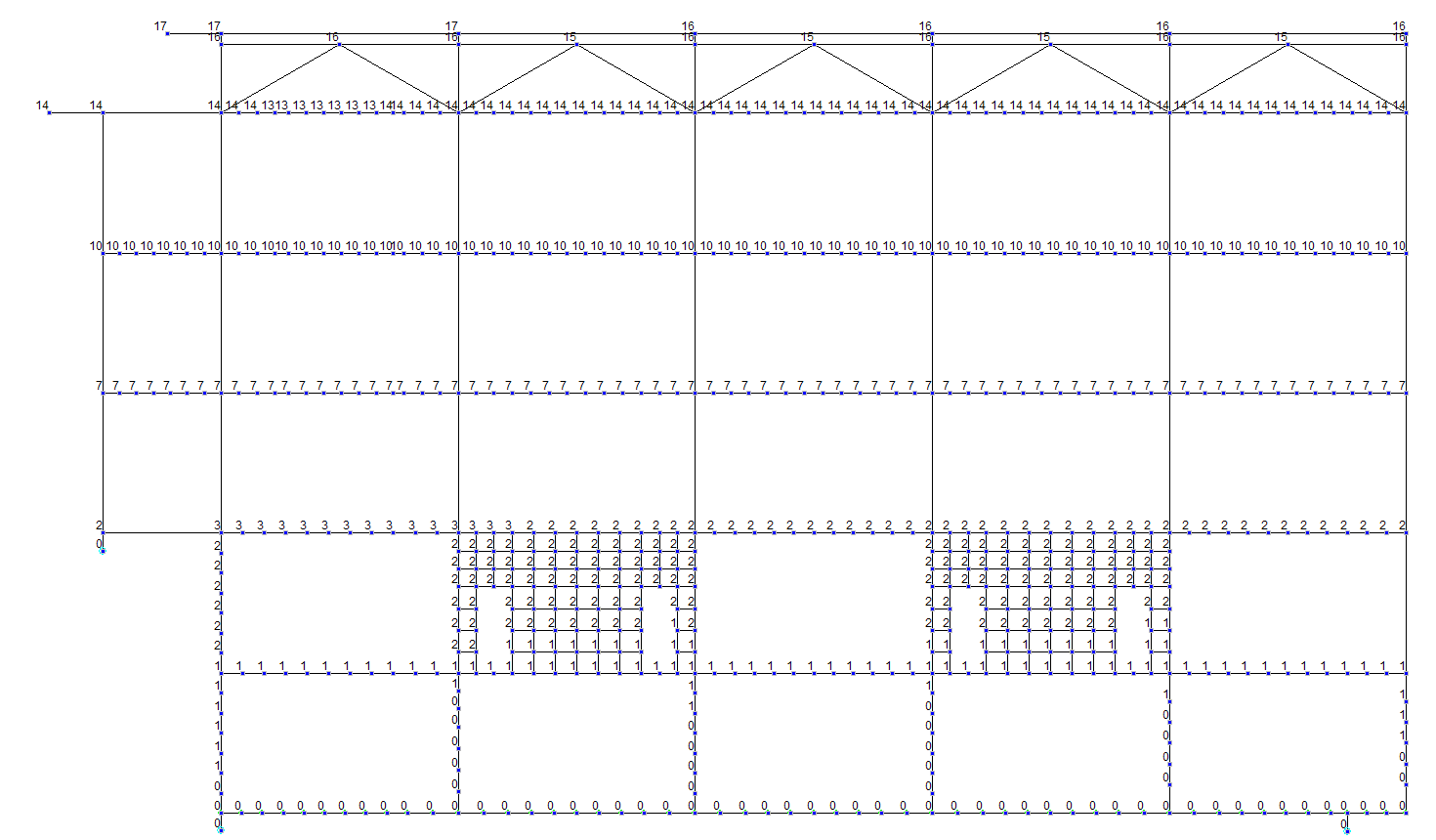
Рисунок 4.34 Сейсмика +Х. Ось Б. Деформации Х

4.6 Подбор сечения элементов металлокаркаса

4.6.1 Проверка сечения средней колонны к1(Ось 6/б) первый этаж

Исходные данные:

Геометрические размеры элемента:

- lefx = 975 см;

- lefy = 819 см;

Нагрузка:

- N = 134 тс = 134 / 0,001 = 134000 кгс;

- Mx = 42 тс м = 42 / 0,00001 = 4200000 кгс см;

- My = 5 тс м = 5 / 0,00001 = 500000 кгс см;

- Qy = 11 тс = 11 / 0,001 = 11000 кгс;

Физические характеристики:

- G = 810000 кгс/см2;

- E = 2100000 кгс/см2;

Прочность:

(Вид металла - Фасонный прокат; Сталь и толщина металла - С345 ; Св. 20 до 40 мм):

- Ryn = 3100 кгс/см2;

- Run = 4700 кгс/см2;

- Ry = 3050 кгс/см2;

- Ru = 4600 кгс/см2;

Коэффициенты надежности и условия работы:

- gc = 0,95 ;

- gu = 1,3 ;

Основные характеристики сечений:

(Сечение ветви - из сортамента; Характеристики сечения - Двутавры колонные с параллельными гранями полок по СТО АСЧМ 20-93; 40 К2; Сечение - одноветьевое):

- h = 40 см;

- b = 40 см;

- t = 1,3 см;

- tf = 2,1 см;

- r = 2,2 см;

- A = 218,69 см2;

- m = 171,67165 кг/м;

- Jx = 66623 см4;

- Jy = 22412 см4;

- Wx1 = 3331,2 см3;

- Wx2 = 3331,2 см3;

- Wy1 = 1120,6 см3;

- Wy2 = 1120,6 см3;

- Sx = 1836,3 см3;

- Jt = 273,18 см4;

- afwx = 1,8 ;

- afwy = 0,28 ;

Характеристики сечения ветви:

- hb = 40 см;

- bb = 40 см;

- tb = 1,3 см;

- tfb = 2,1 см;

- r = 2,2 см;

- Ab = 218,69 см2;

- m = 171,7 кг/м;

- Jxb = 66623 см4;

- Jyb = 22412 см4;

- Wx1b = 3331,2 см3;

- Wx2b = 3331,2 см3;

- Wy1b = 1120,6 см3;

- Wy2b = 1120,6 см3;

- Sxb = 1836,3 см3;

- Jtb = 273,18 см4;

- afwxb = 1,8 ;

- afwyb = 0,28 ;

Характеристики сечения сварного соединения:

- x = 20 см;

- y = 19,9997 см;

Результаты расчета:

1) Расчет на прочность внецентренно-сжатых или внецетренно-растянутых элементов

Проверка условий выполнения расчета по формуле ( 49 ):

Т.к. Ry r 5400 кгс/см2 :

Непосредственне воздействие на элемент динамических нагрузок - отсутствует.

Ослабления стенки отверстиями - отсутствуют.

An = A =218,69 см2 .

t = Qy Sx/(Jx t)=11000 · 1836,3/(66623 · 1,3) = 233,22161 кгс/см2 (формула (29); п. 5.12 ).

2) Продолжение расчета по п. 5.25

Т.к. t/Rs=233,2216/1769=0,13184 r 0,5 и N/(An Ry)=134000/(218,69 · 3050)=0,2009 > 0,1 :

Следовательно расчет должен быть выполнен по формуле ( 49 )

3) Коэффициенты для расчета на прочность элементов стальных конструкций с учетом развития пластических деформаций

Тип сечения по табл. 66 СНиП II - 23-85 - 1.

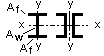
По табл. 66 cx = 1,046 .

По табл. 66 cy = 1,47 .

По табл. 66 n = 1,5 .

Wxnmin = min(Wxn1 ; Wxn2)=min(3331,2;3331,2) = 3331,2 см3 .

Wynmin = min(Wyn1 ; Wyn2)=min(1120,6;1120,6) = 1120,6 см3 .

Изгиб - в двух главных плоскостях.

(N/(An Ry gc))n +Mx/(cx Wxnmin Ry gc)+My/(cy Wynmin Ry gc)=(134000/(218,69 · 3050 · 0,95))1,5+4200000/(1,046 · 3331,2 · 3050 · 0,95)+500000/(1,47 · 1120,6 · 3050 · 0,95)=0,618 r 1 (61,80036% от предельного значения) - условие выполнено (формула (49); п. 5.25 ).

4) Расчет на устойчивость сплошностенчатых стержней при сжатии и изгибе в двух направлениях (Jx>Jy)

Jx=66623 см4 t Jy=22412 см4 (297,26486% от предельного значения) - условие выполнено .

ix = ; Jx/A =; 66623/218,69= 17,45411 см .

lx = lefx/ix=975/17,45411 = 55,86077 .

iy = ; Jy/A =; 22412/218,69= 10,12339 см .

ly = lefy/iy=819/10,12339 = 80,90175 .

ly = ly ; Ry/E =80,90175 · ; 3050/2100000= 3,08318 .

По табл. 72 в зависимости от ly и Ry

fy = 0,61447 .

Wcx = min(Wx1 ; Wx2)=min(3331,2;3331,2) = 3331,2 см3 .

Wcy = min(Wy1 ; Wy2)=min(1120,6;1120,6) = 1120,6 см3 .

mx = (Mx/N) (A/Wcx)=(4200000/134000) · (218,69/3331,2) = 2,05766 .

my = (My/N) (A/Wcy)=(500000/134000) · (218,69/1120,6) = 0,72819 .

l = ly =3,08318 .

m = my =0,72819 .

Т.к. my r 20 :

5) Коэффициент влияния формы сечения

Тип сечения по табл. 73 СНиП II - 23-85 - 5.

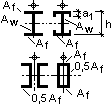
По табл. 73 h = 1,5021 .

6) Продолжение расчета по п. 5.34

mef, y = h my =1,5021 · 0,72819 = 1,09381 .

mef = mef, y =1,09381 .

Т.к. mef, y r 20 :

По табл. 74 в зависимости от ly и mef, y

fey = 0,40574 .

7) Определение коэффициента с для расчета на устойчивость из плоскости изгиба по формуле (56) п. 5.31

Wc = min(Wx1 ; Wx2)=min(3331,2;3331,2) = 3331,2 см3 .

mx = (Mx/N) (A/Wc)=(4200000/134000) · (218,69/3331,2) = 2,05766 .

Тип сечения - открытые.

Т.к. mx r 5; mx > 1 :

a = 0,65+0,05 mx =0,65+0,05 · 2,05766 = 0,75288 .

lc = 3,14 ; E/Ry =3,14 · ; 2100000/3050= 82,39282 .

Т.к. ly=80,90175 r lc=82,39282 :

b=1 .

c = b/(1+a mx )=1/(1+0,75288 · 2,05766) = 0,39228 (формула (57); п. 5.31 ).

Коэффициент с не должен превышать cmax, определяемого в зависимости от коэффициентов:

r = (Jx+Jy)/(A h2)=(66623+22412)/(218,69 · 402) = 0,25446 .

m = 2+0,156 Jt/(A h2) ly2=2+0,156 · 273,18/(218,69 · 402) · 80,901752 = 2,79715 .

d = 4 r/m=4 · 0,25446/2,79715 = 0,36388 .

cmax = 2/(1+d+; (1-d)2+(16/m) (Mx/(N h))2 ) =

=2/(1+0,36388+; (1-0,36388)2+(16/2,79715) · (4200000/(134000 · 40))2 ) = 0,59827 (формула (60); п. 5.31 ).

8) Продолжение расчета по п. 5.34

fexy = fey (0,6 c (1/3)+0,4 c (1/4)) =

=0,40574 · (0,6 · 0,39228 (1/3)+0,4 · 0,39228 (1/4)) = 0,30665 .

N/(fexy A)=134000/(0,30665 · 218,69)=1998,17216 кгс/см2 r Ry gc=3050 · 0,95=2897,5 кгс/см2 (68,96194% от предельного значения) - условие выполнено (формула (62); п. 5.34 ).

Т.к. mef, y=1,09381 < mx =2,05766 :

требуется расчет по формулам (51) и (56), принимая ey=0

lef = lefx =975 см .

9) Расчет на устойчивость внецентренно-сжатых элементов в плоскости действия момента

Тип сечения - спошностенчатый стержень.

10) Определение гибкости стержня

i = ; Jx/A =; 66623/218,69= 17,45411 см .

lx = lefx/i=975/17,45411 = 55,86077 .

l = lefx/i ; Ry/E =975/17,45411 · ; 3050/2100000= 2,12886 .

11) Продолжение расчета по п. 5.27

Wc = min(Wx1 ; Wx2)=min(3331,2;3331,2) = 3331,2 см3 .

m = (Mx/N) (A/Wc)=(4200000/134000) · (218,69/3331,2) = 2,05766 .

12) Коэффициент влияния формы сечения

По табл. 73 h = 1,52638 .

13) Продолжение расчета по п. 5.27

mef = h m =1,52638 · 2,05766 = 3,14077 (формула (52); п. 5.27 ).

Т.к. mef r 20 :

По табл. 74 в зависимости от l и mef

fe = 0,29991 .

N/(fe A)=134000/(0,29991 · 218,69)=2043,0779 кгс/см2 r Ry gc=3050 · 0,95=2897,5 кгс/см2 (70,51175% от предельного значения) - условие выполнено (формула (51); п. 5.27 ).

a = N/(fe A Ry gc)=134000/(0,29991 · 218,69 · 3050 · 0,95) = 0,70512 .

l = lx =55,86077 .

14) Проверка по условию предельной гибкости сжатых элементов

По таблице 19 СНиП II-23-81:

Тип элемента - 4. Основные колонны.

l=55,86077 r 180-60 a =180-60 · 0,70512=137,6928 (40,56913% от предельного значения) - условие выполнено .

15) Продолжение расчета по п. 5.34

Принимаем гибкость для проверки предельной гибкости при изгибе относительно оси x-x:

l = lx =55,86077 .

16) Проверка по условию предельной гибкости сжатых элементов

По таблице 19 СНиП II-23-81:

l=55,86077 r 180-60 a =180-60 · 0,70512=137,6928 (40,56913% от предельного значения) - условие выполнено .

17) Расчет на устойчивость внецентренно-сжатых элементов постоянного сечения из плоскости действия момента при изгибе в плоскости наибольшей жесткости, совпадающей с плоскостью симметрии (Jx>Jy)

Т.к. Jx=66623 см4 t Jy=22412 см4 :

iy = ; Jy/A =; 22412/218,69= 10,12339 см .

ly = lefy/iy=819/10,12339 = 80,90175 .

По табл. 72 в зависимости от ly и Ry

fy = 0,61447 .

18) Определение коэффициента с для расчета на устойчивость из плоскости изгиба по формуле (56) п. 5.31

Wc = min(Wx1 ; Wx2)=min(3331,2;3331,2) = 3331,2 см3 .

mx = (Mx/N) (A/Wc)=(4200000/134000) · (218,69/3331,2) = 2,05766 .

Т.к. mx r 5; mx > 1 :

a = 0,65+0,05 mx =0,65+0,05 · 2,05766 = 0,75288 .

lc = 3,14 ; E/Ry =3,14 · ; 2100000/3050= 82,39282 .

Т.к. ly=80,90175 r lc=82,39282 :

b=1 .

c = b/(1+a mx )=1/(1+0,75288 · 2,05766) = 0,39228 (формула (57); п. 5.31 ).

Коэффициент с не должен превышать cmax, определяемого в зависимости от коэффициентов:

r = (Jx+Jy)/(A h2)=(66623+22412)/(218,69 · 402) = 0,25446 .

m = 2+0,156 Jt/(A h2) ly2=2+0,156 · 273,18/(218,69 · 402) · 80,901752 = 2,79715 .

d = 4 r/m=4 · 0,25446/2,79715 = 0,36388 .

cmax = 2/(1+d+; (1-d)2+(16/m) (Mx/(N h))2 ) =

=2/(1+0,36388+; (1-0,36388)2+(16/2,79715) · (4200000/(134000 · 40))2 ) = 0,59827 (формула (60); п. 5.31 ).

19) Продолжение расчета по 5.30

N/(c fy A)=134000/(0,39228 · 0,61447 · 218,69)=2542,02035 кгс/см2 r Ry gc=3050 · 0,95=2897,5 кгс/см2 (87,7315% от предельного значения) - условие выполнено (формула (56); 5.30 ).

a = N/(fy A Ry gc)=134000/(0,61447 · 218,69 · 3050 · 0,95) = 0,34415 .

Принимаем гибкость для проверки предельной гибкости:

l = ly =80,90175 .

20) Проверка по условию предельной гибкости сжатых элементов

По таблице 19 СНиП II-23-81:

Т.к. a < 0,5 :

a =0,5 .

l=80,90175 r 180-60 a =180-60 · 0,5=150 (53,9345% от предельного значения) - условие выполнено.