2.2 Расчет цилиндрической закрытой косозубой передачи

2.2.1 Выбор материала шестерни и зубчатого колеса:

а) шестерня:

• материал - сталь 45 (У)

• твердость – HB₁ = 240

• σ_в1 = 735 МПа

• σ_Т1 = 431 МПа

б) зубчатое колесо:

• материал - сталь 45 (Н)

• твердость – HB₂ = 200

• σ_в2 = 587 МПа

• σ_Т2 = 333 МПа

Условие выбора материала: HB₁ = HB₂ + (20 ÷ 40)

240 = 200 +40

2.2.2 Расчет допускаемых контактных напряжений:

Принимаем коэффициент ширины зубчатого венца

Определяем коэффициент

- коэффициент безопасности, для нормализованных и улучшенных сталей ;

- коэффициент долговечности [2, c 132].

;

циклов – базовое число циклов;

- эквивалентное число циклов;

- расчетный срок службы передачи.

Для HB₁₍₂₎ ≤ 350 и способе термообработки – улучшение:

σ_{Н lim1(2)} = 2·HB₁₍₂₎ +70

σ_{Н lim1} = 2 ·240+70 = 550 МПа

σ_{Н lim2} = 2 ·200 +70 = 470 МПа

Таким образом:

σ_Н1 = 0,95 ·550 ·1,01 /1,1 = 480 МПа

σ_Н2 = 0,95 ·470 ·1,01 /1,1 = 410 МПа

Тогда расчетные допускаемые контактные напряжения для цилиндрических косозубых колес с небольшой разницей их твердости:

σ_НР = σ_Н1(2)min

Итак, [σ_Н] ]= σ_Н2 = 410 МПа

Межосевое расстояние

Примем по ГОСТ 2185-66 a_w=125

2.2.4 Ширины венцов:

а) зубчатого колеса, мм b₂ = ψ_bа · a_w ;

б) шестерни, мм b₁ = b₂ + (3 ÷ 5)

Здесь ψ_bа – коэффициент ширины шестерни относительно межосевого расстояния.

Тогда b₂ = 0,4 ·125 = 50 мм

b₁ = 50 + 5 = 55 мм

2.2.5 Модуль зацепления:

m-(0.01…0.02)

Полученное значение m ^' округляем до ближайшей величины в соответствии с ГОСТ 9563 – 60:

m_n ≈ m ^'

m_n = 2 мм

Примем предварительно угол наклона зубьев

2.2.6 Суммарное число зубьев передачи:

Z _Σ^' = 2 ·a_w · cos β ^' / m_n

Z _Σ^' = 2 ·125 cos10º / 2 = 123,1

Округляем полученную величину до ближайшего целого числа: Z _Σ^' = 123

2.2.7 Действительный угол наклона зуба:

cos β = Z _Σ · m_n / 2 ·a_w

cos β = 123·2/ 2 ·125 = 0,984

β = arccos 0,984 =10,26 β = 10º 1'

2.2.8 Число зубьев шестерни:

Z₁ = Z_Σ /(u + 1)

Z₁ = 123/(3,1+1)= 30

2.2.9 Число зубьев зубчатого колеса:

Z₂ = Z_Σ −Z₁

Z₂ = 123 – 30= 93

2.2.10 Действительное передаточное отношение:

2.2.11 Диаметры зубчатых колес:

а) начальные диаметры

б) вершины зубьев

2.2.12 Проверка расчетных контактных напряжений:

1) Окружная сила в зацеплении:

2) Окружная скорость колес:

3) Степень точности:

степень точности = f ( , β) ([2], 50, табл.4.2.8) для β >0º и до 17 м/с – передача с повышенными скоростями и повышенными нагрузками – не ниже 7 (точная)

4) Удельная окружная динамическая сила:

, где

- коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля на динамическую нагрузку; = f (HB, β)

Для HB₁₍₂₎ ≤ 350 и косых зубьев = 0,02

- коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса; = f (степень точности,m)

Для m ≤ 10 и степени точности=7 = 5,3

Тогда

5) Удельная расчетная окружная сила в зоне ее наибольшей концентрации:

Здесь - коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; по графику ([2],50, рис.4.2.2) = 1,04

Итак,

6) Коэффициент, учитывающий динамическую нагрузку в зацеплении:

7) Удельная расчетная окружная сила:

,

где - коэффициент внешней динамической нагрузки; из ([2], 51, табл.4.2.9) принимаем = 1,0

Тогда

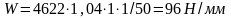
8) Расчетные контактные напряжения:

, где

- коэффициент, учитывающий форму сопряженных поверхностей зубьев; для косых зубьев ,

тогда ;

- коэффициент, учитывающий механические свойства материалов колес, ;

- коэффициент, учитывающий суммарную длину контактных линий; для косых зубьев , где - коэффициент торцевого перекрытия;

Тогда

Итак, расчетные контактные напряжения:

Очевидно, расчетные контактные напряжения меньше допускаемых. Прочность обеспечена.

Допускаемое максимальное контактное напряжение для зубьев:

МПа

МПа

Так как кратковременная перегрузка больше номинальной в 2.5 раза (см. график нагрузки) то расчетное максимальное контактное напряжение:

МПа <

Значит при кратковременной перегрузке зубья по контактной выносливости вполне прочные

Произведем проверочный расчет зубьев шестерни на изгиб. Материал шестерни и колеса одинаков, но толщины зубьев шестерни у основания меньше, чем у колеса, поэтому расчет зубьев на изгиб выполняем для зубьев шестерни.

Эквивалентное число зубьев шестерни

Этому числу зубьев на графике соответствует коэффициент формы зубьев ; (стр.189 [1]).

; при HB=240 ;

Предел изгибной выносливости зубьев МПа (табл.12.7[1])

Допускаемое напряжение на изгиб для зубьев шестерни

МПа

Расчетное напряжение на изгиб

МПа < МПа

Следовательно, на изгиб зубья вполне прочные.

Проверим зубья на пластическую деформацию или хрупкий излом при изгибе при действии на зубья кратковременной перегрузки.

Допускаемое максимальное напряжение на изгиб ( МПа).

МПа

Так как кратковременная перегрузка передачи больше номинальной в 2 раза, то получим

МПа < МПа

Следовательно, и при кратковременной перегрузке зубья на изгиб вполне прочные.

Определяем размеры зубьев.

Коэффициент высоты головки зубьев h_a^*=2;

Коэффициент радиального зазора c^*=0.25;

Высота головок зубьев