12. Қарапайым дифференциалдық теңдеуі (қдт) үшін Коши есебін сандақ әдістерімен шешу. Эйлер әдісі. Эйлердің модификациялық әдісі. Қателіктері.

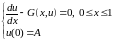, (1)

есебін қарастырайық. 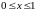кесіндісінде 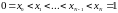, нүктелер жиынын (торды) алайық. 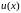шешімі мәндерінің жуық 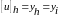шешімінің айырымдылық схемасын жоғарыда алынған торда құрайық:

Бұл схеманың аппроксимация (жуықтау) реті (жуықтау дәлдігі) 1-ге тең. Егер 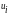есептелсе, онда

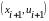нүктесін нүктесіне Oxu жазықтығында 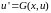дифференциалдық теңдеуінің , нүктесінен өтетін, интегралдық қисығына жанама бойымен жылжытуы.

Осы айтылған әдіс - Эйлер әдісі деп аталады.

Егер функциясы 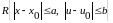тікбұрышта Липшиц шартын қанағаттандырса, 986172 яғни -тұрақты шама және теңсіздігі орындалса, М-тұрақты шама, онда шешімінің қателігінің бағасы төмендегідей болады

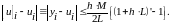
Эйлер әдісін итерация әдісімен жалғастыру.

Енді итерациялық процесс құрамыз

Мысал: . Мұндағы . Есептің дәл шешімі . Эйлер әдісі.

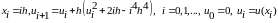
13,14 ҚДТ-нің төрт үшін Рунге-Кутта әдісі. Дәлдігі.

Айталық u_i –дің жуық мәндері x_i нүктелерінде есептелген(белгілі) болсын. Енді u_i+1 мәндерін x_i+1 = x_i +h мәндерінде есептеу керек. Ол үшін бүтін l санын алып, келесі өрнектерді есептейміз:

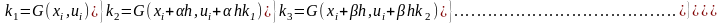(1)

Осыдан кейін

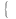
L_h u_h = 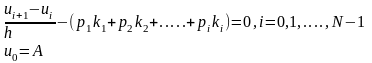(2)

α,β,…,γ және p₁ ,p₂ , …, p_l коэффициенттерін берілген l ушін аппроксимация реті соғұрлым жоғары болатындай етіп таңдаймыз. Егер u_i -ді білсек, онда k₁ ,k₂ ,…,k_l коэффициенттерін есептей аламыз. Сонан кейін

U_i+1 =u_i +h(p₁ k₁ + …+ p_i k_i) (3 )

Эйлер схемасы Рунге-Кутт схемасынан l=1 болғанда алынады.

Теорема 1.

мұндағы

k₁=G(x_i,u_i), k₂=G(x_i+h/2,u_i+k₁h/2), k₃=G(x_i+h/2,u_i+k₂h/2), k₄=G(x_i+h,u_i+k₃h), Рунге-Кутт схемасының аппроксимация реті төртке тең, яғни дәлдігі О(h⁴).

Теорема 2.

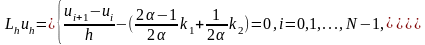(4)

мұндағы k₁=G(x_i,u_i), k₂=G(x_i+ h,u_i+ hk₁), Рунге-Кутт схемасының аппроксимация реті кез келген тұрақты үшін екіге тең, яғни дәлдігі О(h²).

Дәлелдеуі. u’=G(x,u(x)) теңдеуінің шешімі u(x) келесі тепе-теңдікті қанаттандырады 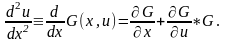Тейлор формуласынан алатынымыз 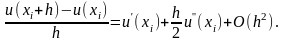Ендеше жоғары тепе-теңдікті пайдалансақ , онда u(x) шешімі келесі теңдікті қанағаттандырады

(5)

Енді, екі айнымалыға тәуелді функциясын h бойынша Тейлор қатарына жіктеп және бірінші дәрежелі мүшелерін ғана қалдырсақ, алатынымыз

(6)

(5) мен (6) –ті салыстырсақ, онда олардың бір-бірімен O(h²) дәлдігімен сәйкес келетінін көреміз. Бұдан шығатыны, u₀ =А дәл берілгендіктен, соңғы өрнектің дәлдігі h бойынша екіге тең. Теорема 2 толық дәлелденді.

Рунге-Кутт әдісімен u_i+1 мәнін есептеу үшін , белгілі u_i бойынша, G(x,u) функциясының мәнін l рет есептеу қажет. Бірақ-та бұл мәндері қайтып қолданылмайды.

15. ҚДТ-нің Адамс және Милн әдістері. Дәлдіктері.

Адамс схемасы

Адамс схемасында әлбір келесі u_i+1 мәнін есептеу үшін, аппроксимация ретіне байланыссыз, G(x,u) функциясының мәні тек қана бір нүктеде есептеу жеткілікті.

Ақырлы айырымдар.Ақырлы айырымдар фурмуласы: ΔG=G_i-G_i-1, Δ²G_i=Δ(ΔG_i)=ΔG_i-ΔG_i-1=G_i-2G_i-1+G_i-2; Δ³G_i=Δ(Δ²G_i)=G_i-3G_i-1+3G_i-2-G_i-3, тағы осы сияқты есептеледі. G_i≡G(x_i,u_i) деп белгілейік. Егер де u_i, u_i-1… белгілі болса, Онда Адамс схемасы бойынша u_i+1-ді есептейтін бірнеше айырымдылық теңдеулерін келтірейік

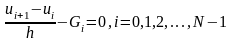дәлдігі O(h) (7)

дәлдігі O(h²) (8)

дәлдігі O(h³) (9)

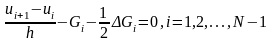дәлдігі O(h⁴) (10)

Мұндағы (7) – Эйлердің айырымдылық формуласы (7)-(10) фурмулалардағы сол жағындағы u_i+1,u_i,u_i-1,… мәндерінің орнына u(x) функциясының дәл мәндерін u((i+1)h, u(h), u(i-1)h),…. Қойсақ, онда (7)-(10) теңдіктерінің үйлесімсіздігі сәйкесінше h, h²,h³,h⁴ болады.

Тапсырма 1. Адамс формуласынан бастап, келесі айырымдылық Адамс формулаларымен жарғастырып жазыңыз. 2. (7)-(10) Адамс формулаларының дәлдігін дәлелдеңіз.

(7) схемасын есептеу үшін u₀=A мәнін білген жеткілікті ал (8) схемасымен есептеу үшін u₀=A мәнінен басқа тағы да алдын ала u₁ мәнін білу керек. Ал (9)-шы схемасы u₀, u₁ және u₂ –лерді білуді талап етеді, т.с.с.

(10) схемасы келесі төрт мәндерін u₀, u₁, u₂, u₃ білуді керек етеді. Осы мәндерін басқа бір әдіспен мысалы Рунге-Кутт әдісімен табуға болады.

Адамс әдістерінің Рунге-Кутт әдісіне қарағанда артықшылығы: бір қадамға аз есептеу керек; ал – кемшілігі : бастапқы есептеулерінің ыңғайсыздығы және есептеу барысында қадам h-ты өзгерте алмауымызда. Ең қолайлысы осы екі әдістерді – Рунге-Кутт пен Адамс кезекпен қолдану.