10. Сандық интегралдау. Ньютон – Котес формуласы. Трапеция, Симпсон және Гаусс фомулалары. Қателіктерінің бағалары.

Есептің қойылымы. интегралын жуықтап есептеу керек.

Алдымен, [a,b] аралығын қадамымен бірдей қашықтықта жататын нүктелерімен n бөлікке бөлеміз және болсын. Енді функциясын (бір-бірінен бірдей қашықтықта жататын түйіндерімен ) Лагранж интерполяциялық полиномымен ауыстырып, келесі жцықтау квадратуралық формуласын аламыз:

(1)

мұндағы -кейбір тұрақты коэффициенттер.

(1)формуладағы коэффициенттерін анықтайық. Ол үшін, түйіндер ара қашықтықтары бірдей болатын, Лагранж интерполяциялық полиномында 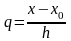жаңа белгілеуін енгіземіз. Сонда алатынымыз:

(2)

мұндағы жалпыланған дәреже.

Енді (1) формулада у функциясын полиномымен ауысырып, (2) өрнекті пайдалансақ, алатынымыз: немесе екенін ескерсек, онда .

болғандықтан , мұндағы - Котес коэффициенттері . (3)

Ендеше , мұндағы , .

Трапеция формуласы, қателігі

(3) формуладан n=1 болғанда алатынымыз

. Ендеше, (5)

(5) формуланың қалдық мүшесі (қателігі) Енді болсын десек, алатынымыз:

Симпсон формуласы және оның қателігі

(3) формуладан n=2 болғанда алатынымыз:

Сондықтан, болғандықтан, алатынымыз - Симпсон формуласы.

қисығы үш нүктелерінен өтетін параболамен ауыстырамыз. Қалдық мүшесі келесі формуламен анықталады

.

11.Нормаланған кеңістіктің аппроксимациясы. Сыртқы және ішкі аппроксимациялары. Үйлесімсіздік, аппроксимация қателігі. Тұрақтылық және жинақтылық.

Нормаланған векторлық кеңістігі W-нің ішкі аппроксимациясы дегеніміз , үштік жиыны: мұндағы

1. - нормаланған векторлық кеңістігі;

2. - - тан W -ге көшіретін сызықты үзіліссіз оператор;

3. - W -ден - ге көшіретін (сызықты болмауы да мүмкін) оператор.

элементі мен элементін салыстырудың ең дұрыс жолы - - пен u-ды W -да немесе -ды -та салыстыру.

_{Екінші жағынан,} u мен u_h - ты салыстыру дегеніміз: u элементінің кейбір бейнесі -ды u_h элементінің кейбір бейнесі

_{Пен басқа бір F кеңістігінде салыстыру. Бұл салыстыру W кеңістігінің сыртқы аппроксимациясы деген ұғымға келеді. Бұл жағдайда ішкі аппроксимация сыртқы аппроксимацияның дербес жағдайы болып қалады.}

_{W нормаланған кеңістігінің сыртқы аппроксимациясы ол келесі жұп:}

_{1.F нормаланған кеңістігі және W кеңістігінен F кеңістігіне}

изоформизмі

2. , үштік жиыны

Мұнда әрбір h үшін нормаланған векторлық кеңістігі;

- - тан F -ке көшіретін сызықты үзіліссіз бейнелеуі;

- W -ден - ге көшіретін (сызықты болмауы да мүмкін) бейнелеуі;

Егер және -тепетеңдік (өзіне өзін) бейнелеуі болса, онда біз, әрине, W кеңістігінің ішкі аппроксимациясын аламыз. Көбінесе, ақырлы кеңісік, -инъективті оператор.

операторы жалғастыру, ал операторы жіңішкерту операторлары деп аталады. Егер W мен F Гильберт операторлары болсв, онда барлық операторлары Гильбертті болады да, аппроксимация Гильбертті аппроксимация деп аталады.

Барлық берілген , , үшін:

1. - мен арасындағы үйлесімсіздік дейміз.

2. - мен арасындағы дискретті үйлесімсіздік дейміз.

3. - -дің аппроксимация қателігі дейміз.