Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казахский национальный университет им. аль-Фараби

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

6. Есептеу математикасына кіріспе-3,4,6,7,8-жок...docx

Скачиваний:

Добавлен:

01.07.2025

Размер:

612.77 Кб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

6. Есептеу математикасына кіріспе

Сызықты алгебралық теңдеулер жүйесін (САТЖ) шешудің нақты әдістері. Бас элементтері Гаусс әдісі. Халецкий әдісі.
САТЖ шешудің итерациялық әдістері. Итерациялық әдістің жалпы схемасы. Релаксация принципі. Қателік және үйлесімсіздік векторлары. Қателік функциясы (функционалы). Итерация процесі жинақталуының қажетті және жеткілікті шарттары. Зейдель әдісі.
САТЖ шешудің оптимизациялық әдістері. Минималды үйлесімсіздік және ең жылдам түсу әдістері.
Алгебралық және трансценденттік теңдеулерді итерациалық әдіспен шешу. Сығып бейнелеу принципі.
Ньютон (жанамалар) әдісі. Қиушылар (хордалар) әдісі. Аралас әдісі.
Ньютон – Канторович әдісі.
Функцияларды интерполяциялау. Ньютонның бірінші және екінші интерполяциялық формулалары, қателіктері.
Функцияларды интерполяциялау. Гаустың бірінші және екінші интерполяциялық формулалары, қателіктері.
Функцияларды интерполяциялау. Лагранж интерполяциялық формуласы, қателігі.
Сандық интегралдау. Ньютон – Котес формуласы. Трапеция, Симпсон және Гаусс фомулалары. Қателіктерінің бағалары.
Нормаланған кеңістіктің аппроксимациясы. Сыртқы және ішкі аппроксимациялары. Үйлесімсіздік, аппроксимация қателігі. Тұрақтылық және жинақтылық.
Қарапайым дифференциалдық теңдеуі (ҚДТ) үшін Коши есебін сандақ әдістерімен шешу. Эйлер әдісі. Эйлердің модификациялық әдісі. Қателіктері.
ҚДТ-нің 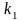және үшін Рунге-Кутта әдісі. Дәлдігі.
ҚДТ-нің төрт үшін Рунге-Кутта әдісі. Дәлдігі.
ҚДТ-нің Адамс және Милн әдістері. Дәлдіктері.
Екінші ретті ҚДТ үшін шекаралық есептерін шешудің сандық әдістері. Ақырлы айырымдар әдісі. Қуалау әдісі және оның орнықтылығы мен жинақтылығы. Қателігі.
Екінші ретті ҚДТ үшін шекаралық есептерін шешудің оптимизациялық сандық әдістері. Галеркин әдісі. Ең аз квадраттар әдісі. Коллокация әдісі.
Жылуөткізгіштік теңдеуінің сандық әдістері. Айқындалған, айқындалмаған және Кранк – Николсон әдістері. Қателіктері.
Тербеліс теңдеуінің сандық әдістері. Салмақтары бар сандық әдістері.
Пуассон теңдеуіне қойылған Дирихле айырымдылық есебінің сандық әдістері. Қалаптастыру әдісі. Айқындалған, айқындалмаған және айнымалы бағыттар схемалары.

1.Сызықты алгебралық теңдеулер жүйесін (сатж) шешудің нақты әдістері. Бас элементтері Гаусс әдісі. Халецкий әдісі.

САТЖ шешу әдістерін негізгі екі топқа бөлуге болады: 1. Дәл әдістері- жүйе шешімін есептердің есептеудің ақырлы алгоритмдерін береді (Камер, Гаусс, негізгі элементтер, квадрат түбірлер т.б. әдістер). 2. Итерациялық әдістер – берілген дәлдікпен жинақталатын шесіз процесстер арқылы жүйе шешімін алуға мүмкіндік береді (итерация, Зейдель, релаксация т.б. әдістері).

Дөңгелектеу нәтижесінде дәл әдістердің де нәтижелері жуық болуы мүмкін, оның үстіне, жалпы жағдайда, түбір қателігінің бағасын алу қиындық тудырады. Ал итерациялық процесстерді қолданғанда тағы әдіс қателігі қосылады. Итерациялық әдістерді тиімді пайдалану бастапқы жуықтауды таңдауға және процесс жинақтылығының тездігіне байланысты екенін байқаймыз. Гаусс әдісі. Белгісіздерді жою алгоритмі.

(1)

(негізгі элемент) болсын. (1) жүйенің бірінші теңдеуінің коэффициенттерін -ге бөліп, алатынымыз:

Мұндағы,

(2) теңдеуін қолданып, (1) жүйеден ді жоюға болады. Бұл үшін (1) жүйенің екінші теңдеуінен ге көбейтілген (2)теңдеуді , (1) жүйенің үшінші теңдеуінен ге көбейтілген (2) теңдеуді, т.с.с. алып тастаймыз. Нәтижесінде үш теңдеуден тұратын жүйе аламыз:

( )

Мұндағы (i,j 2) коэффициенттері (i,j 2) формуласымен анықталады.

(2)жүйенің бірінші теңдеуінің коэффициенттерін - негізгі элементке бөліп, келесі теңдеуді аламыз:

( )

Мұндағы (j>2).

Енді -ні -ді жойғандағыдай жойып, келесі теңдеулер жүйесіне келеміз:

( )

Мұндағы (i,j>2).

(4) жүйенің бірінші теңдеуінің коэффициенттерін - негізгі элементке бөліп, аламыз:

( )

Мұндағы (j>3).

-ті жоғарғыдағыдай (4) жүйеден жойып, алатынымыз:

( )

Мұндағы (i,j 4).

Бұдан

( )

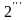Қалған белгісіздер , және теңдеулерден біртіндеп анықталады.

Сонымен, сызықты жүйені Гаусс әдісімен шешу процессі үшбұрышты матрицалы , , , эквивалентті жүйені құруға әкеледі. Әдісті қолданудың қажетті және жеткілікті шартты барлық «негізгі элементтерінің» нөлден өзгешелігі.

Халецкий әдісі

(1)

Матрицасын үшбұрышты матрица мен диаганалі бірлерден тұратын жоғарғы үшбүрышты матрицасын көбейтіндісі ретінде қарастыруға болады, яғни

(2)

Мұндағы

Онда және элементтері келесі формулалармен анықталады:

(3)

(4)

Бұдан ізделінді векторын

(5)

Теңдеулерді біртіндеп шешу арқылы табуға болады. В және С матрицалары үшбұрышты болғандықтан, 5 жүйелері оғай шешіледі, яғни

(6)

(7)

(6) формуласынан белгісіздері коэффициенттерімен бірге есептеген ыңғайлы көрінеді.

Егер А- симметриалы болса, яғни онда

2.САТЖ шешудің итерациялық әдістері. Итерациялық әдістің жалпы схемасы. Релаксация принципі. Қателік және үйлесімсіздік векторлары. Қателік функциясы (функционалы). Итерация процесі жинақталуының қажетті және жеткілікті шарттары. Зейдель әдісі.

САТЖ шешудің итерациялық әдістері. Итерациялық әдістің жалпы схемасы.

Ax=b , 1)

A= , x= , b= , ,

Жүйенің бірінші теңдеуін -ге қатысты , екіншісін және т.с.с шешейік. Нәтижесінде келесі эквивалент жүйесін аламыз.

мұндағы , , , ( және 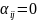егер i=j .

, (2 )жүйесін мына түрде жазайық

жүйесін біртіндеп жуықтау әдісімен шешеміз. Нөлдік жуықтау ретінде аламыз. Ары қарай (бірінші жуықтау)

(екінші жуықтау) және т.с.с.

(3)

, болса онда бұл шек (2) жүйенің шешімі болып табылады. Шынында да , (3) теңдеуінде шекке көшсек: немесе яғни х- шектік элемент шешімі болып табылады. Онда ол (1) жүйенің де шешімі. (3) теңдеулерін ашып жазсақ:

деп алу керек , мұндағы Онда (1) жүйеден + мұндағы , (3) және ( ) итерация әдісі деп аталады.

Итерация процесі жақсы жинақталады , яғни (1) бір жүйе түбірлерін берілген дәлдікпен алу үшін жуықтау саны көп болмайды , егер

матрицасының элементтері абсолют шамасы бойынша өте аз болса . Басқаша айтқанда , итерация әдісін тиімді қолдану үшін (1) жүйенің диагональ элементтерінің модульдері осы жүйенің диагональ емес коэфиценттерінің модульдерімен салыстырғанда өте үлкен болу керек.

Жинақталатын итерация процесі өзін өзі түзету қасиетіне ие , яғни есептеулердің кейбір қателіктері соңғы нәтижеге ықпалын тигізбейді, онда қате жуықтауды жаңа бастапқы вектор деп қарастыруға болады.

Кейбір жағдайда жуықтауды есептегеннен олардың айырмасын есептеген ыңғайлы. Белгілеулерді еңгізіп , (k=0,1,…) (3) формуладан алатынымыз: (4)

(5)

теңдікті алсақ (6)

(7)

деп қабылдасақ , онда m-інші жуықтау (8)

егер болған жағдайда да орындалады. Керісінше , (8) өрнек k=0 болған жағдайда орындалмайды.

k=1,2,… және , онда табатынымыз :

Итерация процесі жинақтылығының жеткілікті шарты

Теорема: (1) келтірілген сызықты жүйе үшін итерация процесі оны жалғыз шешіміне жинақталады , егер матрицасының қандай да бір канондық нормасы бірден кіші болса , яғни итерациялық процесс ( ) үшін жинақтылықты жеткілікті шарты:

Сызықтық теңдеулер жүйесі үшін итерация процесі жинақтылығының қажетті және жеткілікті шарты

Теорема: Кез-келген бастапқы вектор мен кез келген бос мүшесі үшін келесі итерация процесінің

Жинақталуы матрицасының меншікті мәндері , яғни характеристикалы теңдеуінің 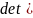𝜆E)=0 барлық түбірлері модулі бойынша бірден кіші болуы қажетті және жеткілікті. (айталық , ) болсын , яғни - матрицасының спектральды радиусы болсын . Онда 2 итерациялық процесінің жинақталуының қажетті және жеткілікті шарты -

Зейдель әдісі

Зейдель әдісі қарапайым итерация әдісіне қарағанда жақсы жинақтылықты береді. Бірақ та өте көп есептеулерді қажет етеді. Қарапайым итерация әдісі жинақталмаған жағдайда Зейдель әдісі жинақталуы мүмкін. Зейдель әдісі қарапайым итерация әдісінен жайыр жинақталатын кездері болады.

Теорема1: Егер

сызықты жүйе үшін