Толқындық қозғалыстың сипаттамалары

Толқын ұзындығы

Бірдей фазада тербелетін іргелес екі нүктенің ара қашықтығы толқын ұзындығы деп аталады.

Толқынның таралу жылдамдығы

,

, онда

Толқынның таралу жылдамдығы заттың туріне және оның күйіне тәуелді, жиілік пен толқын ұзындығына тәуелсіз.

Толқын энергиясы

Барлық толқындардың, табиғатына байланыссыз, ең негізгі қасиеті – олардың затты тасымалдамай, энергияны тасымалдау.

Тасымалданған энергияның сапалық сипаттамасы – толқынның энергия ағынының тағыздық векторы немесе толқын интенсивтігі немесе Умов векторы.

Умов векторының белгіленуі:

, мұнда - энергияның көлемдік тығыздығы

- толқын таралатын ортаның тығыздығы

- циклдік жиілік

- орта бөлшектерінің тербеліс жиілігі

- толқының жылдамдығы

Үлкен масштабты толқындар (инерциялық толқындар немесе Росби толқындары) –синоптикалық маңызды толқындар. Олардың ұзындықтары бірнеше тәулікте мыңдаған км-ге жетеді. Тербелістің амплитудасы қысым өрісінде-10гПа (гектопасаль), ал желдің өрісінде- 10м/c. Егер толқындар үлкен масштабты процестердің бөлігі болса, онда олардың жорамалдық модельдерді жасағанда ескерілетіні анық.

Үлкен масштабты немесе макромасштабты процесстер 1мыңнан-10мың км-ге дейін созылатын горизонтал масштабтармен сипатталады. Олар 1-10 тәулік аралығында жетіледі. Ондай процестерге циклогенез, сорғалап ағатын (струйные) ағыстар және т.б. жатады

12. .

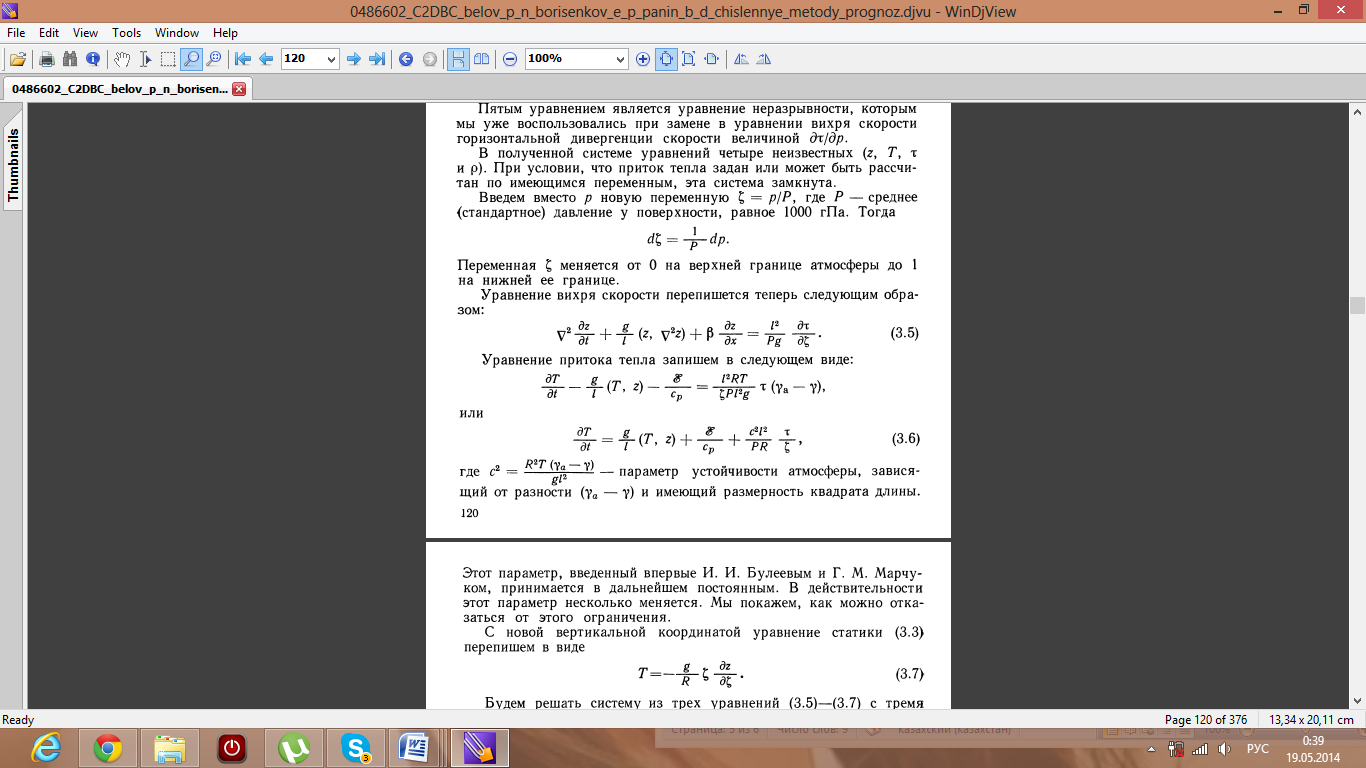
Уравнения квазигеострофических прогностических моделей

можно получить исходя из системы полных уравнений гидротер-

модинамики крупномасштабных атмосферных процессов. Для

бароклинной атмосферы в изобарической системе координат эти

уравнения имеют вид

— параметр статической устойчивости; Fx и Fy — компоненты

силы турбулентной вязкости, отнесенной к единице массы; & —

приток тепла к единице объема.

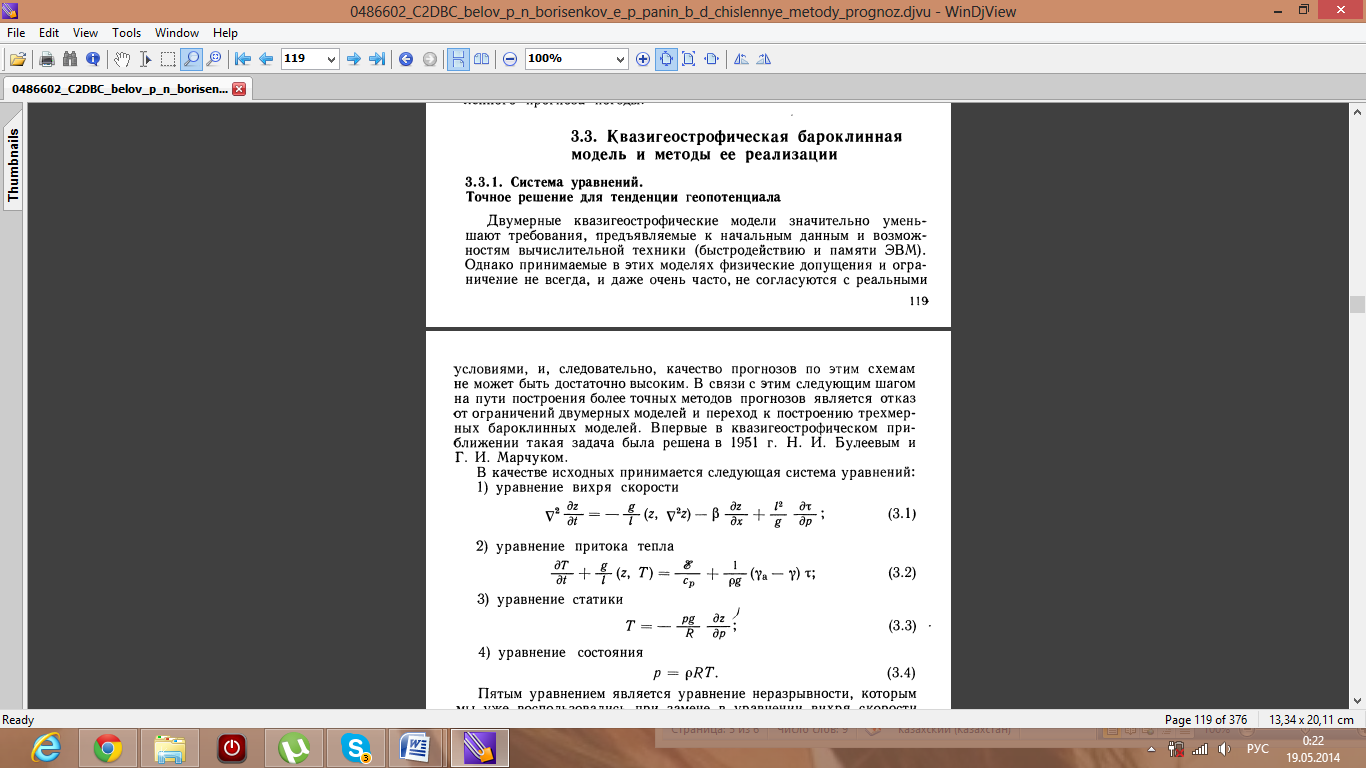
В качестве условий на верхней и нижней границах атмосферы

принимаются:

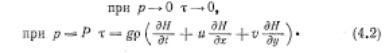
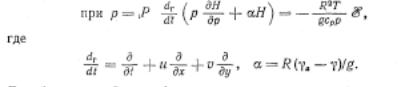
Для баротропной атмосферы полные уравнения имеют вид

Используя метод разложения по малому параметру е = 1 !l0t0

(параметру И. А. Кибеля), можно показать, что между проек-

циями скорости и высотой изобарической поверхности существуют

соотношения

Уравнения прогностических квазигеострофических моделей

атмосферы получаются на основе систем полных уравнений гидро-

термодинамики (4.1) или гидродинамики (4.3) при использовании

соотношений (4.4). Однако наиболее целесообразный путь пре-

образований уравнений заключается в следующем. Прежде всего

с помощью уравнений движения выводится уравнение вихря ско-

рости, которое после исключения несущественных членов имеет

вид

— горизонтальная дивергенция скорости.

В баротропной варианте далее из полученного уравнения вихря

скорости исключается горизонтальная дивергенция с помощью

третьего уравнения системы (4.3). Наконец, в полученном урав-

нении компоненты скорости заменяются их геострофическими

значениями.

В бароклинном варианте горизонтальная дивергенция скорости

исключается с помощью уравнения неразрывности. Далее с по-

мощью уравнения притока тепла исключается аналог вертикаль-

ной скорости т, а затем с помощью уравнения статики исключается

температура. В результате после замены компонент скорости и

и о их геострофическими значениями получается одно уравнение

для Я.

При учете в прогностических моделях неадиабатических фак-

торов необходим расчет величины притока тепла входящей

в уравнение притока тепла системы уравнений (4.1). Остановимся

здесь на методике расчета части притока тепла, обусловленной

переносом лучистой энергии &л. Лучистый приток тепла к единице

объема выражается через радиационный баланс