7.Жарнамалық компанияның моделі. Жарнамалық компаниялардың алғашқы этаптарының ерекшеліктерін көрсету және рычагтың жарнаманың тиімділігіне әсері.

Дифференциалдық теңдеулер экономикада әр түрлі динамикалық процестерді жазуда қолданылады. q(t) жарнамалық өсімді көрсетеді,ол жарнамалық бюджеттің расходымен анықталады,мысалға теңгемен,компанияның бір апталық жарнамаға кеткен ақшасы.

• Величина A(t) описывает осведомленность целевой группы потенциальных покупателей нового товара или услуги.

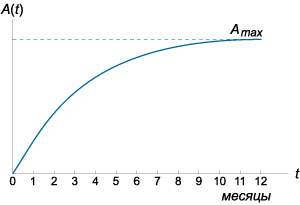
Мұңдағы b- жарнаманың эффективтілігін көрсететін тұрақтылық, к –константа.

Алнған теңдеу сызықты дифференциалдық бірінші ретті теңдеу болып табылады.Оны мына түрде жазған ыңғайлы:

Бұдан шығатыны дифференциалдық теңдеудің шешімі мына формуламен көрсетіледі

С интегралы бастапқы шарттан табылады A(t₀) = A₀. 

8. Жер асты қайықтың жету мәресіне дейінгі уақытын және жүзіп өту ұзақтығын анықтау. Жүзіп өту процесінің моделін құру кезінде қандай жорамалдар қолданылды.

Алдымен Ньютонның 2-ші заңын векторлық турде жазайық.

F cnp + Fapx+ mg =ma (1)

Мұндағы F cnp –судың кедергісі, Fapx Архимед күші, m – қайықтың массасы,a-қайықтың үдеуі.

F cnp x = ma x , (2)

F _{cnp y} + F _apxy - mg _y = ma _y (3)

Fapx=P ж Vл g – итеруші күш (Архимед), F cnp= - kv кедергі күші,мұндағы v қайықтың жылдамдығы ал к кедергі коэффециенті.

(2) және (3) теңдеулерден келесі дифференциалдық теңдеуді аламыз. (4)

(5)

Бастапқы шарттарды пайдалана отырып теңдеуді шешеміз.У роекций осінің бастапқы жылдамдығы 0, ал Х осінікі V_x , Х және У проекцияларының бастапқы координаталары Х₀ және У₀ .

9. Қандай заң жер асты судың гравитациялық ағысының моделінің негізіне жатады

Жер асты судың гравитациялық моделі мына теңдеу бойынша анықталады.

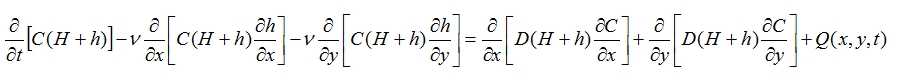
– С(х,t) – искомая концентрация примесей;

– Q(х,у,t) – известная интенсивность источника загрязнения;

– v = мрg – коэффициент, определяемый свойствами грунта;

– р – плотность жидкости;

– g – ускорение свободного падения;

– D – коэффициент гидродинамической дисперсии (аналог коэффициента теплопроводности в законе Фурье);

– Н, h – const.

Бұл теңдеуді бастапқы және шекаралық шарттарды қолдану арқылы шешеміз:

U_t-ΔU=|sin t|U_t=0 = 0

∇U*h+U=0

Для свободной области: ( Бос облысқа)

∂U/∂t=0

U_t=0=0

U|_∂Ω=0

Бұл шарттар бізге гидравликалық барьер береді ол барьер бізге жер асты суларын ласанып кетуден сақтап тұрады.

11. Атмосферадағы толқынды қозғалыстар туралы негізгі түсінік. Толқынды қозғалыстың математикалық анализі үшін шағын ауытқу әдісі. Үлкен масштабты толқындар.

Егер тербеліс таралатын материалдық орта бөлшектерінің тербеліс бағыты толқынның таралу бағытымен бағыттас болса, ондай толқындарды қума толқындар деп атайды.

Тербеліс бағыты Толқынның таралу

бағыты

Егер материалдық орта бөлшектерінің тербелісі толқынның таралу бағытына перпендикуляр бағытталған болса, ондай толқындарды көлденең толқындар деп атайды. Тербеліс бағыты

Толқынның таралу

бағыты