Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казахский национальный университет им. аль-Фараби

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5. Математикалық пішіндеуге кіріспе-10,13-25-жо...docx

Скачиваний:

Добавлен:

01.07.2025

Размер:

1.15 Mб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

5. Математикалық пішіндеуге кіріспе

1. Математикалық моделдерді құрудың негізгі қағидалары және олардың

ерекшеліктері. Қағидалардың біреуін пайдаланып серіппедегі салмақтың

тербелісінің математикалық моделін құру.

2. Сатурн сақинасына дәлдік дененің тартылу күшін анықтау. Оның Бүкіл

әлемдік тартылыс күшінен ерекшелігі.

3. Ішек тербелісінің кинетикалық және потенциалдық энергиясы.Ішек

тербелісіне варияциялық әдіспен модель құру.

4. Циалковский формуласы. Заманауи ғарыштық зымыранның корпусының

конструкциясын таңдаудағы иерархиясын көрсету және түсіндіру.

5. Сызықтық және сызықтық емес модельдердің айырмасы және

ерекшеліктері.Сызықтық модельден сызықтық емес модельге өтуге

мысалдар келтіру.

6. Мемлекеттік эканомиканың өсуінің жүйелік теңдеуі.Модельдердің

тұйықталу қажеттілігі.

7. Жарнамалық компанияның моделі. Жарнамалық компаниялардың

алғашқы этаптарының ерекшеліктерін көрсету және рычагтың

жарнаманың тиімділігіне әсері.

8. Жер асты қайықтың жету мәресіне дейінгі уақытын және жүзіп өту

ұзақтығын анықтау. Жүзіп өту процесінің моделін құру кезінде қандай

жорамалдар қолданылды.

9. Қандай заң жер асты судың гравитациялық ағысының моделінің негізіне жатады.

10. Жер асты судың ағысының иерархиялық моделін көрсету.Ол қалай қорытылады.

11. Атмосферадағы толқынды қозғалыстар туралы негізгі түсінік. Толқынды қозғалыстың математикалық анализі үшін шағын ауытқу әдісі. Үлкен масштабты толқындар.

12. Атмосфералық қозғалыстарды кiшi параметрге және квазигеострофика бойымен жiктеу.

13. Үлкен масштабты атмосфералық қозғалыстар болжамы туралы есептер қою.

14. Гидродинамика теңдеулерiн жеңiлдету. р- жүйе координатындағы үзіксіздік теңдеуінің тұжырымы.

15. Жергiлiктi мезопроцесс болжамдарының жіктелген (тәптiштелген) есептері. Мезопроцесс модельдері үшiн негiзгi теңдеулер.

16. Атеросклеротикалық түйінді тамырда қан айналымының бастапқы және шекаралық шарттарын келтіріп есеп қойылымын құрыңыз. Негізгі теңдеулерлердің сандық әдіс шешімдерін сипаттаңыз. Тұрақты айырымдылық әдісі.

17. Динамикалық аспектілердің кеңістіктік қан ұюының және тромб өсуін түсіндіріңіз. Феноменологиялық модельді сипаттаңыз.

18. Негізгі метаболиттік ұю жүйесіндегі кинетикалық өндірісті және диструкцияны , олардың ағын ауысуын және таралуын, сипаттайтын математикалық моделін құрыңыз.

19. Популяция көбеюінің ықтималды математикалық моделін сипаттаңыз

20.Популяция түрлерінің бір бірімен әрекеттесу моделін құру кезіндегі негізгі Вольтер гипотезаларын көрсетіңіз.

21. Екі популяция түрлерінің арасындағы бәсекелестік математикалық моделін құру және тұрақты күй жүйесіне баға беріңіз.

22. Экологияның не екенін түсіндіріңіз. Популяция өсуінің шектеулі және шектеусіз математикалық моделін құрыңыз.

23. Инфекциондық аурулардың қарапайым математикалық моделін құрыңыз және тұрақты тепе теңдік күй жүйесіне баға беріңіз.

24. Инфекциондық аурулардың, негізгі параметрлер негізінде, математикалық моделіндегі аурудың шарықтау шегін сипаттаңыз.

25. Микробтық популяциядағы микроорганизмдердің жас ерекшеліктері бойынша бөлінуінің математикалық моделі.

1 Математикалық моделдерді құрудың негізгі қағидалары және олардың ерекшеліктері. Қағидалардың біреуін пайдаланып серіппедегі салмақтың тербелісінің математикалық моделін құру

Табиғаттың фундаменталь заңдары нақты бір жағдайға фундаменталь заңдарды қолданылады. Бірінші планға қандай заңдар қолдану керек және және қалай жасау керек екені шығады.

Заңдар:

А)сақталу заңы .мысалы оқтың жылдамдығын білу үшін жеңіл қатты босс стерженьде айналатын маятник – жүк типін қолдана алады

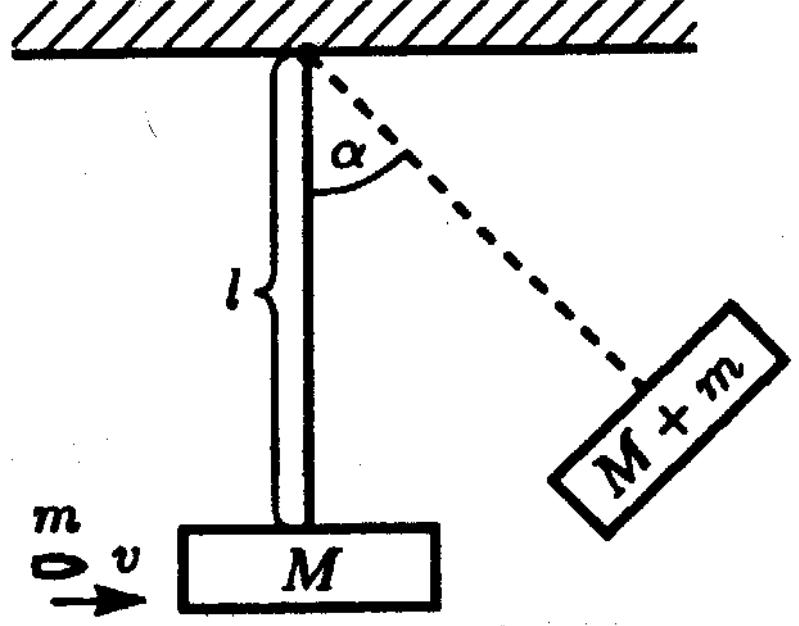
L- стержень ұзынд

g - Еркін түсу үдеуі

-Ең үлкен ауытқу бұрышы

Б) материяның сақталу заңы: мысалы бассейнді толтыру есебін жатқызуға болады, шыққан және құйылған суды есептеу

В) импульстің сақталу заңы:сыртқы күштің әсерінсіз болатын жүйенің толық импульсі сақталады

2 Сатурн сақинасына дәлдік дененің тартылу күшін анықтау. Оның Бүкіл әлемдік тартылыс күшінен ерекшелігі.

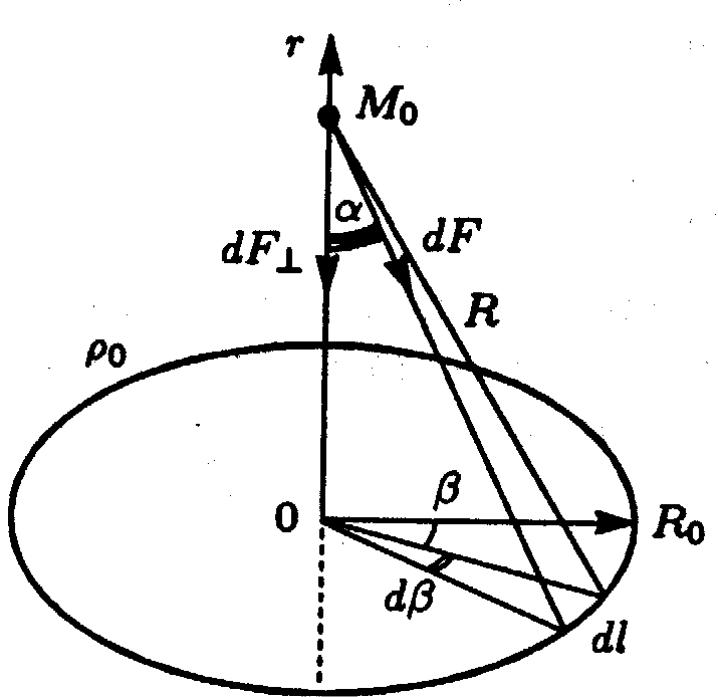
массаның қозғалыс моделін құрайық.

Қозғ сақина осі бойымен жүреді.

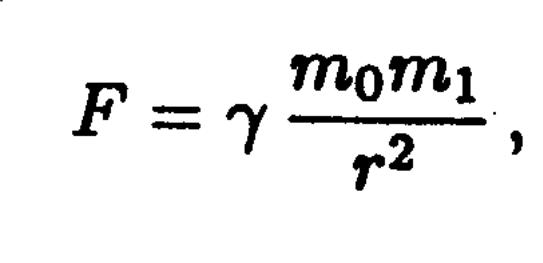
екі дененің массасы, r – екеуінің арақашықтығы , - тартылыс турактысы,

мен dm массалар арасындағы күш

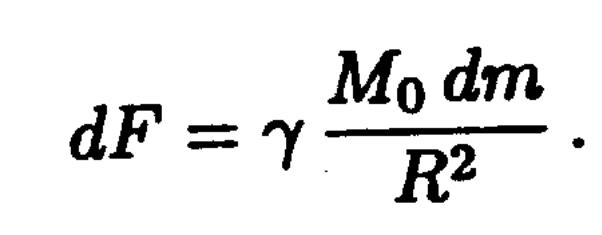
R, r - массаның сақинаға және центрге дейінгі арақашықтығы

болған кездегі.

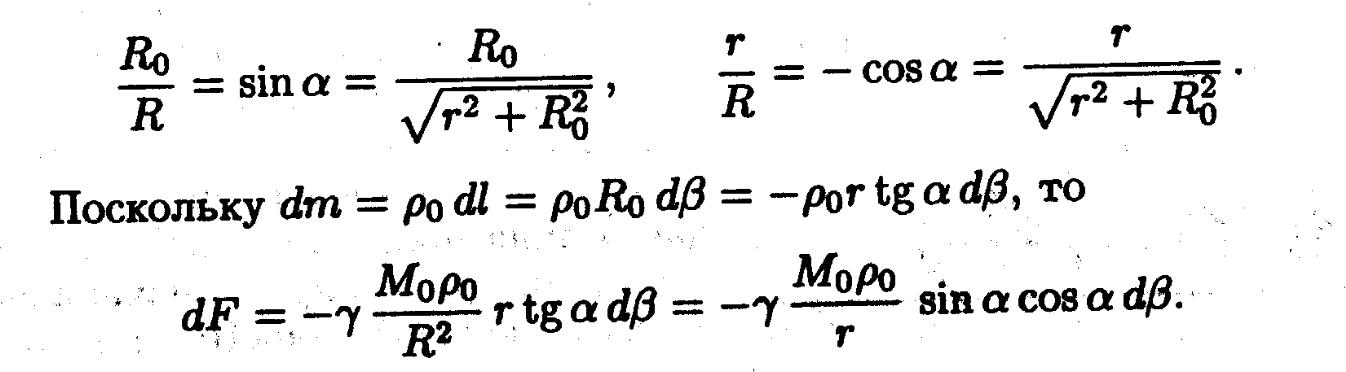
dF күшінің r осіне проекциясын табайық (осы проекция бізге керекті қозғалысты анықтайды):

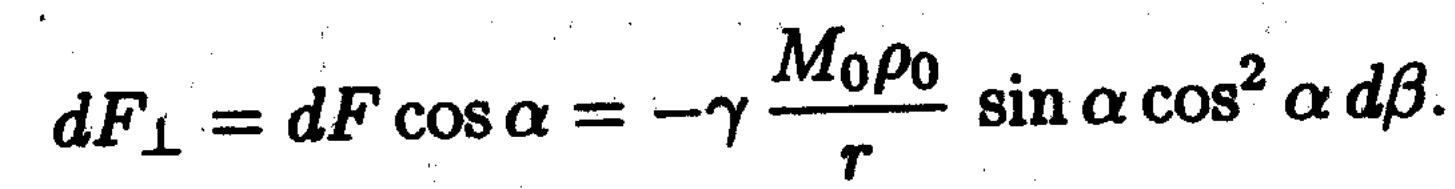
Тартылыс күшерінің қосындысын тауып, яғни - бойынша - тен -ге дейін - тан интеграл тауып қорытқы күшті анықтайық:

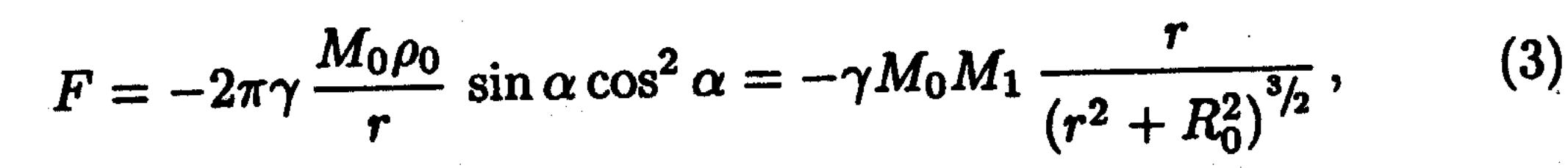
-сақинаның толық массасы

Қорытқы күштің горизонталь проекциясы нольге тең

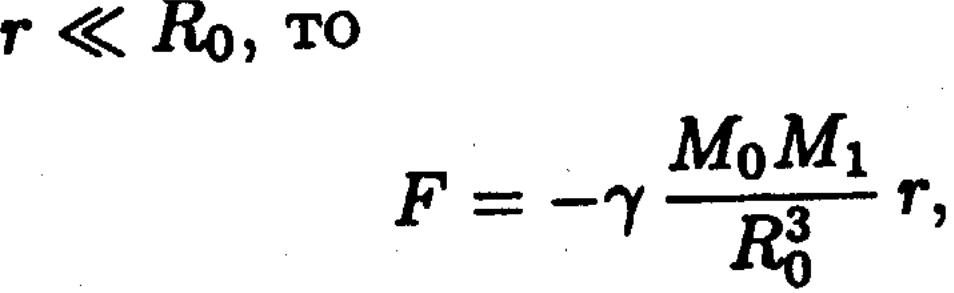
массаға екінші Ньютон заңын қолдансақ r осі боймен қозғалысты анықтаймыз:

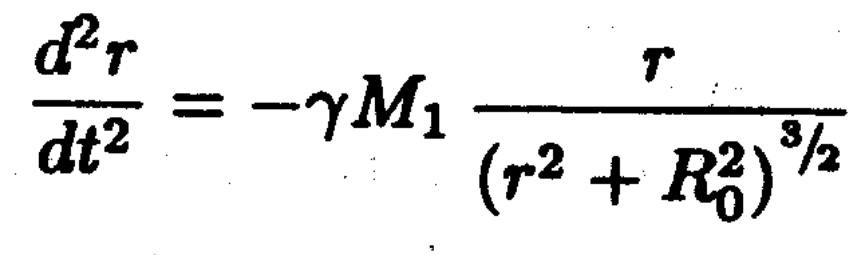
Сызықты емес теңдеу болып табылады және тек болғанда сызықты болады.

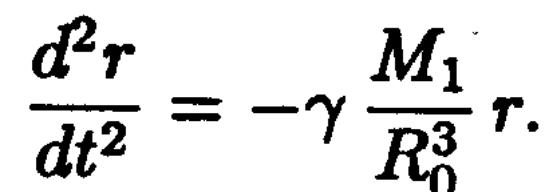
3 Ішек тербелісінің кинетикалық және потенциалдық энергиясы.Ішек

тербелісіне варияциялық әдіспен модель құру.

Күштің әсерінен қозғалатын жағдайды айналып қозғалатын материялық нүктенің механикалық жүйесін қарастырайық. Потенциял энергиясы

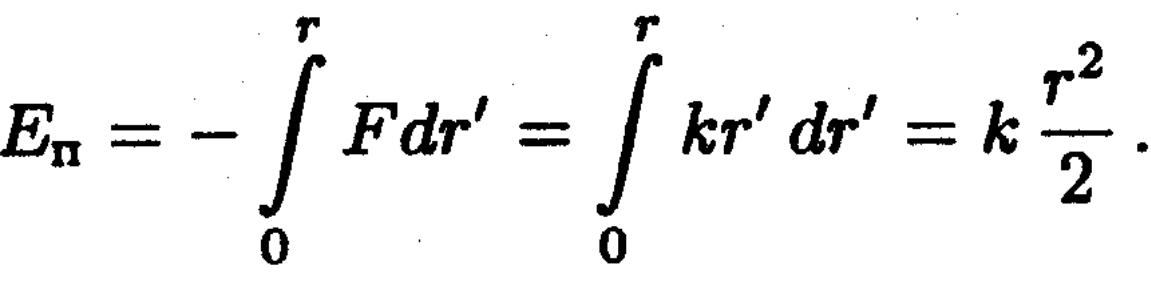
Ал кинетикалық энергиясы

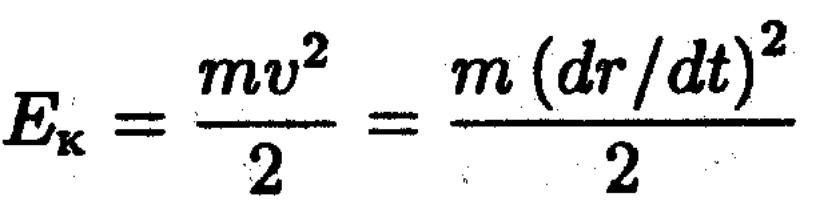
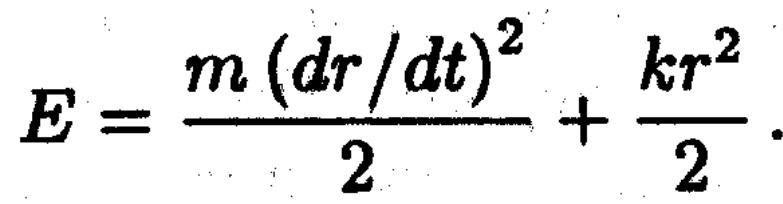
варияциялық әдіспен модель құру.:

шарик жылдамдыгы

Лагранж формуласы

Енди варияциядағы r(t) координатаның әрекетін есептейік:

деп:

4. Циалковский формуласы. Заманауи ғарыштық зымыранның корпусының конструкциясын таңдаудағы иерархиясын көрсету және түсіндіру

Циолковский формуласы, ракетаның ұшу траекториясының активті телімінің соңғы бөлігінде (яғни қозғалтқыш жұмысының аяқталу кезеңінде) ауырлық күші, аэродинамикалық күш және басқа да сыртқы күштер әсер етпеген кездегі ракетаның шекті (ең үлкен) жылдамдығын анықтайды. Циолковскийдiң формуласы жоқ болғанда барлық басқа күштер ракета қозғаушының тартуын әсермен ұшақты жетiлдiретiн жылдамдық бағыт бойынша өзгерiссiз анықтайды. Бұл жылдамдықтар мiнездемелiк деп аталады.

мұндағы:

V—ұшақтың соңғы жылдамдығы (барлық отынның өндiрулерiнен кейiн)

I — (отынның массасының секундтық шығынына қозғаушының тартуын қатынас) ракета қозғаушының меншiктi импульсi;

— (отынның + аппаратының конструкциясының + пайдалы жүктемесi) ұшақтың бастапқы массасы.

— (конструкцияның + пайдалы жүктемесi) ұшақтың түпкi массасы;

Циолковскийдiң формуласы айнымалы массаның материалдық нүктесi үшiн дифференциалды теңдеудiң интегралдауы Мещера жолымен алына алады:

Мұндағы

m—нүктенiң массасы;V—нүктенiң жылдамдығы;U— оның массасының бөлiгi бөлетiн нүктелер жылжитын салыстырмалы жылдамдық. Бұл шамалардың ракета қозғаушысы үшiн және меншiктi импульс оны құрайды Бұл түтiктiң кесiгi және қоршаған ортада қысымдардың теңдiгiнде әдiлдердiң жылулық ракета қозғаушы үшiн. Дегенмен, Циолковскийдiң формуласы өз әдiлдiгi, бұл шарттың орындалуынан тәуелсiздi сақтайды.