19. Лаплас теңдеуі. Фундаментальды шешім. Гармоникалық және аналитикалық функциялар.
Лаплас теңдеуі
,
Пуассон теңдеуі
,
т.б. теңдеулер.
Біз
эллиптикалық теңдеулердің
кеңістіктердегі есептерімен шұғылданамыз.
-
айнымалы,
- параметрлі нүктелер;
-
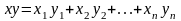және
векторлардың скаляр көбейтіндісі;
-
және
нүктелердің ара қашықтығы деп қабылдаймыз.
Екі
- тұрақтандырылған, ал
- айнымалы нүктлер болса, онда
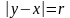центрі
нүктеде радиусы
болған
- сфера, ал
- шар деп айтамыз.
Егер
радиус
болып,
аймақ
шар ішінде, яғни
орында болса, онда
аймақ шенелген деп айтылады.
Бір
байланысты бет (
жағдайда)
аймақты
- ішкі және
- сыртқы, шексіз нүктелерді қамтитын
аймақтарға ажыратады. Шенелген
аймақ шекарасын
(немесе
)
әрпімен белгілейік;
деп сол
бетке сырттай тұрғызылған
- бірлік вектор, мұндағы
-
вектордың бағыттаушы косинустары.
Егер
болып Лаплас теңдеуін
аймақта қанағаттандырса, оны Лаплас
теңдеуінің регулярлық шешімі деп айтады;
оны әдетте гармониялық
функция
дейді. Ал, егер Лаплас теңдеуінің шешімі
функция шексіздік нүкте төңірегінде:
жазықтықта шенелген, ал
кеңістікте
түрінде баяу азайса (
ұмтылғанда), яғни жалпы жағдайда
болса, онда
функцияны шексіздікте регулярлықта
деп айтады.
2. Есептің қойылуы
Лаплас теңдеуіне шекаралық есептердің қойылуларын көрсетейік (басқа эллиптикалық теңдеулерге осылайша, кейбір өзгерістер болуы мүмкін).
А)
Дирихленің ішкі есебі
:
;
б)
Дирихленің сыртқы есебі
:
;
шексіздікте
регулярлы
шешімді анықтау керек.
В)
Нейманның ішкі есебі
:
;
г)
Нейманның сыртқы есебі
:
шексіздікте регуляр шешімін анықтау
керек;
д) Жалпылама (үшінші текті) ішкі және сыртқы есептер:
|
|
регуляр
функцияны анықтау керек.
§2 Лаплас теңдеуінің іргелі шешімдері
Анықтама. Лаплас теңдеуінің тек арақашықтыққа – айнымалы нүктемен параметрлік
нүктеге дейінгі қашықтыққа тәуелді
шешімін оның іргелі немесе элементар
(қарапайым) шешімі деп атайды.
А)
,
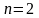яғни
теңдеудің іргелі шешімін анықтайық. Ол
үшін
поляр координаталар жүйесіне өтейік:
.
(1)
Іргелі
шешімінің анықтамасы бойынша (1) теңдеудің
шешімі
- тек ара қашықтыққа тәуелді функция
болуы керек, сондықтан (1) теңдеу
түріндегі
екінші ретті жай дифференциалдық
теңдеуге айналады. Оны екі рет интегралдап
- түріндегі жалпы шешімін аламыз, мұндағы
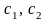- еркін тұрақты шамалар, мәселен
деп алып,
жағдайдағы Лаплас теңдеуінің
(2)
іргелі шешмін анықтаймыз.
Б)
.
Бұл жағдайда
сфералық координаталар жүйесіне өтіп,
одан кейін жоғарыдағыдай іргелі шешім
анықтамасын ескеріп Лаплас теңдеуін
түріндегі екінші ретті жай дифференциалдық теңдеуді аламыз, оны екі рет интегралдап
,
мұндағы еркін тұрақтыларда жоғарыдағыдай
таңдап алып
(3)
жағдайдағы Лаплас теңдеуінің іргелі шешімін анықтаймыз. Алынған (2), (3) – іргелі шешімдерін біріктіріп
(4)
іргелі шешімдерді жазамыз.
Бұл
(4) өрнектен іргелі шешімінің
нүктеден басқа жерлерде гармониялық
функция екендігін көреміз, яғни
.
Оның үстіне (4) өрнектен кеңістікте іргелі шешім регуляр функция, ал - жазықтықта шексіздікте логарифмдік ерекшелікте болады.
Іргелі шешімнің физикалық мағынасын анықтау үшін алдымен іргелі шешім
-
тан
- нормаль вектор бағыты бойынша туындыны
есептейік. Мына
- айнымалы,
- тұрақтандырылған нүктелер деп
алып
,
есептейміз,
бірақ мұндағы
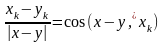болғандықтан
,
демек
мұндағы
-
вектор мен
вектор арасындағы бұрыш. Бұларды
біріктіріп
(5)
егер
вектормен
векторлар
бағыттас болса, онда (5) өрнек
(5’)
түрінде
жазылады, себебі
.
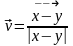Егер бұл өрнектердегі пен нүктелердің мағыналарын кері қабылдасақ, онда
демек,
(6)
орынды.
Ньютон потенциалы. кеңістіктегі тұрақтандырылған нүктеде бірлік оң заряд орналасқан деп алайық. Ол заряд, Кулон заңы бойынша, төңірегінде электр өрісін жасайды. Қолайлы бірлік жүйе таңдап алып, ол өріс күшін
түрінде өрнектеп, ол күш нүктеден нүктеге қарай бағытталған. Бұл күштің вектор бағытына проекциясы
(7)
болады.
Енді осы (7) өрнекпен (5) - іргелі шешімнің
бағыт бойынша туындысын салыстырып,
мынадай қорытындыға келеміз: Лаплас
теңдеуінің
іргелі шешімі деп
нүктеде орналасқан бірлік зарядтың
электр өрісінің электростатистикалық
потенциалы екенін көреміз.