17. Жылуөткізгіштік теңдеуі үшін Грин функциясы әдісі.
Дирихле есебі үшін Грин функциясы. (12.1) – Пуассон теңдеуінің шешімін табуға Гриннің негізгі формуласын қолданып,
(12.1.1)
теңдігін
аламыз. Белгілі
функциясы төмендегі, яғни
1)
нүктесінің координаталарына байланысты
облысында бірінші ретті үзіліссіз
дербес туындылары бар, ал
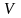облысында гармониялық функция;
2)
- бетінде -
шектік мәнді қабылдайтын функция;
шарттарын қанағаттандыратын болсын.
және
функцияларына Гриннің екінші формуласын
қолданып,
немесе
екендігін ескеріп,
(12.1.2)
теңдігін аламыз. (12.1.1) теңдігінен (12.1.2) теңдігін алу арқылы
(12.1.3)
теңдігіне
келеміз. Осы теңдіктегі
функциясын Пуассон теңдеуіне қойылатын
ішкі Дирихле есебінің Грин
функциясы
деп атайды және оны
деп белгілейді. Сонымен,
18. Жылуөткізгіштік теңдеуі үшін экстремум қағидасы және салдары.
Параболалық типтегі жылу өткізгіш
(1)
теңдеуін
қарастыралық, мұндағы
деп
мезеттегі
нүктедегі жылу (температура),
(
- жылу өткізгіштік коэффициент,
- ішкі сиымдылық,
- тығыздық).
А)
Аралас
есеп:
(1) теңдеуден шекарасы
бет
аймақта
уақытта
(2)
шекаралық және
(3)
бастапқы шарттарды қанағаттандыратын -температураны анықтау керек.
Б)
Коши
есебі:
- жолақта (1) теңдеудің (3) бастапқы шартты
- шексіз аймақта (сан осі, шексіз жазықтық
немесе үш өлшемді шексіз кеңістік)
қанағаттандыратын шенелген шешімін
анықтау керек.
Егер
жағдайды қарастыру үшін
нүктедегі
(4)
-
жұп (немесе
),
-тақ (немесе
)
болуына байланысты
функцияны
- жарты өске жұп - тақ жалғастырып қарау
керек.
Максимум қағидасы
Аралас есептегі шешімнің жалғыздығы мен берілген шамаларға тәуелділік мәселелерін тексеру және Коши есебінің шешімінің жалғыздығын дәлелдеу максимум қағидасына тікелей байланысты.
Мына
аймақта максимум қағидасын келтірейік.
Біртекті
жылу өткізгіштік теңдеудің регулярлық
шешімі тұйық аймақтың барлық нүктелерінде
үзіліссіз болып өзінің ең үлкен және
ең кіші мәндеріне тек аймақтың шекарасы
- да ие, болмаса
моментке ие болады.
Салдар.
Егер жылу өткізгіш теңдеудің регулярлық
және тұйық аймақта үздіксіз
шешімдері ол аймақ шекарасында
теңсіздікті қанағаттандырса, онда бұл
теңсіздіктің
- цилиндрдің барлық нүктелері үшін де
орынды, яғни
.
Тақырыбы: Максимум қағидасының қолдануы
1-теорема.
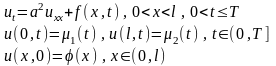(7)
аралас есептің регулярлық және тұйық аймақта үзіліссіз шешімі жалғыз.
2-теорема. Аралас (7) есептің тұйық аймақта үзіліссіз шешімі тиянақты.
Ескерту. Келтірілген екі теореманың тұжырымдары жылу өткізгіш теңдеуі үшін қойылған басқа түрлі аралас есептер үшінде орынды.
3-теорема. Мына Коши есебінің
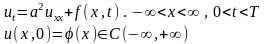(8)
регуляр, шенелген шешімі жалғыз.