13. Жылуөткізгіштік теңдеуі. Коши есебі. Пуассон формуласы.
Шексіз
аймақтағы біртекті жылу өткізгіш
(36)
теңдеуінің
(37)
бастапқы
шарт белгілі болғанда шешімін анықтау
керек. Мұндағы белгілі
- үзіліссіз және шенелген, яғни
үшін
болсын.
Тұрпаттама шешімі
Есептің шешімін Фурье тәсілімен
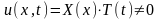(38)
түрінде іздейміз. әзірше тұрпаттама түрде
(41)
өрнектеледі; мұны әдетте Пуассон формуласы (интегралы) деп атайды.
Шешімнің регулярлығы
Енді (41) өрнекті (36) - (37) есептің үзіліссіз регулярлық шешімі екенін дәлелдейік.
Алдымен
(42)
функция (36) теңдеуді қанағаттандыратынын көрсетейік:
Міне бұл екі өрнектен
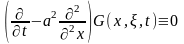
теңбе-теңдігі шығады. Әдетте (42) функцияны жылу өткізгіш теңдеудің іргелі шешімі деп айтады.
Енді (41) өрнектің есептегі (37) бастапқы шартты қанағаттандыратынын көрсетейік. Ол үшін алдымен мына тұжырымды дәлелдеу керек.
Лемма.
Егер
функция
аралықта үзіліссіз және шенелген болса,
онда (41) Пуассон интегралы
мәндерінде шексіз дифференциалданады,
ол туындылар интеграл астында есептелінеді.
Теорема. Егер функция сан өсте үзіліссіз және шенелген болса, онда (41) Пуассон интегралы (36) - (37) есептің регулярлық шешімі болады.
Қорытынды.
Егер
функция
сан өсте үзіліссіз және шенелсе, онда
Пуассон интегралы:
Жылу өткізгіш теңдеуін
қанағаттандырады;Коши шартын қанағаттандырады;
Коши есебінің шешімі (Пуассон интегралы) шексізм интеграл астында дифференциалданады.
Сол интеграл шамасындай жылу өте үлкен жылдамдықпен тарайды.
16. Жылуөткізгіш теңдеу үшін Коши есебін айнымалыға жіктеу–Фурье тәсілімен шешу
Жазықтықта
жан-жағынан бекітілген, қабырғалары
және
болатын тік төртбұрышты мембрана
бастапқы ауытқу мен бастапқы жылдамдық
арқылы тербеліске түсетін болсын.
Мембрананың тепе-теңдік жағдайынан
ауытқуын сипаттайтын U(x,y,t)
функциясын табу үшін
(9.9.1)
тербеліс теңдеуінің
(9.9.2)
бастапқы шарттарын
(9.9.3)
(9.9.4)
шекаралық
шарттарды қанағаттандыратын
класында жататын классикалық шешімін
табу керек.
1-қадам
. (9.9.1) теңдеуінің шешімін
және
функцияларының көбейтіндісі түрінде
іздестіреміз, яғни
.
және
функцияларын табу үшін U(x,y,t)
функциясының дербес туындыларын табып,
(9.9.1) теңдеуіне қойып, айнымалыларын
ажыратып,
функциясы үшін
(9.9.5)
теңдеуін, ал v(x,y) функциясы үшін
(9.9.6)
(9.9.7)
(9.9.8)
шекаралық есебін аламыз.
2 – қадам. (9.9.6) – (9.9.8) есебін Фурье әдісін қолданып шешеміз, яғни шешімін
түрінде
іздестіреміз. Айнымалыларды ажыратып,
және
функцияларына байланысты
(мұндағы
,
шамалары
теңдігімен байланысты тұрақтылар)
меншікті мән туралы бір өлшемді есептерді
аламыз. (9.9.9)-(9.9.10) мен (9.9.11)-(9.9.12) есептерінің
сәйкесінше шешімдері
формулалары арқылы өрнектеледі. Сондықтан (9.9.6)-(9.9.8) есебінің
меншікті мәндеріне
өзіндік
функциялары сәйкес келеді. Мұндағы
- қандай да бір тұрақты көбейткіш. Осы
көбейткішті
функцияларының нормасы
болатындай етіп таңдап аламыз. Бұдан
-
жүйесінің ортогональді жүйе құрайтыны
айқын. Сондықтан
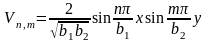(9.9.13)
функциялары (9.9.6)-(9.9.8) тікбұрышты мембрананың ортонормаланған өзіндік функциялар жүйесін құрайды.
3 – қадам. - параметрінің табылған
мәндерін (9.9.5) теңдеуіне қойып, оны шешеміз:
4 – қадам. 2-3 қадамдарының нәтижелерін пайдаланып, (9.9.1) теңдеуінің дербес шешімдерін жазамыз:
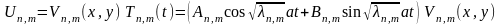
(9.9.1) теңдеуі біртекті және сызықты болғандықтан, оның дербес шешімдерінің сызықтық комбинациясынан тұратын
,
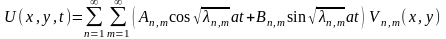(9.9.14)
мұндағы функциясы (9.9.13) формуласымен анықталады, функциясы да оның шешімі болады және ол (9.9.3)-(9.9.4) шекаралық шарттарын қанағаттандырады.
5
– қадам. Бастапқы шарттарды пайдаланып,
(9.9.14) теңдігіндегі
және
коэффициенттерін анықтаймыз. Ол үшін
ең бірінші (9.9.14) қатарын формальді
аргументі бойынша дифференциалдаймыз:
(9.9.15)
(9.9.14) және (9.9.15) қатарларындағы -нің орнына 0 қойып, бастапқы шарттарды ескеріп
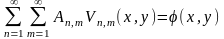(9.9.16)
(9.9.17)
теңдіктерін аламыз.
Фурье
қатарлар теориясынан белгілі (9.9.16),
(9.9.17) қатарлары берілген
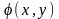және
функцияларын (9.9.6)-(9.9.8) есебінің
өзіндік функциялары арқылы Фурье
қатарына жіктеліп тұрғанын көрсетеді,
онда оған сәйкес келетін Фурье қатарының
коэффициенттерін
,
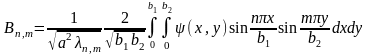
формулалары арқылы табамыз. Осы коэффициенттерді нақты бастапқы және функциялары үшін есептеп және олардың табылған мәндерін (9.9.14) теңдігіне апарып қойып, берілген (9.9.1)-(9.9.4) есебінің шешімін табамыз.
Фурье еселі қатарлар теориясын қолданып (9.9.14) қатарының жинақталатындығын және оны мүшелеп дифференциалдауға болатындығын негіздеуге болады.