12, 14. Біртекті емес теңдеу үшін шекаралық есептерді Фурье әдісімен шешу.

Біртекті емес жылуөткізгіштік теңдеуі үшін қойылатын шекаралық есепті шешу. Біртекті емес жылуөткізгіштік теңдеуіне қойылатын бастапқы – бірінші шекаралық есепті қарастырайық:

(9.3.1)

теңдеуінің

(9.3.2)

шекаралық шарттарды

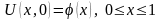(9.3.3)

бастапқы шартын қанағаттандыратын класында жататын классикалық шешімін табу керек.

Әдетте біртекті емес дифференциалдық теңдеуге қойылатын шекаралық есептердің шешімін табу үшін оны шешімдерінің қосындысы берілген есептің шешімін анықтайтындай етіп қосымша есептерге жіктейді. Нақты қандай есептерге жіктеу керектігін анықтау үшін берілген есептің шешімін белгісіз функциялардың қосындысы түрінде іздестіреді. Осы әдісті пайдаланып, (9.3.1)– (9.3.2) есебін қосымша есептерге жіктейік. Ол үшін оның шешімін

(9.3.4)

түрінде іздестіреміз және белгісіз функциялары қандай есептердің шешімі болатындығын анықтау үшін (9.3.4) формуласымен анықталатын функцияны (9.3.1-9.3.3) есебіне апарып қоямыз.

(9.3.5)

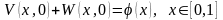(9.3.6)

(9.3.7)

(9.3.5)- (9.3.7) теңдіктерінен функциясын келесі

(9.3.8)

(9.3.9)

(9.3.10)

теңдеу біртекті, бастапқы шарт біртекті емес, шекаралық шарттары біртекті болатын бірінші қосымша есептің шешімі болатындай, ал функциясын келесі

(9.3.11)

(9.3.12)

(9.3.13)

теңдеу біртекті емес, бастапқы және шекаралық шарттары біртекті болатын екінші қосымша есептің шешімі болатындай таңдаймыз. Әрі қарай төмендегідей қадамдар жасаймыз.

1-қадам. (9.3.8)- (9.3.10) бірінші қосымша есептің шешімін табамыз. Бұл есепті 9.2 пунктінде қарастырған болатынбыз. Оның классикалық шешімі 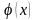функцияның кесіндісінде үзіліссіз бірінші ретті туындысы бар болып, шарттарын қанағаттандырған кезде (9.3.5) формуласы арқылы, яғни

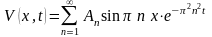(9.3.14)

қатары арқылы анықталады. Мұндағы формуласы арқылы табылады. Сонымен, функциясын таптық.

2-қадам. (9.3.11)- (9.3.13) екінші қосымша есептің шешімін табамыз. Екінші қосымша есептің шешімін

(9.3.15)

түрінде іздестіреміз. Мұндағы – белгісіз табуды қажет ететін функция. (9.3.15) - облысында бірқалыпты жинақталатын және аргументтері бойынша мүшелеп дифференциалдауға болатын қатар деп ұйғарайық. Онда оның қосындысы функциясы (9.3.12) бастапқы шартты қанағаттандыратын болады. (9.3.15) қатарына (9.3.12) бастапқы шартын қойып, функциясы үшін

(9.3.17)

шартын аламыз.

Берілген функциясы кесіндісінде аргументі бойынша Фурье қатарына жіктелетін болсын, яғни

, (9.3.18)

мұндағы

. (9.3.19)

(9.3.15) қатарын (9.3.11) теңдеуіне апарып қойып,

(9.3.20)

теңдігін аламыз. функциясының (9.3.18) және (9.3.20) жіктеулерін салыстыра отырып, жіктеудің жалғыздығын ескеріп,

(9.3.21)

біртекті емес, сызықты коэффициенттері тұрақты бірінші ретті жай дифференциалдық теңдеуіне келеміз.

Сонымен, функциясын анықтау үшін (9.3.21) дифференциалдық теңдеуімен (9.3.17) бастапқы шартын таптық. Бұл – функциясына байланысты Коши есебі. Коши есебін шешу үшін сызықты жай дифференциалдық теңдеулер теориясының нәтижелерін қолданамыз.

(9.3.21) теңдеуінің жалпы шешімін тұрақтыларды вариациялау әдісін пайдаланып құрамыз. Әуелі (9.3.21) теңдеуіне сәйкес келетін біртекті емес теңдеудің жалпы шешімін

(9.3.22)

түрінде іздестіреміз. Мұндағы белгісіз функциясы

теңдігінен анықталады. Бұдан интегралдау арқылы

,

теңдігін аламыз. функциясының мәнін (9.3.22) теңдігіне апарып қойып, (9.3.21) дифференциалдық теңдеуінің

(9.3.23)

жалпы шешімін аламыз. (9.3.23) теңдігінен бастапқы шартты ескеріп, болатындығын көреміз. Сонымен, егер функциясы кесіндісінде үзіліссіз болған кезде Коши есебінің шешімі

(9.3.24)

формуласы арқылы анықталатын болады. Табылған функциясының мәнін (9.3.15) теңдігіне апарып қойып, екінші қосымша есептің

(9.3.25)

формальді шешімін табамыз. Мұндағы функциясы (9.3.15) формуласы арқылы табылады.