10. Толқын теңдеуі үшін шеттік есебінің шешімінің жалғыздығы және функциялар қасиеттері

(1)

теңдеуін толқын теңдеуі, ал бұл теңдеудің шешімін толқын деп атайды. Бұл теңдеу қолданыста жие кездеседі. болған кезде

(2)

теңдеуі кеңістікте таралатын дыбыстың таралу құбылысын сипаттайды.

(1) теңдеуі үшін характеристикалық форма

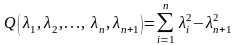(3)

болған кезде (1) теңдеуінің шешімін табуда тұжырымы өте маңызды мына лемманы келтірейік.

Лемма: Егер

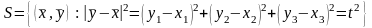
сфера, ал 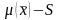сферасында берілген екі рет үзіліссіз дифференциалданатын кез-келген нақты функция болса, онда

(4)

формуласымен анықталатын функция (2) теңдеуінің классикалық шешімі болады.

Дәлелдеуі. Лемманы дәлелдеу үшін

алмастыруын енгізіп, (4) формуласын

(5)

түрінде жазамыз. Мұндағы - бірлік сфера 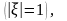ал оның элементар ауданы. (3) формуласынан

(6)

теңдігін аламыз. Сонымен қатар

, (7)

Мұндағы

, (8)

ал сферасының нүктесіне сырттай жүргізілген нормаль вектор.

(7) теңдігін дифференциалдау арқылы

(9)

теңдігіне келеміз.

Тегіс 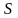шекарасымен шенелген 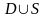тұйық облысында өзінің бірінші ретті туындысымен қоса үзіліссіз нақты функциялары үшін Гаусс-Остроградский формуласы

(10)

орындалатындығы математикалық анализ курсынан белгілі факт. Осы формуланы (8) теңдігінің оң жағына қолданып

(11)

формуласын аламыз. Мұндағы - центрі нүктесіне орналасқан радиусы -ға тең болатын ашық шар, ал - элементар көлем. Кеңістіктегі декарттық координаталары мен 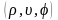сфералық координаталары

байланыстары арқылы берілетіндігін ескеріп, (11) теңдігінен

(12)

теңдігін аламыз.

(9) теңдігін ескеріп,

(13)

теңдігіне келеміз. (6) мен (13) формулаларын салыстырып, біз (4) формуласымен анықталатын функциясының (2) теңдеуінің классикалық шешімі болатынығын көреміз.

Айта кететін жәйт,

өрнегі функциясының сферасы бойынша алынған интегралдық ортасын анықтайды.

11. Біртекті теңдеу үшін шекаралық есептерді Фурье әдісімен шешу. Штурма–Лиувиль есебінің меншікті мәні мен меншікті функциясы, қасиеттері.

Фурье әдісінің жалпы схемасы. Дербес туындылы дифференциалдық теңдеулер үшін қойылатын шекаралық есептерді шешу үшін ең бір көп тараған эффектілі әдістердің бірі – Фурье әдісі. Ол сызықты біртекті шекаралық есептерді шығаруға қолданылады. Бұл әдісті көбінесе басқаша айнымалыларды ажырату немесе өзіндік функциялар әдісі деп те атайды.

Фурье әдісінің негізгі идеясы, дербес туындылы дифференциалдық теңдеу үшін қойылатын шекаралық есептерді жай дифференциалдық теңдеулер үшін қойылатын шекаралық есептерге немесе тәуелсіз айнымалылар саны азырақ болатын дербес туындылы дифференциалдық теңдеуге келтіру. Мысалы, егер теңдеу екі және тәуелсіз айнымалыларын қамтитын болса, онда бұл теңдеудің U(x,t) шешімін жай дифференциалдық теңдеулердің шешімі болатын және функцияларының көбейтіндісі түрінде іздестіріледі. Нәтижесінде осы теңдеудің дербес шешімдері табылады. Сосын осы шешімдердің сызықты комбинациясынан алғашқы шекаралық есептің шешімі құрастырылады.

Енді осы әдісті пайдаланып, кейбір қарапайым шекаралық есептердің шешімін алу жолдарын толық зерттейік.

Жылуөткізгіштік теңдеуі үшін қойылатын шекаралық есепті шешу.

Жылуөткізгіштік теңдеуі үшін қойылатын бастапқы – бірінші шекаралық есепті қарастырайық:

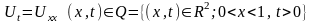(9.2.1)

теңдеуінің

(9.2.2)

шекаралық шарттарды

(9.2.3)

бастапқы шартын қанағаттандыратын класында жататын классикалық шешімін табу керек.

Бұл есептің шешімін Фурье әдісін пайдаланып табамыз.

1-қадам. (9.2.1) теңдеуінің шешімін түрінде іздестіреміз. және функцияларын табу үшін U(x,t) функциясының дербес туындысын тауып, (9.2.1) теңдеуіне апарып қоямыз:

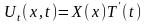
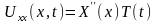
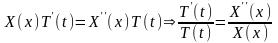(9.2.4)

(9.2.4) теңдеуінің сол жағы айнымалысына, ал оң жағы айнымалысына байланысты функциялар. және тәуелсіз айнымалылар бір-біріне тәуелсіз болғандықтан (9.2.4) теңдеуінің әрбір жағы тұрақты болуы керек. Осы тұрақтыны - деп белгілейік. ( алдындағы «-» таңбасы есепті шығаруға ыңғайлы болу үшін алынған). Онда

немесе

а) , ә) .

Енді а) және ә) жай дифференциалдық теңдеулерді шешу керек. Көңіл аударатын бір жағдай: (9.2.2) шекаралық шарттарды пайдаланып, ә) жай дифференциалдық теңдеудің жалпы шешімін емес, оның

шекаралық шарттарын қанағаттандыратын дербес шешімін іздестіреміз.

2-қадам.

Штурм-Лиувилль есебін шешеміз. Бұл есептің меншікті мәндері , ал өзіндік функциялары формуласы арқылы табылатындығы ІIІ тарауда көрсетілген болатын.

3-қадам. -параметрінің табылған мәндерін а) теңдеуіне қойып, оны шешеміз:

4-қадам. 2-3 қадамдардың нәтижесін пайдаланып (9.2.1) теңдеуінің дербес шешімдерін жазамыз:

(9.2.1) теңдеуі біртекті және сызықты болғандықтан оның дербес шешімдерінің сызықты комбинациясынан тұратын

(9.2.5)

функциясы оның шешімі болады және (9.2.2) шекаралық шарттарын қанағаттандырады.

5-қадам. (9.2.3) бастапқы шартын пайдаланып (9.2.5) теңдігіндегі коэффицентін анықтаймыз:

. (9.2.6)

(9.2.6) теңдігінен бастапқы функциясы Штурм-Лиувилль есебінің өзіндік функциялары арқылы Фурье қатарына жіктеліп тұрғанын көреміз. Бұл жағдайда Фурье қатарының коэффиценттерін

(9.2.7)

формулалары арқылы табамыз. Осы коэффициенттерді (9.2.5) теңдігіне апарып қойып, берілген (9.2.1)-(9.2.3) есебінің формальді шешімін аламыз.