7. 9. Толқын теңдеуі үшін жалғастыру әдісі. Коши есебінің шешімінің жалғыздығы.

толқын теңдеуі үшін қойылатын Коши есебін қарастырайық. (7)

теңдеуінің

(8)

бастапқы шартын қанағаттандыратын класында жататын классикалық шешімін табу керек.

Бұл есептің шешімін екі белгісіз 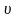және функцияларының қосындысы түрінде іздестіреміз. функциясын (7) - (8) есебіне қою арқылы

теңдіктерін аламыз. функциясын

(9)

(10)

біртекті теңдеуге қойылатын бастапқы шарттары біртекті емес Коши есебінің шешімі ретінде, ал функциясын

(11)

(12)

біртекті емес теңдеуге қойылатын бастапқы шарттары біртекті Коши есебінің шешімі ретінде таңдаймыз.

(9-(10) Коши есебінің классикалық шешімі кезде

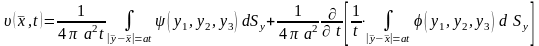(13)

Кирхгоф формуласы арқылы табылады. (11)- (12) есебінің шешімін табу үшін Дюамель белгісін пайдаланамыз. Ол үшін қосымша тағы бір

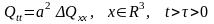(14)

(15)

есебін қарастырамыз.

жаңа айнымалысын енгіземіз. Бұл жағдайда бастапқы шарттар уақыт моментінде берілетін болады және (14)- (15) есебі

(16)

(17)

түрінде жазылады. (16)- (17) есебінің классикалық шешімін кезде Кирхгоф формуласын пайдаланып

формуласы арқылы табамыз. Бұдан қайтадан айнымалысына көшіп (14)- (15) есебінің классикалық шешімін

(18)

формуласы арқылы тауып аламыз.

Сондықтан Дюамель белгісі бойынша (11)- (12) есебінің классикалық шешімі

(19)

формуласы арқылы табылады.

жаңа интегралдау айнымалысын енгізу арқылы (19) формуласын

(20)

түрінде жаза аламыз. Мұнда ішкі интеграл центрі нүктесінде орналасқан радиусы санына тең болатын сфера бойынша, содан кейін сыртқы интеграл 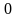-ден -ға дейін радиус бойынша интегралданатындықтан, центрі нүктесінде орналасқан радиусы санына тең болатын жабық шар бойынша интегралдауға, яғни

(21)

формуласына келеміз. Сонымен, біз төмендегідей тұжырымға келдік.

теорема. Егер 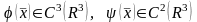, ал болса, онда

толқын теңдеуіне қойылатын Коши есебінің жалғыз, орнықты классикалық шешімі бар болады және ол

ф (22)

формуласы арқылы табылады.

8. Интегралдық теңдеулер әдісімен Гурса есебін шешу.

Екі өлшемді кеңістікте екінші ретті гиперболалық

(1)

теңдеуден функцияны →сипаттауышында

(2)

шарт берерде анықтау керек.Мұндағы , формалар өзара

(3)

үйлесімдік шарты және олар

ал теңдеудегі белгілі a,b,c,f

мұндағы жазықтықтағы шенелген аймақ . Бұл (1)-(2) есепті шешу мәселесін ∫-дық теңдеулерді шешуге келтіреміз. Ол үшін (1)-ді мына 3- теңдеулермен

түзілген (1)-ге эквивалент :

(4) теңдеулер жүйесін аламыз

(2)теңде-ден (5)-өрнегін аламыз

(4)-ң I, III теңдеулерін кескесндісінде, ал II-ні кесінді бойынша интегралдаймыз.

U=(x,y)= (6)

Бұл алынған (6) теңдеулер жүйесін шешу (1)- (2) Гурса есебі шешуімен парапар.

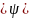Теорема: егер (1)- (2)-лер a,b,c,f C( ), [ ] және ) ) берілсе онда Гурса есебінің .