4. Даламбер формуласы

Rn+1-кеңістікте шешімі класта жататын толқын теңдеуін

қарастырайық:

U≡∆U-Utt= -F(x, t) (5 .1)

- толқындық оператор деп аталады. Нүкте x=(x1,…,xn)∈Rn, уақыт t≥0

Ω⊂Rn+1 –кез-келген аймақ, оның шекарасы S-үзік жатық бет. Бет S

координаталар осьтеріне параллель түзулермен ақырлы нүктелерде

қиылысады немесе қиылысу нүктелері түзудің кесіндісі.

Егер де функциялар U(x,t), V(x,t)∈ Cx2,,t2(Ω), онда

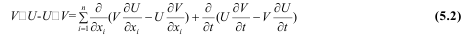
тепе-теңдіктің орындалатынын тексеру қиын емес. Теңдікті (5.2) Ω аймақ

бойынша интегралдап, Остроградский формуласын пайдалансақ, онда

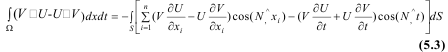
Мұндағы: N - бет, S - ішкі нормаль. Егер де нормаль N жазықтық t = 0

симметриялы бағыт ν-конормалін енгізсек, онда

Сондықтан (5.3) теңдікті мына түрде жазсақ болады:

Теңдік (5.4) толқындық оператор үшін Остроградский формаласы деп

аталады. Дербес жағдайларды қарастырайық:

а) Аймақ Ω, P(x,t) нүктеден өтетін сипаттаушылар түзулермен жəне C-

қисықпен қоршалсын.

Аймақ Ω ≡ ∆P1PP2 – үшбұрыш, ал функция V(x,t)≡1 болсын, онда (5.4)

формуладан

Сипаттаушылар P1P мен P2P - конормалдың бағыты түзулер P1P мен P2P

бағыттас болғандықтан,

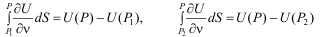
олай болса, (5.5) теңдікті түрлендіріп негізгі интегралдық формуланы

аламыз:

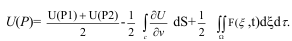
Егер де C осі x кесінді болса, яғни C≡P1P2, онда

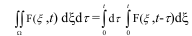
Сондықтан (5.6) формуладан,

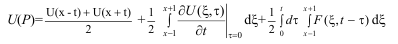
Даламбер формуласын аламыз.

5. Суперпозиция

Әдетте күрделі есептерді шешу үшін алдымен оларды қарапайым жай есептерге ажыратады. Ол есептерді шешіп жеке шешімдерін анықталып болғаннан кейін олардың қосындысы жоғарғы күрделі есептің шешімі болу жағдайы төменде келтірілген суперпозиция қағидасаларына негізделген.

1 қағида егер (x,t) =1,2,…n LU=p(x) – +q(x)*u= (1) x t>0 мынадай шарт қанағат. U(0,t)=0 U(l,t)=0 және U(x,0)= , шешім болса, U(x,t)= LU= j=1,2… U(x,0)= (x,t)= шарттарды қанағаттандыратын есептің шешімі болады

2 Егер (x,t) k=1,2…n LU=0 =0 есебінің шешімі болса u= LU=0 =0

3егер (x,t) k=1,2…n LU=0 =0 u= , =0 j=1,2… күрделі қағида

4 егер U(x,t,l) ф-я (l )

1 LU=0 =0 есептеудің шешімі болсын

2

LV=0 =0

6. Біртекті емес толқын теңдеуі үшін Коши есебі. Дюамель қағидасы

Бұл есепті шешу үшін Дюамель белгісін пайдаланамыз. Дюамель белгісі жай дифференциалдық теңдеулер үшін қолданылатын тұрақтыларды вариациялау әдісінің аналогі болып табылады. Ол біртекті емес дербес туындылы теңдеулерге қойылатын есепті біртекті теңдеулерге қойылатын есепке келтіруге мүмкіндік береді. Сондықтан әуелі Дюамель белгісіне тоқталып өтеміз. Дюамель белгісі. Егер функциясы

(1)

(2)

біртекті толқын теңдеуіне қойылатын Коши есебінің шешімі болса, онда

(3)

формуласымен анықталатын функциясы.

(4)

(5)

біртекті емес толқын теңдеуіне қойылатын Коши есебінің шешімі болады.

Дәлелдеуі. (2) бастапқы шартын ескеріп, (3) функциясы дифференциалдау арқылы

(6)

туындыларын табамыз. (6) туындыларын (4) теңдеуіне апарып қойып, функциясы (1) теңдеуінің шешімі болатындығын ескеріп

тепе-теңдігін аламыз. Бұл тепе-теңдік (3) формуласымен анықталатын функциясының (4) біртекті емес теңдеудің шешімі болатындығын көрсетеді. функциясының (5) бастапқы шартын қанағаттандыратындығы оның түрінен көрніп тұр.