Лаплас теңдеуі үшін шектік есептерді шешуде потенциалдарды қолдану әдісі.
С-контуры үшін ішкі шектік есептерді қарастырайық:
Т- облысында гармоникалық болатын, С-контурымен шектеліп, осы С контурында мына шекаралық шарттарды қанағаттандыратын u функциясын табу керек:
1-шектік
есеп: u
-Дирихденің шекаралық шарты
2-шектік
есеп:
–Нейманның шекаралық шарты
Ішкі 1- шектік есептің шешімін қос қабаттық потенциал түрінде іздейміз:
W(M)=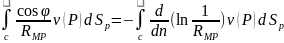
Кез-
келген
үшін
W(M)
функциясы С контурында Лаплас теңдеуін
қанағаттандырады. W(M) функциясы С
контурында үзілісті. Шекаралық шарт
орындалуы үшін
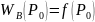болуы керек.
-
нүктесіне ішкі жағынан келгендегі қос
қабаттық потенциалдың шекті мәні. Ал
-
нүктесіне сыртқы жағынан келгендегі
қос қабаттық потенциалдың шекті мәні.
Формуланы қолдану арқылы функциясын анықтайтын формулаға келеміз:
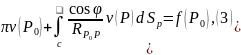
нүктесіне
сәйкес
және
S
доғаның контурларын белгілесек, (1)
теңдеуді былай жазуға болады:
-C
контурының
доғасы
Бұл- осы интегралдық теңдеудің ядросы, ол Фредгольмнің 2-текті интегралдық теңдеуі болып табылады. Сыртқы есеп үшін келесі теңдеу шығады:
2-шекті есеп үшін келесі теңдеулер шығады:
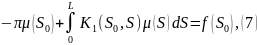-ішкі
есеп
-сыртқы
есеп
Бұл
жерде
Егер оның шешімін жай қабаттық потенциал бойынша іздесек,
u(M)=