Шар үшін Дирихле есебінің шешуі. Пуассон формуласы.
Дөңгелек үшiн Дирихле есебiн қарастырайық:
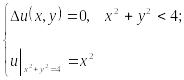
Шешуi Есептiң шешiмiн
түрiнде iздейiк. Осы қатарды шекаралық шартқа қойып, мынадай теңдiк аламыз
Мұнда
Осы
теңдiктiң екi жағындағы Фурье коэффициенттерiн
салыстырып барлық Ak
және
Bk
коэффициенттерi
және
болғанда нөлге тең екенiн көремiз.
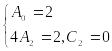
Осыдан
,
болады
да есептiң шешiмiн мына түрде жазамыз.
айқын түрдегі шешімдерді аламыз.
23. Лаплас теңдеуі үшін шекаралық есептің шешімінің жалғыздығы.
Th-1.
Дирихле
ішкі есебінің жалғыздығы
,
есебінің шешімі жалғыз.
Дәлелденуі:
Кері жоримыз. Есептің шешімі
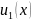және
.
)=0
Th-2.
Дирихле
сыртқы есебінің жалғыздығы
,
есебінің шешімі жалғыз.
Дәлелденуі:
Инверсиялық және Кельвин түрлендірулері
бойынша а=1 деп алайық,
,
,
мұндағы
-
есебіндегібелгісіз
функция.
Ішкі
есеке келтірдік
Демек
үшін ішкі есеп алдық. Оның шешімі жалғыз.
24. Көлемдік және беттік потенциалдар
Дирихле және Нейман есептерін шар және жартылай кеңістіктен басқа облыстарда қарастыру үшін
интегралдарын
бөлек – бөлек қарастыру керек.
және
интегралдарын сәйкесінше көлемдік,
қос қабаттық, жай қабаттық потенциалдар
деп, ал
және
функцияларын олардың тығыздықтары
деп
атайтындығын өткен дәрісте айтқан
болатынбыз.
14.1. Көлемдік потенциал.
(14.1.1)
көлемдік
потенциалын қарастырайық, мұндағы
-
ақырлы облыс.
- функциясы
облысында шенелген және интегралданатын
болсын деп ұйғарайық. Егер
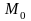нүктесі
облысында жатпаса, онда (14.1.1) – интегралы
меншікті
интегралды
анықтайды. Бұл жағдайда
функциясы үзіліссіз және оның барлық
ретті дербес туындылары болады. Бұл
туындыларды интеграл белгісі астынан
дифференциалдау арқылы табуға болады.
Осылармен қатар
функциясы кеңістіктің
облысының нүктелерінен басқа нүктелерінде
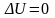- Лаплас теңдеуін қанағаттандырады.
Енді нүктесі шексіздікке кез-келген бағыт бойынша ұмтылған кезде, функциясы нөлге ұмтылатындығын, яғни
теңсіздігін қанағаттандыратындығын көрсетейік.
Декарттық
координаталар жүйесінің бас нүктесі
-
облысында жатсын. Онда
немесе
теңсіздігі орындалады.
-
облысының диаметрін
-
деп белгілейік. Онда
болады.
- нүктесі бас нүктеден
болатындай өте алыс орналасқан деп
ұйғарайық. Бұл жағдайда
немесе
теңсіздігі орындалады. Осы теңсіздікті ескеріп,
теңсіздігін аламыз. Мұндағы
Сонымен, - көлемдік потенциал кеңістіктің - облысының сыртында гармониялық функция.
Енді нүктесі облысының ішінде жатсын. Онда (14.1.1) интегралы меншікті емес интегралды анықтайды. тығыздығы шенелген болғандықтан, (14.1.1) меншікті емес интегралының жинақталатындығы шығады, өйткені
.
Сонымен қатар, потенциалы және оның бірінші ретті дербес туындылары кеңістіктің барлық нүктелерінде үзіліссіз және оларды интеграл белгісінің астынан дифференциалдау арқылы табуға болатындығын көрсетуге болады.
Көлемдік потенциалдың екінші ретті дербес туындылары бар болу үшін оның тығыздығына қосымша шарттар қою қажет.
14.1.1-теорема.
Егер тығыздығы
-
тұйық облысында үзіліссіз және
- облысының ішкі нүктелерінде оның
үзіліссіз бірінші ретті дербес туындылары
бар болса, онда (14.1.1) көлемдік потенциалының
облысының ішкі нүктелерінде үзіліссіз
екінші ретті дербес туындылары бар
болады және ол
Пуассон теңдеуін қанағаттандырады.
Сонымен,
егер
болса, онда
көлемдік потенциалы
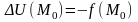
Пуассон теңдеуінің дербес шешімін анықтайды.
14.2.
Ляпунов беті. Жай
және қос қабаттық потенциалдардың
қасиеттерін қатаң анықтау үшін осы
қабаттар орналасқан беттер қандай да
бір шарттарды қанағаттандыруы қажет.
Тұйық
беті төмендегідей үш шартты қанағаттандыратын
болсын:
1. - бетінің кез-келген нүктесінде жанама жазықтық жүргізуге болады;
2.
- бетінің кез-келген нүктесінің маңайына
радиусы
нүктесіне байланысты емес, ішіне
бетінің тек
нүктесі арқылы өтетін
- нормаль векторына паралелль болатын
түзулердің саны бірден артық болмайтын
бөлігі жататын, сырттай шар құруға
болады;
3.
Егер
-
бетінің
нүктелері арқылы жүргізілген нормалдардың
арасындағы сүйір бұрыш, ал
-
осы нүктелердің ара-қашықтығы болса,
онда
теңсіздігі орындалатын болады;
Мұндай бетін Ляпунов беті деп атайды.
-
Ляпунов бетінің кез-келген нүктесі
болсын. Бірінші шарт
-
нүктесін бас нүктенің орнына осы нүкте
арқылы өтетін жанама жазықтық ретінде
жазықтығын,
ал нормаль түзуді
өсі
ретінде алып, Ляпунов бетінің
-
нүктесінде
-
декарттық координаталар жүйесін құруға
мүмкіндік береді. Екінші шарт Ляпунов
бетінің центрі
нүктесінде, радиусы
-
санына тең болатын
сферасының ішінде жататын
бөлігінің
жоғарыда анықталған декарттық
координаталар жүйесінде анықталатын
теңдеуін
айнымалысы бойынша шешуге, яғни
түрінде жазуға болатындығын көрсетеді.
Үшінші шарттан
және
дербес
туындыларының
аргументтері бойынша үзіліссіз
болатындығы шығады.
14.3.
Қос қабаттық потенциал. Ляпунов
бетінде берілген
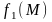тығыздығы
үзіліссіз болатын
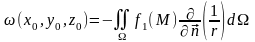(14.3.1)
қос қабаттық потенциалын қарастырайық. Қос қабаттық потенциалдың бетінде жатпайтын нүктелерде барлық ретті туындылары бар болады және ол Лаплас теңдеуін қанағаттандырады. Шексіздікте қос қабаттық потенциалдың нөлге ұмтылатындығын көрсетейік. Ол үшін бас нүктені бетімен шенелген облысының ішінен алайық. Онда
немесе
теңсіздігі
орындалады. Бас нүктеден
бетінде жататын нүктелерге дейінгі
ара-қашықтықтардың ең үлкенін
деп
белгілейік. Онда
болады.
-
нүктесі бас нүктеден
болатындай өте алыс орналасқан деп
ұйғарайық. Бұл жағдайда
немесе
теңсіздігі
орындалады.
векторымен
бетінің
нүктесіне сырттай жүргізілген
векторының арасындағы бұрышты
деп белгілейік. Онда (14.3.1) формуласын
теңдігі түрінде жазуға болады. Осыдан
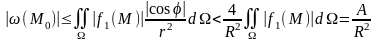
теңсіздігін аламыз. Мұндағы
Сондықтан
қос қабаттық потенциал шексіздікте
сияқты нөлге ұмтылады.
Ілгеріде
біз қос қабатты потенциалдың қасиеттерін
дәлелдеусіз келтіреміз.
нүктесі
бетінде жататын болсын. Онда
өрнегінің мәні
мен
беттескен кезде нөлге айналады. Бұл
жағдайда (14.3.1) интегралы жинақталатын
меншіксіз интеграл болатындығын
көрсетуге болады. Сонымен қос қабаттық
потенциал кеңістіктің барлық нүктелерінде
анықталады.
Егер
нүктесі
бетінде жатса, онда (14.3.1) интегралының
нүктесіндегі мәнін қос
қабаттық потенциалдың тура мәні
деп атайды.
-
бетінде жататын
нүктесіне жақындайтын, бірақ
бетіне жатпайтын нүкте болсын. Егер
жақындасу
қос қабаттық потенциалдың қандайда бір
ақырлы шекке ұмтылуын қамтамасыз ететін
болса, онда біз қос қабаттық потенциал
нүктесінде шектік мәнін қабылдайды
дейміз. Қос қабаттық потенциалдың тура
мәнімен шектік мәні жалпы жағдайда
бір-бірімен беттеспейді. Әлбетте,
нүктесінің
бетіне іштей немесе сырттай жақындауына
байланысты
қос қабаттық потенциалдың шектік мәндері
әртүрлі болады және олар оның тура
мәнімен беттеспейді. Нақтырақ айтқанда
төмендегідей тұжырым орындалады.
14.3.1
- теорема.
нүктесі
бетінде жатқан
нүктесіне іштей немесе сырттай ұмтылған
кезде
қос қабаттық потенциалдың шегі бар
болады. Егер
қос қабаттық потенциалдың сыртқы, ал
-
ішкі шектік мәні болса, онда
теңдіктері орындалады.
Сонымен, - қос қабаттық потенциалы үзілісті функция.
14.4. Жай қабаттық потенциал. Ляпунов бетінде берілген, -тығыздығы үзіліссіз болатын
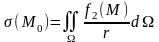(14.4.1)
жай
қабаттық потенциалын қарастырайық. Жай
қабаттық потенциалдың
бетінде жатпайтын нүктелерде барлық
ретті туындылары бар болады және ол
Лаплас теңдеуін қанағаттандырады. Дәл
14.3-пунктінде көрсетілгендей шексіздікте
жай қабаттық потенциалдың
сияқты
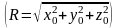нөлге ұмтылатындығын көрсетуге болады.
Тығыздығы үзіліссіз функция болатын
жай қабаттық потенциалдың кеңістіктің
барлық нүктелерінде үзіліссіз болатындығын
дәлелдеуге болады. Жай қабаттық
потенциалдың нормаль бағыты бойынша
алынған туындысын қарастырайық.
бетінде жататын кез келген нүктені
,
ал осы нүкте арқылы өтетін сыртқы
нормальді
деп белгілейік. Жай қабаттық потенциалдың
бетінде жатпайтын
нүктесінде
– сыртқы нормаль бойынша алынған
туындысы
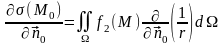(14.4.2)
формуласы арқылы табылады.
Әлбетте, нүктесі бетінде жататын нүктесімен беттескен кезде де (14.4.2) интегралы өзінің мағынасын сақтайды және ол нүктесінде үзіліссіз функция болады.
және
деп сәйкесінше нүктесі бетінде жататын нүктесіне іштей және сырттай жақындаған кездегі жай қабаттық потенциалдың шектік мәндерін белгілейік.
14.4.1-теорема. Егер үзіліссіз функция болса, онда
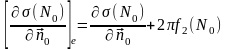
(14.4.3)
теңдіктері орындалады.
(14.4.3)-формуласынан жай қабаттық потенциалдың нормаль бағыты бойынша алынған туындысының секірмесінің шамасы
-
болатындығы шығады.