4. Математикалық физика теңдеулері

1. Математикалық физиканың негізгі теңдеулері. МФТ келтірілетін физикалық есептер.

2. Коши және басқа да шекаралық есептердің қойылымы.

3. Екі немесе одан көп айнымалылы параболалық, гиперболалық және эллиптикалық теңдеулерді канондық түрге келтіру және классификациялау; жалпы шешім.

4. Толқын теңдеуі үшін Коши есебі. Даламбер формуласы. Тура және кері толқындар.

5. Суперпозиция қағидалары.

6. Біртекті емес толқын теңдеуі үшін Коши есебі, Дюамель қағидасы.

7. Толқын теңдеуі үшін жалғастыру әдісі. Коши есебінің шешімінің жалғыздығы.

8. Интегралдық теңдеулер әдісімен Гурса есебін шешу.

9. Толқын теңдеуі үшін Коши есебінің шешімінің жалғыздығы.

10. Толқын теңдеуі үшін шеттік есебінің шешімінің жалғыздығы және функциялар қасиеттері.

11. Біртекті теңдеу үшін шекаралық есептерді Фурье әдісімен шешу. Штурма–Лиувиль есебінің меншікті мәні мен меншікті функциясы, қасиеттері.

12. Біртекті емес теңдеу үшін шекаралық есептерді Фурье әдісімен шешу.

13. Жылуөткізгіштік теңдеуі. Коши есебі. Пуассон формуласы.

14. Біртексіз жылуөткізгіштік теңдеуігің Коши есебінің шешімі.

15. Жылуөткізгіштік теңдеуі үшін аралас есепті Фурье тәсілімен шешу.

16. Жылуөткізгіш теңдеу үшін Коши есебін айнымалыға жіктеу–Фурье тәсілімен шешу.

17. Жылуөткізгіштік теңдеуі үшін Грин функциясы әдісі.

18. Жылуөткізгіштік теңдеуі үшін экстремум қағидасы және салдары.

19. Лаплас теңдеуі. Фундаментальды шешім. Гармоникалық және аналитикалық функциялар.

20. Лаплас операторы үшін Грин формулалары. класта функцияның интегралды өрнектелуі.

21. Гармоникалық функциялардың қасиеттері.

22. Шар үшін Дирихле есебінің шешуі. Пуассон формуласы.

23. Лаплас теңдеуі үшін шекаралық есептің шешімінің жалғыздығы.

24. Көлемдік және беттік потенциалдар.

25. Лаплас теңдеуі үшін шектік есептерді шешуде потенциалдарды қолдану әдісі.

1. Математикалық физиканың негізгі теңдеулері. Мфт келтірілетін физикалық есептер

U=U(x,y) бұл фун-я үшін (1) теңд қарастырайық.

Бұл теңдеу айн немесе тұрақты коэф. Типке ажырату үшін дискриминант табамыз.

Егер n>2 (1) (2) x(x1,…xn) бұл теңд-і типтерге ажырату үшін теңд жоғ. ретті мүш с-с. Q(l1,l2…ln)= квадраттық көпмүшелікті құрамыз. Бұл көпмүшелікті емес сызықтың түрленген нәтижесінде (3) канондық түрде аламыз. - байл тұр. шамалар

1. Егер барлық лер Оге тең емес және бірдей таңбалы болса, (2) элиптикалық д.а жылу құб. теңд

2. Ал егер тең емес О бірақ кейбірі қалғанымен салыстырғанда кері таңбалы болса (2) гипербалық д.а

(5) лаплас операторы

3. Ал егер біреуі немесе бірнешеуі Оге тең болса (2) параболалық теңд д.а

U=u(x) u(x)=-f(x) пуассон

2. Коши және басқа да шекаралық есептердің қойылымы.

Теңдеулерге есеп қою. Гиперболалық теңдеуге

Аралас есеп u(x,t) тербелістің шамасын анықтау керек

J1 +u |x=0 = M1(t)

J2 +u |x=e = M2(t) (7)

U(x,0)=

(x,0)= бастапқы шарттар (8)

2) коши есебі шексіз аймақ үшін қойылады. U(x,0)= , (x,0)= x

Параболалық

Аралас ,(7) түріндегі U(x,0)= бастапқы шарт және Коши есебі (шексіз аймақ үшін) U(x,0)= , x U(x,t)- ны анықтау

3. Элиптикалық

1 дирихле U=u(x) u(x)=-f(x) осыдан u(x)|=f(x) (11) шартты қанағат u(x) т.к.

2) нейман U=u(x) u(x)=-f(x) |s=f(x) шартты қана u(x) т.к

3) жалпылама аралас есеп U=u(x) u(x)=-f(x)

Коши есебі t=0 мезетте ғана берілмей кеңістіктің қандай да бір бетінде немесе сызықта беріледі.

3. Екі немесе одан көп айнымалылы параболалық, гиперболалық және эллиптикалық теңдеулерді канондық түрге келтіру және классификациялау; жалпы шешім.

2-ретті сызықтық дербес

теңд канондық түрге келтіру

N=2 U=U(x,y) фун-я үшін (2.2.1)

тәуелді немесе тұр шама

(3)

(3)-ті ((2.2.1))-4 сипаттаушы теңд. Д.а.

(4)

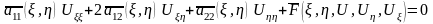, (2.2.3)

мұндағы

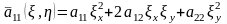
(2.2.4)

гиперболалық типті теңдеу үшін жалпы интегралдары нақты және әр түрлі. Сондықтан гиперболалық типті теңдеулердің екі әртүрлі нақты сипаттамалары болады.

түрлендіруін алайық. Мұндағы және бірінші ретті дербес туындылы дифференциалдық теңдеудің үзіліссіз дифференциалданатын шешімдері. Онда (2.2.4) теңдігінен (2.2.3) теңдеуіндегі

болатындығы шығады. нүктесінің маңайында болмайды, өйткені кері жағдайда немесе болады. (2.2.3) теңдеуін коэффициентіне бөліп

(2.2.15)

теңдеуін аламыз. (2.2.15) теңдеуі (2.2.1) гиперболалық типті теңдеудің канондық түрі.

Егер (2.2.1) теңдеуі функциясы мен оның бірінші ретті дербес туындыларына байланысты сызықты болса, онда түрлендірілген теңдеу де сызықты болады, яғни бұл жағдайда гиперболалық типті теңдеудің түрі

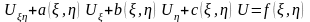
түрінде анықталатын болады.

(2.2.15) теңдеуіндегі және айнымаларының орнына

жаңа айнымалыларын еңгізу арқылы (2.2.1) гиперболалық типті теңдеуінің басқа

(2.2.16)

түріндегі канондық түрін алуға болады.

Екінші жағдай. облысында жатқан кез келген нүктелер үшін болсын. Онда облысында (2.2.1) теңдеуі параболалық типті теңдеу болады. Ұйғарым бойынша (2.2.1) теңдеуінің және коэффициенттері бірдей уақытта барлығы нөлге айналмайды, сондықтан теңдігінен облысының әрбір нүктесінде және коэффициенттерінің кем дегенде біреуі нөлден өзгеше болады.

(2.2.17)

жүйесін аламыз. (2.2.17) жүйесінің анықтауышы

болғандықтан, (2.2.17) жүйесінің тек нөлдік шешімі болады. Онда маңайында болады. Бұл маңайында орындалатын теңсіздігіне қайшы. Алынған қайшылық шынында маңайында коэффициентінің нөлге айналмайтындығын көрсетеді. (2.2.3.) теңдеуін коэффициентіне бөліп

(2.2.18)

теңдеуін аламыз. (2.2.18) теңдеуі (2.2.1) параболалық типті теңдеудін канондық түрі.

Үшінші жағдай. облысында жатқан кез келген нүктелер үшін болсын. Онда облысында (2.2.1) теңдеуі эллиптикалық типті теңдеу болады. (2.2.1) теңдеуінің және коэффициентері облысында аналитикалық функциялар болсын деп ұйғарайық. Онда (2.2.12) мен (2.2.13) теңдеулерінің оң жағында тұрған функциялар да және аргументтері бойынша аналитикалық функциялар болады. Сондықтан, Коши – Ковалевская теоремасы бойынша (2.2.12) бірінші ретті жай дифференциалдық теңдеуінің болмайтын нүктесінің маңайында теңсіздігін қанағаттандыратын комплекс мәнді аналитикалық шешімі бар болады.(2.2.2.) түрлендіруі ретінде

(2.2.19)

түрлендіруін алайық. Енді (2.2.19) түрлендіруінің Якобианы

маңайында нөлге айналмайтынын көрсетейік. Қарсы жорыйық, яғни (2.2.19) түрлендіруінің Якобианы маңайының кейбір нүктесінде нөлге айналатын болсын.Онда

теңдігінен

(2.2.20)

теңдігін аламыз. функциясы маңайында аналитикалық функция болғандықтан, бұл функция үшін Коши-Риман шарты орындалады

Сонымен, . Осы функцияны (2.2.6) теңдеуіне апарып қойып

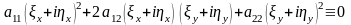
тепе-теңдігін аламыз. Тепе-теңдіктің нақты және жорамал бөліктерін бөліп

теңдіктеріне келеміз. Кейінгі теңдіктерден және екендігі шығады. Сонымен қатар болуы керек, кері жағдайда (2.2.5) теңдігіне қайшылыққа келеміз. (2.2.3) теңдеуін коэффициентіне бөліп

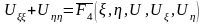(2.2.21)

теңдеуін аламыз. (2.2.21) теңдеуі (2.2.1) эллиптикалық типті теңдеудің канондық түрі.