20.Функцияларды дәрежелік қатарларға жіктеу.

f (x) функциясы a -R <x <a +R аралығында анықталған және кез келген ретті туындылары бар болсын. Тейлор формуласы бойынша

мұндағы , µ=a+ (x-a), Егер n , (x) 0 болса, онда

қатары Тейлор қатары деп аталады. (x) - Тейлор қатарының қалдық мүшесі дейді. Егер a =0 болса, онда Тейлор қатары Маклорен қатары деп аталады да

түрінде жазылады. Егер f (x) функциясы (a-R;a+R) аралығында анықталып, кез келген n үшін теңсіздігі орындалса (мұндағы М-оң тұрақты сан), онда осы функция Тейлор қатарына жіктеледі. Кейбір функциялардың Маклорен қатарына жіктелуін көрсетейік:

1. ( )

2. ( )

3. ( )

4. ( )

5. ( )

6. Соңғы жіктеуде:

болса, онда .

-1< болса, онда .

болса, онда .

21.Қос интегралдаудың негізгі қасиеттері.

Түйық сызықпен қоршалған , жазықтығында жатқан D облысында анықталған үздіксіз функцияны қарастырайық. 0сы облысын n бөлшектерге бөлеміз, ол бөлшектерінің аудандарын деп белгілейік. Әрбір бөлшек ішінде жатқан кез келген нүктені алайық , осы нүктелерге сәйкес функция мәндерін есептеп интегралдық қосындыны құрайық. осы өрнектің шегі, егер , бір тиянақты шекке ұмтылса , онда ол шекті қос интеграл деп атайды, яғни

Қос интегралдың қасиеттері.

а) тұрақты көбейткішті интеграл белгісінің сыртына шығаруға болады .

б) және функциялардың қосындысының интегралы интегралдар қосындысына тең, яғни

в) Егер интегралдау D облысы екі D₁, және D₂ облысынан құралатын болса, онда

.Қос интегралды есептеу . Айталық D облысы сызықтармен шектелген болсын, және .Енді қос интегралдың есептеуі қайталап интегралдауға келтіріледі, яғни мұнда -ішкі интеграл деп атайды. Қос интегралды есептегенде бірінші ішкі интегралды есептейді. Бұл жағдайда х-тұрақты деп санайды.

Мысал. қос интегралды есептейік. Мұнда D облысы х=0 сызықтармен шектелген.

Шешімі

22.Қос интегралдауда және үш еселі интегралдауда айнымалыны ауыстыру.

Екі еселі интеграл қарастырайық.f(x,y) функциясы шенелген тұйық D аймағында үзіліссіз. (8.4) формулалары арқылы жаңа u және v аргументтеріне көшіп (8.4) теңдеулер жүйесінен деп есептеп, u=u(x,y),v=v(x,y)(8.5) функциялары анықталады. нүктесіне u,v координаттар жазықтығында нүктесі сәйкес келеді. Онда (8.4) формуласындағы функциялардың дербес туындылары бар болады да, мына анықтауыш ,сонда (8.6) теңдігі орындалады.J(u,v)-ны x=x(u,v),y=y(u,v) функцияларының Якобинаны деп атайды. Егер (8.4) формуладан полярлық координаталарға көшетін болсақ, яғни (8.7) деп алсақ, онда, (8.7) алмастыруының Якобианы екенін ескеріп, (8.8) теңдігіне келеміз.

Мысал 3 , D - бірінші квадрантта жататын дөңгелегінің бөлігі . Осы интегралды есептеу керек.Шешуі формулаларынан ; .

Сондықтан, Үш еселі интегралдауда айнымалыны ауыстыру.

1)Кеңістіктегі қисық сызықты координаттар.

V мен V^’ аймақтары нүктелерінің арасында бір мәнді және үзіліссіз сәйкестік бар болсын. Сонымен бірге тура сәйкестік

(8.10)

ф ормулаларымен анықталып, кері сәйкестік

9-сурет

(8.11)

формуларымен анықталсын. (8.10) және (8.11) функцияларының өздері де, бірінші ретті дербес туындылары да үзіліссіз деп жориық. Сонда үзіліссіз якобиандар мен бар болады.

=

J – (8.10) функциялардың якобианы деп аталады.

2) Кеңістіктегі цилиндрлік координаттар. Декарттық координаттар жүйесінде нүктесі беріліп, оның Оху жазықтығындағы проекциясы М₁ нүктесі болсын. М нүктесі оның аппликатасы z және М₁ өзінің полярлық кординаттары мен арқылы анықталса, онда шамалары М нүктесінің цилиндрлік координаттары болады. М нүктесінің декарттық және цилиндрлік координаттарының арасындағы байланыс мына формулалармен анықталады (10-сурет): x,y,z координаттарын координаталарымен ауыстыру якобианы: болады.Сондықтан 3 еселі интегралда айнымалы а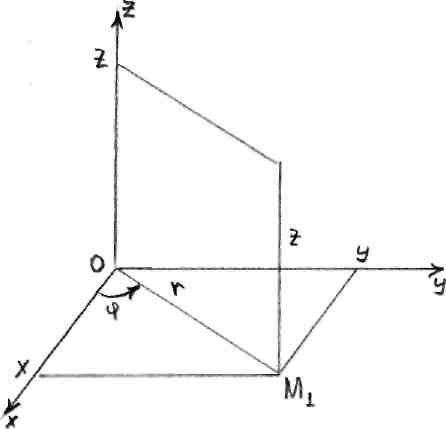 уыстыру

10-сурет .

3) Сфералық координаттар. Оxyz кеңістігінде М нүктесінің орнын:

а) О нүктесінен М нүктесіне дейінгі қашықтық ;

б) ОМ кесіндісі мен Оz өсінің оң бағыты арасындағы бұрыш ;

в) ОМ кесіндінің Оху жазықтығындағы проекциясы ОМ₁ мен Ох өсінің оң бағыты арасындағы бұрыш арқылы анықтасақ, онда осы шамалары М нүктесінің сфералық координаттары болады. М нүктесінің декарттық және сфералық координаттар арасындағы байланыс мына формулар арқылы анықталады (суретке қара):

1 1-сурет

Декарттық координаттарды сфералық координаттарға ауыстыру якобианы былайша анықталады:

.