5)Кесіндідегі үзіліссіз функциялардың қасиеті

Теорема(4-қ):(Больцано-Коши т/ы) F(x) функциясы [a; b] кесіндісінде анықталып, үзіліссіз болсын және оның ұштарында әр түрлі таңба қабылдасын.Онда (a;b) аралығында f(x₀)=0 болатын x₀ нүктесі табылады. Теорема(5-қ): F(x) функциясы [a; b] кесіндісінде анықталып үзіліссіз болсын. Онда f(a) және f(x) нүктелерінің арасында орналасқан кез келген С саны үшін f(x₀)=C болатын x₀∊[a;b] нүктесі табылады. Теорема(6-қ):(Вейерштрасстың 1-ші т/ы) F(x) функциясы [a; b] кесіндісінде анықталып үзіліссіз болсын. Онда бұл функция сол кесіндіде шенелген. Теорема(7-қ):(Вейерштрасстың 2-ші т/ы) F(x) функциясы [a; b] кесіндісінде анықталып үзіліссіз болсын. Онда функция [a; b] кесіндісінде өзінің ең үлкен және ең кіші мәндерін қабылдайды, яғни кез келген x₀∊[a;b] нүктесі үшін f(x₁)≤f(x) ≤f(x₂) теңсіздіктері орындалады. Мысалы: Функциясын үзіліссіздікке зерттеп графигін салу керек.Функцияны нүктелерінде үзіліссіздікке зерттейік, ол үшін сәйкес біржақты шектермен функцияның мәндерін табамыз. нүктесінде: Сонымен, бұл нүктеде яғни, функцияның бірінші текті үзілісі бар және сол жағынан үзіліссіз. F(x) функциясының нүктесіндегі секірмесі:

6)Функцияның үзіліссіз нүктелері және оларды классификациясы.

Функцияның үзіліс нүктелері. Анықтама: x₀ нүктесі F(x) функциясының анықталу аймағына тиісті немесе сол аймақтың шектік нүктесі болсын. Егер F(x) функциясы x₀ нүктесінде үзіліссіз болмаса, онда сол нүкте F(x) функциясының үзіліс нүктесі деп аталады; Үзіліс нүктелер бірінші текті және екінші текті деп бөлінеді; Анықтама: x₀ нүктесі арқылы біржақты және шектері бар болса, бірақ олар өзара тең емес немесе біржақты шектер өзара тең, ал функцияның сол нүктедегі мәні біржақты шектермен беттеспесе, онда x0 нүктесі бірінші текті үзіліс нүкте деп аталады; Егер x0 нүктесінде арқылы шек бар болса, ал f(x₀) анықталмаған немесе болса, онда бұл нүкте жөнделетін үзіліс нүктесі деп аталады. F(x) функциясының, жөнделетін үзіліс нүктесі болмайтын, бірінші текті үзіліс нүктелері функцияның секірме нүктелері деп аталады; Егер x0 - функцияның секірме нүктесі болса, онда айырмасы нөлге тең емес және F(x) функциясының x0 нүктесінде секірмесі деп аталады; Анықтама: егер x0 нүктесінде және біреуі бар болмаса, онда x₀-екінші текті үзіліс нүктесі деп аталады.

7)Дифференциалданатын функциялардың негізгі қасиеттері.

Анықтама. Функцияның туындысы мен аргумент өсімшесінің көбейтіндісі дифференциал деп аталады және мына түрде жазады: .

Анықтама. f(x) функциясы x нүктесінде дифференциалданады, егер оның осы нүктеде дифференциалы болса. Егер f(x) функциясы дифференциалданатын болса, онда ол міндетті түрде үзіліссіз болады.

Дифференциалдың қасиеттері:

Негізігі элементар функциялардың туындыларын біле тұрып, біз еш қиындықсыз осы функциялардың дифференциалдарының кестесін құрастыра аламыз.

Айталық, , , т.с.с.

Арифметикалық амалдар нәтижелерінің дифференциалдары:

;

;

.

Күрделі функцияның дифференциалы:

Айталық, және - үзіліссіз функциялар және олардың туынддылары: , . Егер белгілесек, онда . Екі жағын dx-ке көбейтеміз: , ал , олай болса, .

8)Бір айнымалы функция үшін Тейлор формуласы. Айталық y=f(x) функциясы бір аралықта анықталған болып, осы аралықтан алынған х=а нүктесінде n+1-ші ретке дейін туындылары бар болсын. Мұндай шарттар орындалғанда функцияның ролін көпшілік жағдайда n-ші дәрежелі көпмүшелік атқарады Осы көпмүшелікті мына түрінде алайық. Бұл көмүшелік пен функцияның арасында келесі шарттар орындалатын болсын Сонғы (5.26) теңдіктер орындалса, онда (5.25) көпмүшелік х=а нүктесінің аймағында y=f(x) функцияны көпмүшелікпен алмастыруға болады.

Көпмүшеліктің С₀ , C₁ , C₂ …, C_n коэффициенттерін, (5.26) теңдіктерін пайдаланып, анықтайық. Ол үшін (5.25) көпмүшеліктің туындыларын табайық:

Егер (5.26) теңдіктерін пайдалансақ

Осы теңдіктерден аталған коэффициенттерді табамыз:

Осы коэффициенттерді (5.28) формулаға қойсақ формула анықталады.

R_n(x) арқылы f(x) функция мен P_n(x) көпмүшеліктін айырмасын белгілесек

белгілесек, мұнда

C=a+ (x+a), 0< <1 онда

Осы формуланы Тейлор формуласы дейді. Мұнда қалдық мүшені түрінде жазылады. Егер Тейлор формуласында а=0 деп алсақ, онда (5.30)Бұл формуланы Маклорен формуласы деп айталады. Тейлор формуласын қолдану мысалдар

1) функциясы берілсін.

Бұл функцияның == онда

Енді Маклорен формуласын пайдалансақ

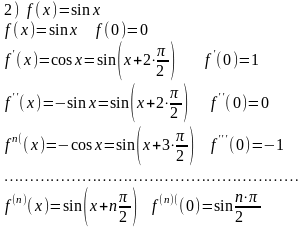
Маклорен формуласы арқылы

мұнда

3) f(x)=cosx, онда Маклорен формуласын пайдланып анықтаймыз

Мұнда