2. Логика и исчисление предикатов

1. Записать на языке предикатов

5. для любого числа можно найти большее число;

x – любое число;

y – y>x.

14. «Все счастливые семьи похожи друг на друга, каждая несчастливая семья несчастлива по-своему»

P – множество семей

x – счастливые семьи

y – несчастные семьи

2. Получить множество дизъюнктов.

5. x P(x)  x R(x) ≡ {вынос квантора за скобки} ≡ x (P(x)  R(x))

3. Автоматическое доказательство теорем

1. Преобразовать теоремы в вопросы и получить ответы с помощью метода резолюции.

1.4. А1: Если робот обработал деталь, то ее забирает штабелер.

А2: Если деталь поступила на обработку, то ее обработает робот.

А3: Если человеку нужна деталь, то она поступит на обработку.

А4: Человеку нужна втулка.

Вопрос: Что заберет штабелер.

Запишем аксиомы и теоремы на языке предикатов первого порядка.

А1:

А2:

А3:

А4:

В:

Получим дизъюнкты.

1. 

2)

3)

4)

Чтобы получить дизъюнкты из вопроса, надо взять ее отрицание.

5)

Таким образом, получаем систему дизъюнктов:

Д1:

Д2:

Д3:

Д4:

Д5:

Вывод:

1. Унифицируем Д3 и Д4: , получаем

2. Получаем резольвенту Д3-Д4: , обозначим ее как Д6

3. Унифицируем Д2 и Д6: , получаем

4. Получаем резольвенту Д2-Д6: 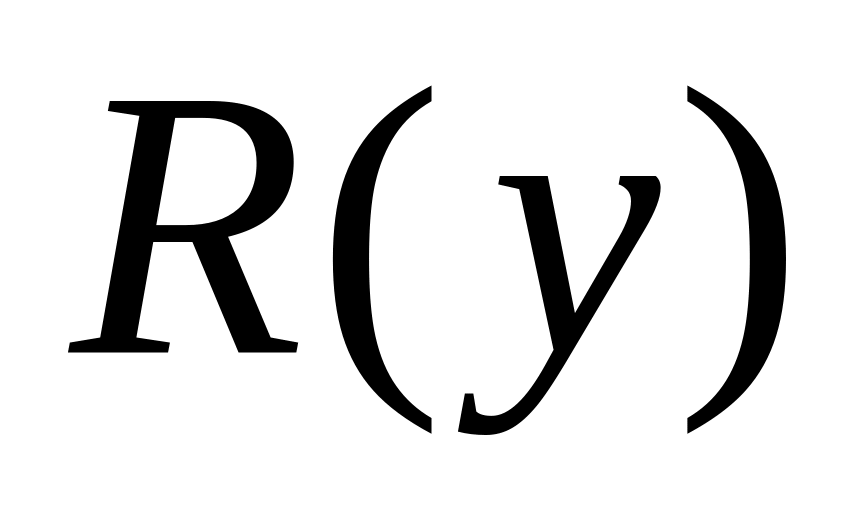, обозначим ее как Д7

5. Унифицируем Д1 и Д7: , получаем

6. Получаем резольвенту Д1-Д7: , обозначим ее как Д8

7. Унифицируем Д5 и Д8: , получаем

8. Получаем резольвенту Д5-Д8: 

Ответ можно интерпретировать следующим образом: штабелер заберет деталь.

2. Доказать теорему

2. A1:

T:

Получим дизъюнкты.

Д1:

Д2:

Чтобы получить дизъюнкты из теоремы, надо взять ее отрицание.

Д3:

Д4:

Д5:

Таким образом получаем систему дизъюнктов:

Д1:

Д2:

Д3:

Д4:

Д5:

Вывод:

1. Унифицируем Д1 и Д3: , получаем

2. Получаем резольвенту Д1-Д3: , обозначим ее как Д6

3. Унифицируем Д6 и Д4: , получаем

4. Получаем резольвенту Д6-Д4: , обозначим ее как Д7

5. Унифицируем Д7 и Д5: , получаем

6. Получаем резольвенту Д7-Д5:  (пустой дизъюнкт)

Теорема доказана.

4. А1: Т:

Получим дизъюнкты.

Д1:

Чтобы получить дизъюнкты из теоремы, надо взять ее отрицание.

Д2:

Таким образом получаем систему дизъюнктов:

Д1:

Д2:

???

Вывод:

1. Унифицируем Д1 и Д2: , получаем

2. Получаем резольвенту Д1-Д2:

4. Теория алгоритмов

1. Построить машину Тьюринга, которая:

1.6. В последовательности, состоящей из 0 и 1 сдвинуть слово, состоящее из 1 влево.

1

1

1

Программа:

(Если в воспринимаемой ячейке символ 0, и МТ находится в состоянии q_1, то состояние не меняется, символ не меняется, УУ сдвигается вправо).

(Если в воспринимаемой ячейке символ 1, и МТ находится в состоянии q_1, то это значит, что УУ находится на начале слова, состояние меняется на q₂, символ не меняется, УУ сдвигается влево).

( Если в воспринимаемой ячейке символ 0, и МТ находится в состоянии q_2, то это значит, что УУ находится в ячейке, с которой должно начаться слово, состояние меняется на q₃, символ меняем на 1, УУ сдвигается вправо).

( Если в воспринимаемой ячейке символ 1, и МТ находится в состоянии q_3, то это значит, что УУ передвигается по слову, состояние не меняется, символ не меняется, УУ сдвигается вправо).

( Если в воспринимаемой ячейке символ 0, и МТ находится в состоянии q_3, то это значит, что УУ дошло до ячейки, которая следует после конца слова, состояние меняется на q₄, символ не меняется, УУ сдвигается влево).

( Если в воспринимаемой ячейке символ 1, и МТ находится в состоянии q_4, то это значит, что УУ дошло до конца слова, состояние меняется на заключительное, символ меняется на 0, УУ останавливается).

В виде таблицы эту программу можно записать следующим образом:

а	q1	q2	q3	q4
0
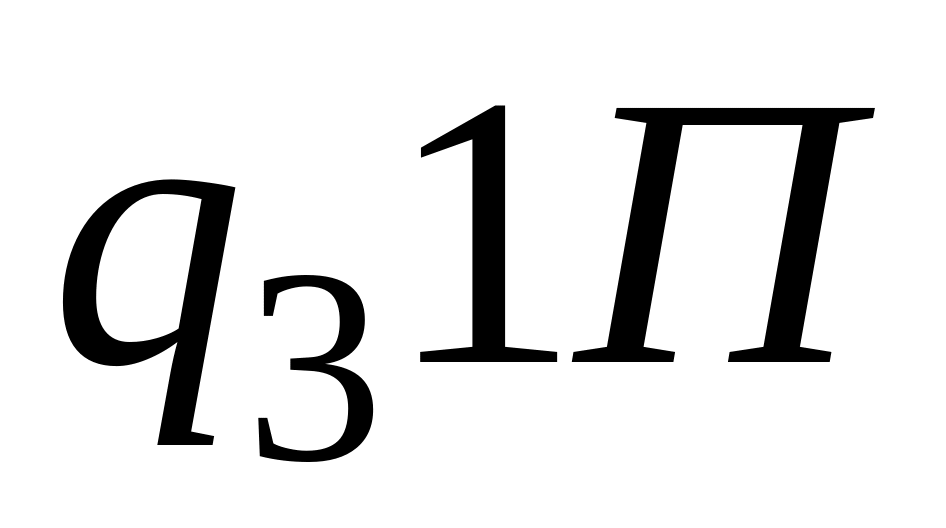
1