Получить скнф, а затем перейти к сднф
6.2.
Построим таблицу истинности:
x |
y |
z |
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
Выделим все наборы переменных, для которых функция принимает значение 1 и каждому набору поставить в соответствие дизъюнкцию переменных и их отрицаний. Рассматриваемая функция будет представлена конъюнкцией этих конъюнкций.
СКНФ:
Переход к СДНФ:
Получить мднф для формул
Квайн предложил алгоритм получения сокращенной ДНФ (СкДНФ) : если в совершенной ДНФ провести всевозможные операции неполного склеивания и поглощения, то получим форму, которая называется сокращенной ДНФ.
Минимальной формой (МДНФ) называется такая сокращенная форма, которая содержит наименьшее количество элементарных высказываний.
1.Получить СДНФ.
– ДНФ
– СДНФ
1 2 3 4 5 6
2. Операция склеивания
1-2 |
|
1-3 |
|
1-5 |
|
2-4 |
|
3-4 |
|
3-6 |
|
СкДНФ
– сокращенная ДНФ
3. Импликантная таблица
Строки – импликанты (конъюнкции сокращенной ДНФ)
Столбцы – конституенты (исходной совершенной ДНФ)
Отмечаем позиции матрицы на пересечении конституент (столбцов) и входящих в них простых импликант, которые перекрывают все конституенты (столбцы); выписываем данные наборы, соединяя импликанты знаками дизъюнкции.
-
+
+
+
+
+
+
+
+
+
+
+
+
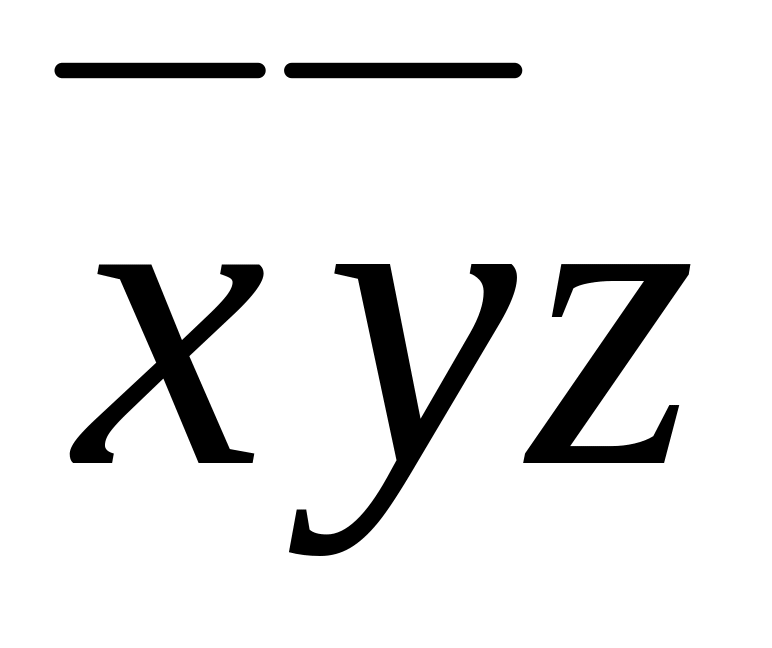
Выбираем импликанты, которые поглощают все кнституенты единицы.
Таким образом, получаем набор функций, называемых тупиковыми.
МДНФ1
=
МДНФ2
=
Выбирается тупиковая форма, содержащая минимальное количество переменных – она и будет являться минимальной ДНФ (МДНФ).
МДНФ =