
- •Ковалев а.Н. Эконометрика
- •Ковалев а.Н. Эконометрика
- •Методические рекомендации для проведения лабораторных занятий и самостоятельной работы студентов по курсу «Эконометрика» предназначено для студентов всех специальностей и направлений подготовки вуза.
- •Содержание
- •Введение
- •Тема 1. Предмет, метод и задачи эконометрики
- •Контрольные вопросы
- •Тема 2. Парная регрессия и корреляция
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Задача 6. В результате наблюдения 16 пар переменных (х и y) получены следующие данные:
- •Тема 3. Множественная регрессия и корреляция
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Тема 4. Нелинейные регрессионные модели
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Тема 5. Регрессионные модели с переменной структурой
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Тема 7. Системы одновременных уравнений
- •Контрольные вопросы
- •Задания для практических занятий и самостоятельного решения
- •Глоссарий
- •Словарь терминов
- •Примерная тематика рефератов
- •Список литературы
- •Ковалев Александр Николаевич Эконометрика
- •308023, Г. Белгород, ул. Садовая, 116а
Контрольные вопросы
Что такое «стационарный процесс»?
Какие гипотезы проверяются с помощью критерия Дарбина –Уотсона?
Какие параметрические тесты применяются для проверки постоянства дисперсии?
Какие непараметрические тесты применяются для проверки постоянства математического ожидания?
Каким образом нестационарный временной ряд можно преобразовать в стационарный?
Как осуществляется обратное преобразование стационарного ряда в нестационарный?
Что собой представляют модели авторегрессии?
Каким образом учитываются сезонные колебания в моделях временных рядов?
Задания для лабораторных занятий и самостоятельного решения
Задача 1. На основании следующих данных об обороте розничной торговли торгового предприятия обоснуйте выбор формы модели и постройте модель временного ряда:
(тыс. руб.)
Кварталы |
Годы |
|||
2008 |
2009 |
2010 |
2011 |
|
1 |
37,0 |
44,4 |
49,4 |
55,6 |
2 |
27,2 |
29,6 |
34,6 |
40,7 |
3 |
30,9 |
37,0 |
39,5 |
43,2 |
4 |
55,6 |
61,7 |
67,9 |
66,7 |
Задача 2. Используя представленные данные о величине выручки от реализации кооперативной организации обоснуйте форму модели и постройте модель временного ряда:
(тыс. руб.)
Кварталы |
Годы |
|||
2008 |
2009 |
2010 |
2011 |
|
1 |
1512 |
2100 |
1890 |
1344 |
2 |
1470 |
1932 |
1680 |
1218 |
3 |
1302 |
1680 |
1428 |
1008 |
4 |
1092 |
1260 |
1050 |
630 |
Дайте прогноз выручки от реализации на 1 и 2 кварталы 2012 года.
Задача 3. Используя представленные данные о динамике показателя обоснуйте выбор формы уравнения тренда:
t |
Yt |
t |
Yt |
1 |
120,2 |
11 |
201,9 |
2 |
126,6 |
12 |
210,3 |
3 |
144,1 |
13 |
233,3 |
4 |
152,0 |
14 |
264,5 |
5 |
155,4 |
15 |
269,5 |
6 |
176,3 |
16 |
299,8 |
7 |
172,0 |
17 |
388,3 |
8 |
165,4 |
18 |
375,3 |
9 |
178,4 |
19 |
401,1 |
10 |
184,6 |
20 |
413,6 |
Задача 4. На основании представленных данных об обороте розничной торговли постройте автокорреляционную функцию и автокоррелограмму:
|
2009 |
2010 |
2011 |
январь |
743 |
679 |
820 |
февраль |
720 |
640 |
758 |
март |
786 |
706 |
850 |
апрель |
805 |
721 |
860 |
май |
842 |
756 |
911 |
июнь |
866 |
794 |
913 |
июль |
888 |
804 |
932 |
август |
893 |
788 |
929 |
сентябрь |
820 |
757 |
869 |
октябрь |
842 |
760 |
897 |
ноябрь |
841 |
766 |
872 |
декабрь |
853 |
774 |
908 |
Задача 5. Имеются следующие данные о выручке от реализации и прибыли кооперативной организации, млн. руб.:
Годы |
2010 |
2011 |
||||||
Кварталы |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
Прибыль |
80,5 |
92 |
94 |
115 |
126,5 |
138 |
161 |
184 |
Выручка от реализации |
115 |
138 |
126,5 |
140 |
161 |
172,5 |
195,5 |
230 |
Постройте уравнение регрессии прибыли по выручке от реализации, используя для устранения тенденции метод отклонения от тренда, метод последовательных разностей и метод включения в модель фактора времени. Оцените наличие автокорреляции в остатках при использовании каждого метода с помощью критерия Дарбина-Уотсона.
Тесты
1. Коэффициент автокорреляции уровней временного ряда первого порядка рассчитывается по формуле:
а)
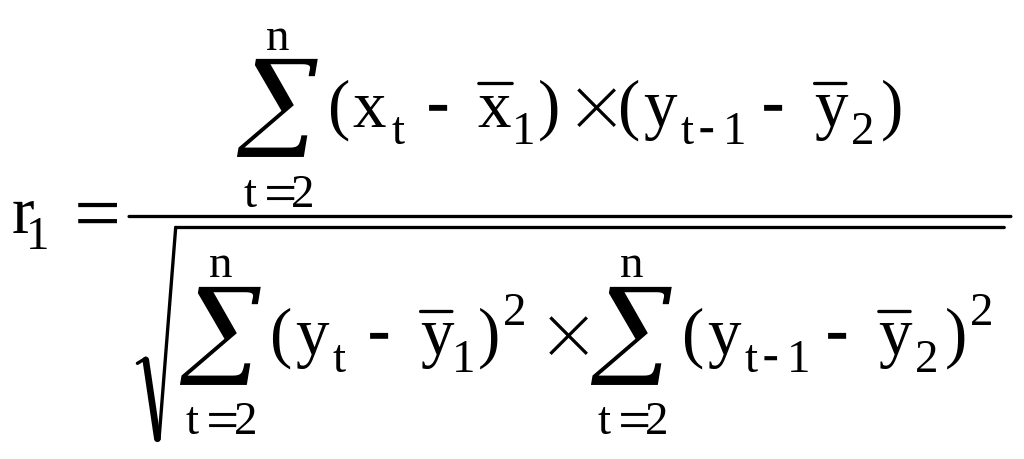 ;
;
б) ;
в)
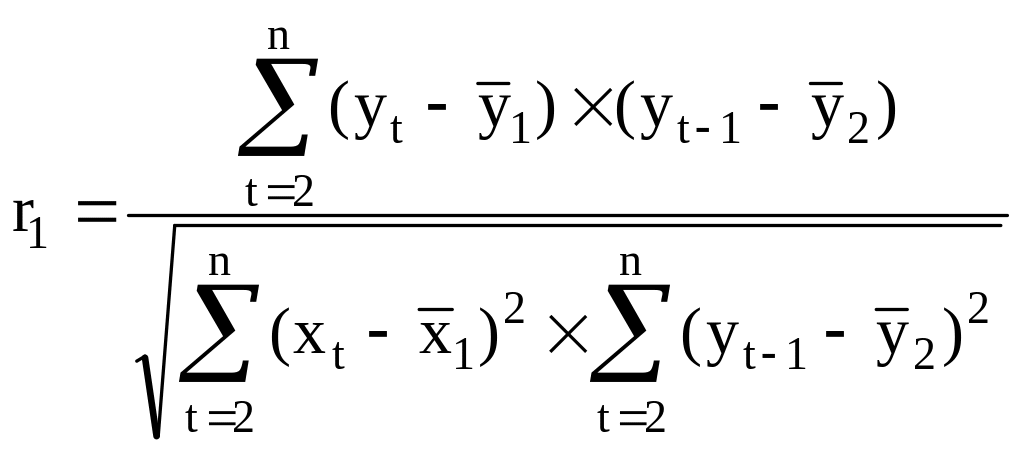 ;
;
г)
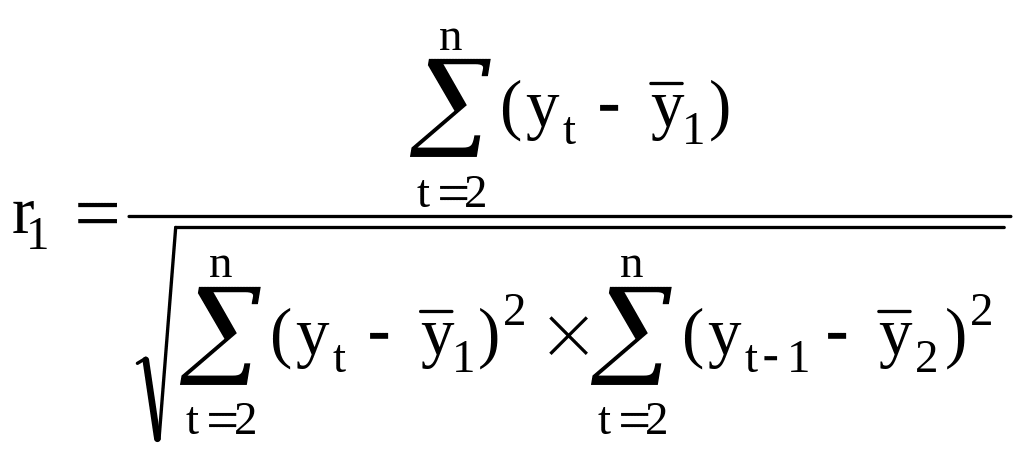 .
.
2. Величина d применяемая для оценки автокорреляции в остатках с помощью критерия Дарбина-Уотсона рассчитывается по формуле:
а)
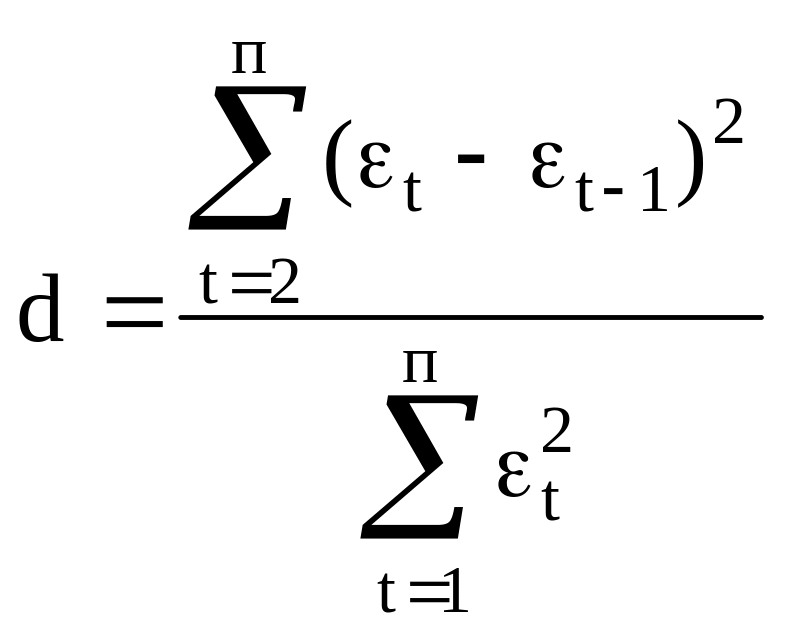 ;
б)
;
б)
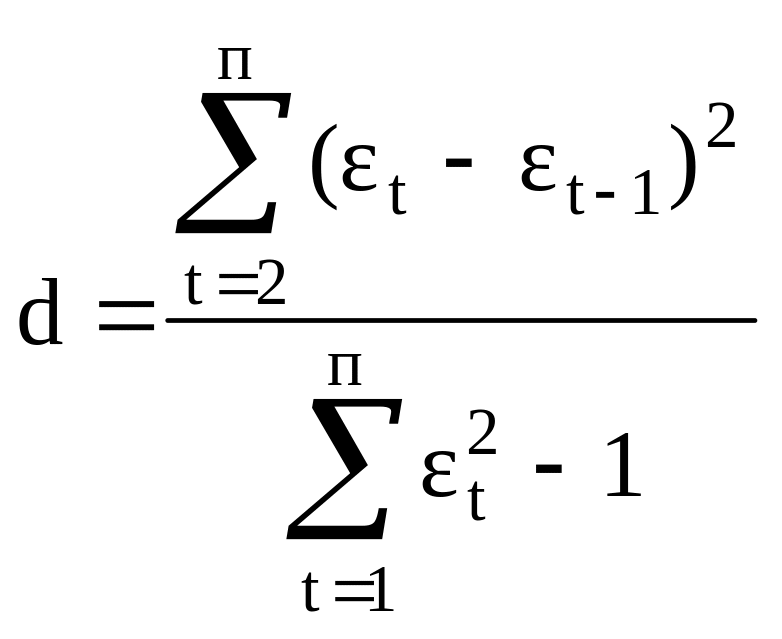 ;
;
в)
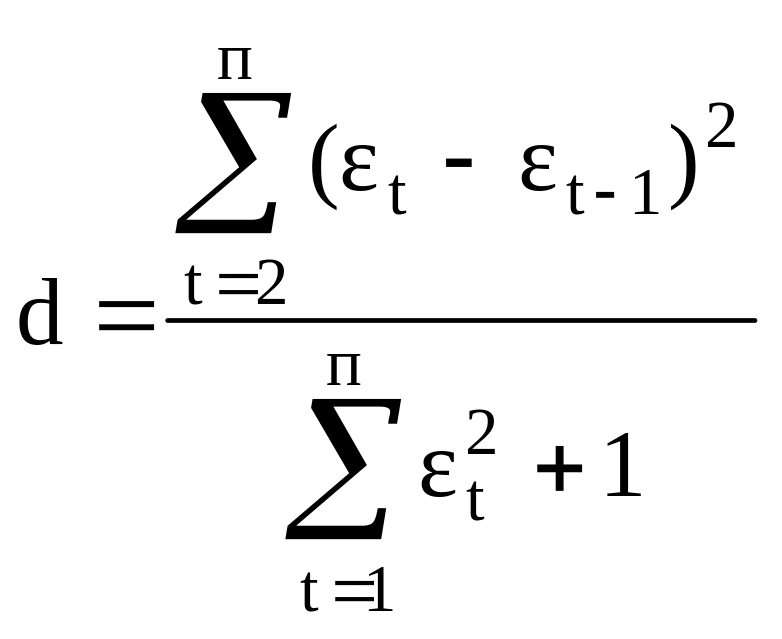 ;
г)
;
г)
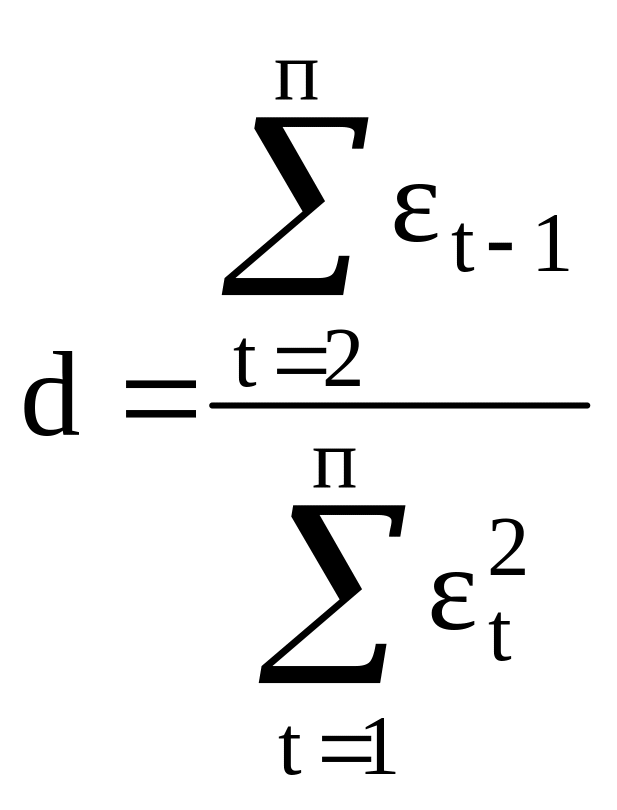 .
.
3. Временным рядом является совокупность данных:
а) характеризующих ряд объектов за один период времени;
б) характеризующих один объект за ряд последовательных периодов времени;
в) отражающих структуру экономических явлений
г) отражающих вариацию значений показателей
4. Стационарный временной ряд характеризуется:
а) постоянными по времени средним, дисперсией, и автокорреляциями;
б) малым количеством уровней ряда;
в) положительной тенденцией;
г) малой вариацией уровней ряда.
5. Автокорреляцией уровней ряда называют зависимость между:
а) фактическими и спрогнозированными уровнями ряда;
б) фактическими уровнями ряда и значениями случайной компоненты;
в) последовательными уровнями временного ряда;
г) значениями трендовой и циклической компонент.
6. Коррелограммой называют:
а) таблицу для расчета автокорреляции;
б) график зависимости автокорреляционной функции временного ряда от величины лага;
в) график зависимости уровней временного ряда от момента времени;
г) корреляционную матрицу.
7. В анализе временных рядов лагом называют:
а) количество уровней временного ряда;
б) число периодов, по которым рассчитывается коэффициент автокорреляции;
в) максимальное значение признака;
г) число спрогнозированных уровней.
8. Автокорреляционная функция временного ряда – это:
а) зависимость уровней ряда динамики от времени;
б) последовательность коэффициентов автокорреляции различных порядков;
в) зависимость фактических значений временного ряда от спрогнозированных;
г) последовательность положительных уровней временного ряда.
9. Авторегрессия - это:
а) зависимость между эндогенной переменной и ее лаговыми значениями;
б) зависимость между экзогенной переменной и ее лаговыми значениями;
в) зависимость между экзогенной и эндогенной переменной;
г) зависимость между экзогенной и эндогенными переменными.
10. Исключите лишнюю компоненту из составляющих уровней временного ряда:
а) циклическая;
б) трендовая;
в) структурная;
г) случайная.
11. Автокорреляцию в остатках можно определить используя:
а) t-критерий Стьюдента;
б) F-критерий Фишера;
в) критерий Энгеля-Грангера;
г) критерий Дарбина-Уотсона.
12. Для уменьшения влияния выбросов можно использовать:
а) лог линейный анализ;
б) сглаживание методом скользящей средней;
в) прогнозирование значений временного ряда;
г) автокорреляцию в остатках.
13. В аддитивной модели временной ряд представлен как:
а) сумма трендовой, циклической и случайной компонент;
б) произведение трендовой, циклической и случайной компонент;
в) произведения случайной компоненты и суммы трендовой и циклической компонент;
г) произведения трендовой компоненты и суммы случайной и циклической компонент.
14. В мультипликативной модели временной ряд представлен как:
а) сумма трендовой, циклической и случайной компонент;
б) произведение трендовой, циклической и случайной компонент;
в) произведения случайной компоненты и суммы трендовой и циклической компонент;
г) произведения трендовой компоненты и суммы случайной и циклической компонент.
