
- •Ковалев а.Н. Эконометрика
- •Ковалев а.Н. Эконометрика
- •Методические рекомендации для проведения лабораторных занятий и самостоятельной работы студентов по курсу «Эконометрика» предназначено для студентов всех специальностей и направлений подготовки вуза.
- •Содержание
- •Введение
- •Тема 1. Предмет, метод и задачи эконометрики
- •Контрольные вопросы
- •Тема 2. Парная регрессия и корреляция
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Задача 6. В результате наблюдения 16 пар переменных (х и y) получены следующие данные:
- •Тема 3. Множественная регрессия и корреляция
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Тема 4. Нелинейные регрессионные модели
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Тема 5. Регрессионные модели с переменной структурой
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Тема 7. Системы одновременных уравнений
- •Контрольные вопросы
- •Задания для практических занятий и самостоятельного решения
- •Глоссарий
- •Словарь терминов
- •Примерная тематика рефератов
- •Список литературы
- •Ковалев Александр Николаевич Эконометрика
- •308023, Г. Белгород, ул. Садовая, 116а
Задача 6. В результате наблюдения 16 пар переменных (х и y) получены следующие данные:
![]()
![]()
![]()
![]()
![]()
Постройте уравнение парной линейной регрессии.
Задача 7. На основании обследования 20 семей было установлено, что коэффициент корреляции между доходами и потреблением равен 0,85. Оцените статистическую значимость уравнения регрессии построенного по этим данным с помощью F-критерия Фишера.
Задача 8. По данным обследования 30 предприятий потребительской кооперации получены следующие характеристики распределения двух переменных (объема выпуска продукции и численности работников):
Коэффициент регрессии 0,5
Общая дисперсия результативного признака 81
Общая дисперсия факторного признака 262
Оцените тесноту связи между данными переменными с помощью коэффициента корреляции и определите коэффициент ковариации.
Задача 9. По данным корреляционной таблицы составить уравнение линейной регрессии Y на X и при уровне значимости 0,05 проверить гипотезу о равенстве нулю коэффициента корреляции.
у |
17 |
22 |
27 |
32 |
37 |
ny |
15 |
4 |
6 |
|
|
|
10 |
20 |
|
7 |
9 |
|
|
16 |
25 |
|
8 |
36 |
8 |
|
52 |
30 |
|
|
5 |
10 |
7 |
22 |
nx |
4 |
21 |
50 |
18 |
7 |
=100 |
Задача 10. Имеется фактические и теоретические данные объема заготовок организаций потребительской кооперации (млн. руб.):
№ |
Y |
YХ |
1 |
19,6 |
20,8 |
2 |
20,5 |
21,1 |
3 |
23,2 |
21,3 |
4 |
23,9 |
22,2 |
5 |
23,4 |
21,6 |
6 |
23,8 |
23,8 |
7 |
27,8 |
25,1 |
8 |
29,5 |
26,4 |
9 |
30,4 |
27,9 |
10 |
32,6 |
29,7 |
11 |
32,9 |
33,0 |
12 |
30,5 |
33,6 |
13 |
32,0 |
35,5 |
14 |
32,3 |
37,8 |
15 |
33,5 |
43,8 |
Оцените качество построенной модели с помощью коэффициента аппроксимации.
Задача 11. При исследовании корреляционной зависимости между ценой на нефть X и котировками акций нефтяных компаний Y получены следующие данные:
![]()
![]()
![]()
![]() Cov(X,У)=40
Cov(X,У)=40
Необходимо:
1) составить уравнение регрессии У по X;
2) используя уравнение регрессии, найти среднее значение котировки акций при цене на нефть 16,5 ден. ед.
Тесты
1. Коэффициент при факторной переменной в уравнении парной регрессии рассчитывается по формуле:
а)
![]() ;
;
б)
![]() ;
;
в) a0=y / x;
г)
![]() .
.
2. Линейный коэффициент парной корреляции рассчитывается по формуле:
а)
![]() ;
;
б)
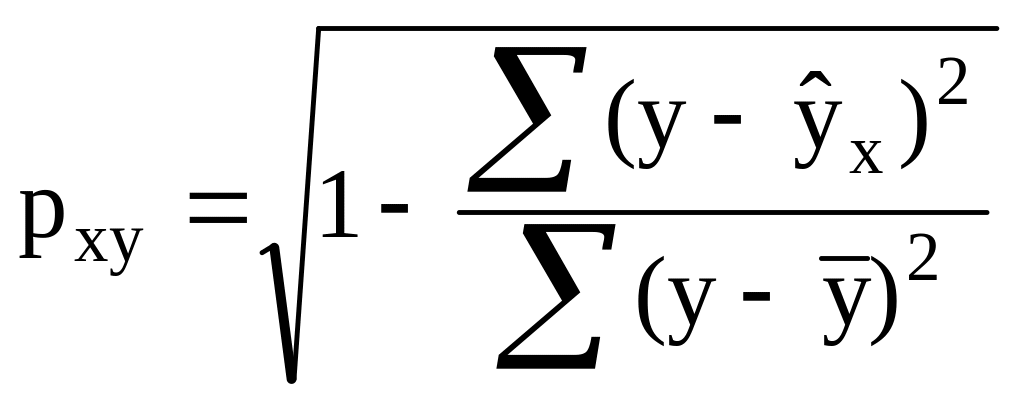 ;
;
в)
![]() ;
;
г)
![]() .
.
3. Средний коэффициент эластичности результативного признака в линейной парной регрессионной модели рассчитывается по формуле:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
4. Возмущением называют:
а) фактическое значение результативного признака;
б) теоретическое значение результативного признака;
в) случайную величину, характеризующую отклонение реального значения результативного признака от фактического;
г) фактическое значение объясняющей переменной.
5. Коэффициент детерминации в модели парной линейной регрессии рассчитывается по формуле:
а)
![]() ;
б)
;
;
б)
;
в) ; г) .
6. Коэффициент регрессии показывает:
а) среднее изменение результата при изменении фактора на единицу;
б) среднее изменение фактора при изменении результата на единицу;
в) среднее изменение результата при изменении фактора на один процент;
г) среднее процентное изменение результата при изменении фактора на единицу.
7. Средняя ошибка аппроксимации модели парной линейной регрессии рассчитывается по формуле:
а) ; б) ;
в) ; г) .
8. При каких условиях относительное изменение результата будет происходить медленнее, чем изменение фактора:
а) а>0;
б) а = 0;
в) а<0;
г) а = -10.
9. Значение F-критерия Фишера для уравнения парной линейной регрессии рассчитывается по формуле:
а)
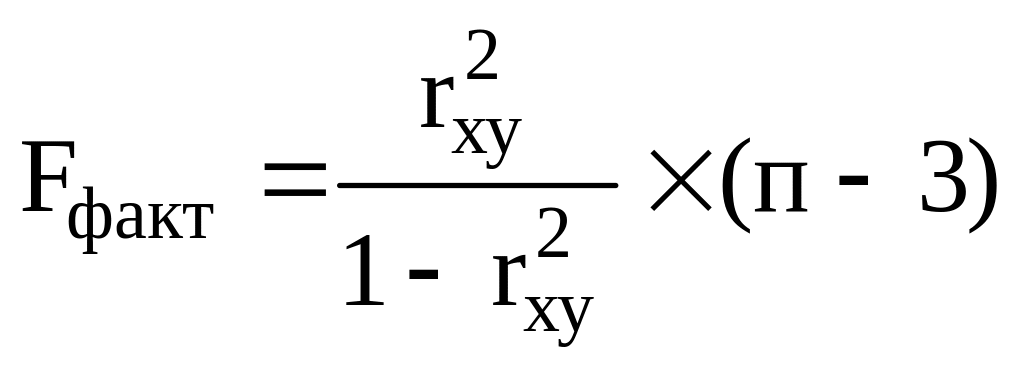 ;
б)
;
б)
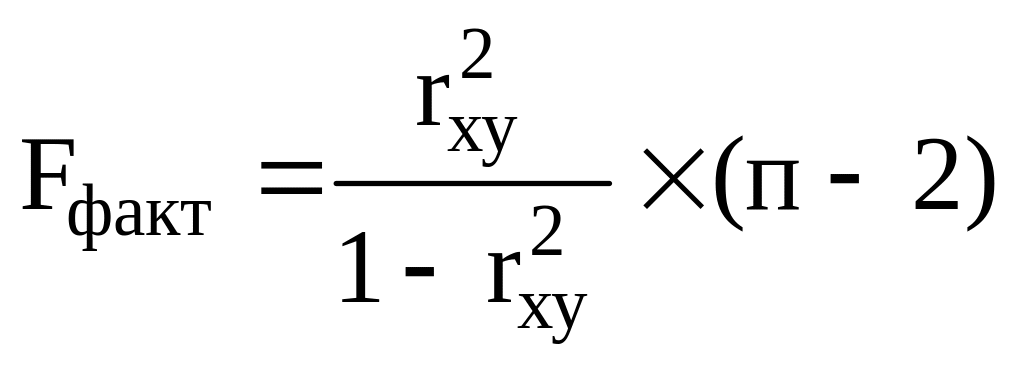 ;
;
в)
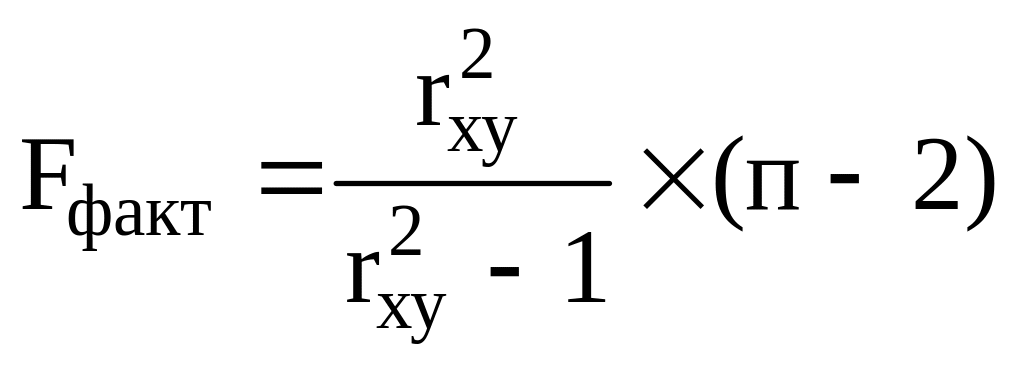 ;
г)
;
г)
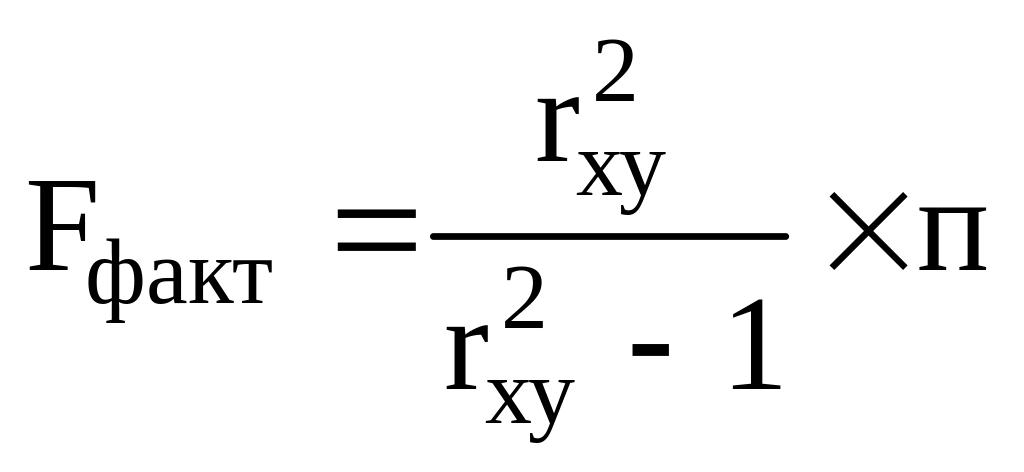 .
.
10. Для оценки качества подбора аппроксимирующей функции используется:
а) коэффициент корреляции;
б) коэффициент ковариации;
в) коэффициент детерминации;
г) среднее значение результативного признака.
11. Средняя ошибка коэффициента корреляции в модели парной линейной регрессии рассчитывается по формуле:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
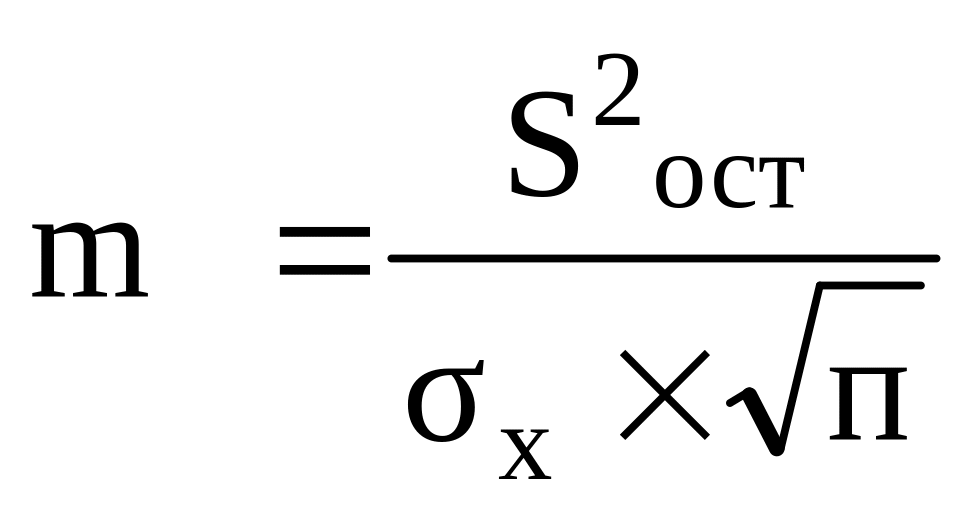 .
.
12. Оценка качества уравнения регрессии в целом проводиться с помощью:
а) t-критерия Стьюдента;
б) F-критерия Фишера;
в) критерия Энгеля-Грангера;
г) критерия Дарбина-Уотсона.
13. Средняя ошибка коэффициента свободного параметра в модели парной линейной регрессии рассчитывается по формуле:
а) ; б) ;
в) ; г) .
14. Оценка существенности параметров уравнения регрессии проводиться с помощью:
а) t-критерия Стьюдента;
б) F-критерия Фишера;
в) критерия Энгеля-Грангера;
г) критерия Дарбина-Уотсона.
15. Значение t-критерия Стьюдента для коэффициента корреляции модели парной линейной регрессии рассчитывается по формуле:
а)
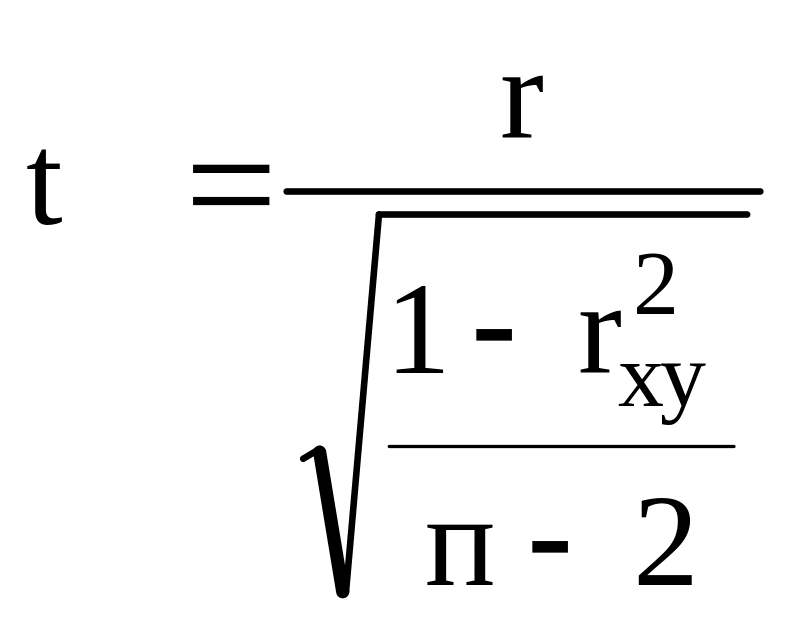 ;
б)
;
б)
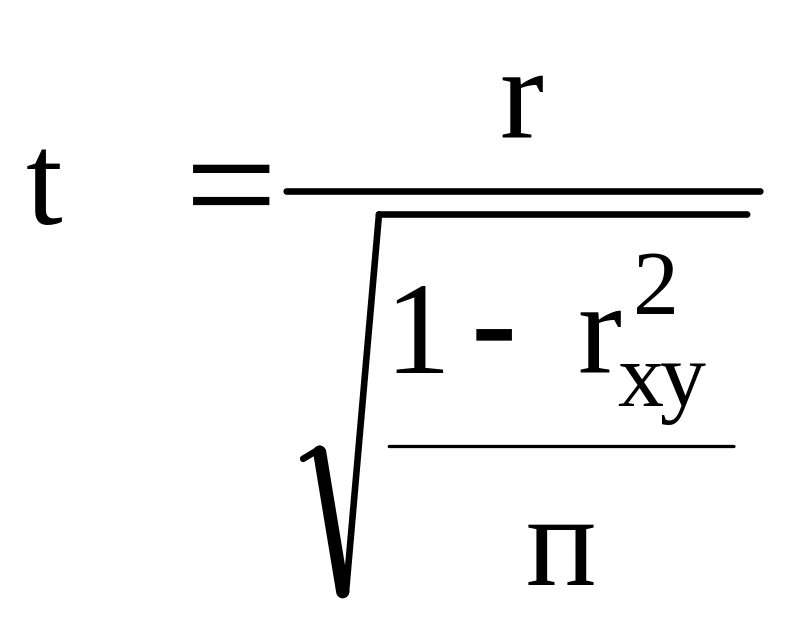 ;
;
в)
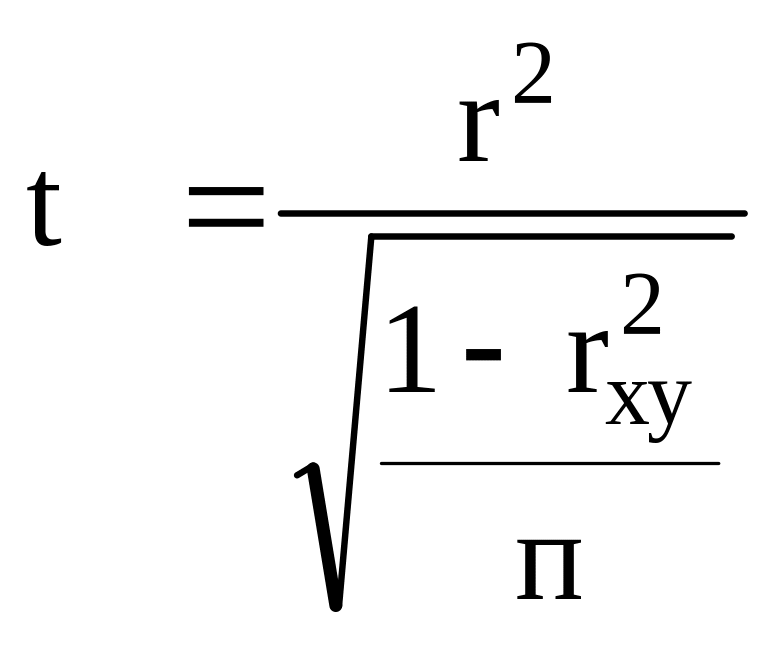 ;
г)
;
г)
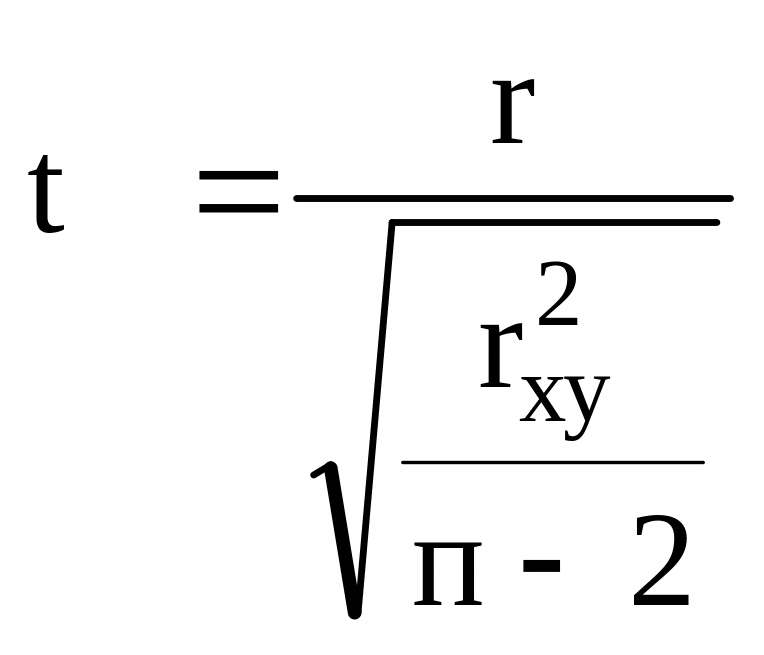 .
.
16. При применении МНК для оценки параметров уравнения регрессии:
а) сумма квадратов отклонений фактических значений результативного признака от теоретических минимальна;
б) сумма отклонений фактических значений результативного признака от теоретических минимальна;
в) сумма квадратов отклонений фактических значений результативного признака от теоретических максимальна;
г) сумма квадратов отклонений фактических значений результативного признака от теоретических равна нулю.
17. При функциональной зависимости:
а) каждому значению одной переменной соответствует определенное значение другой
б) каждому значению одной переменной соответствует определенное распределение другой переменной
в) множеству значений одной переменной соответствует неопределенное множество значений другой переменной
г) зависимость между переменными отсутствует
19. Значение t-критерия Стьюдента для коэффициента b при независимой переменной модели парной линейной регрессии рассчитывается по формуле:
а)
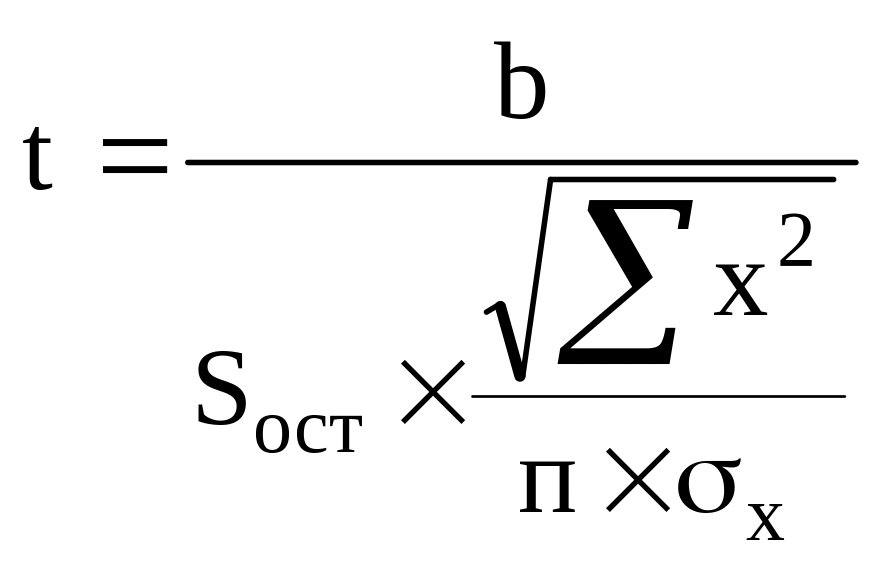 ;
б)
;
б)
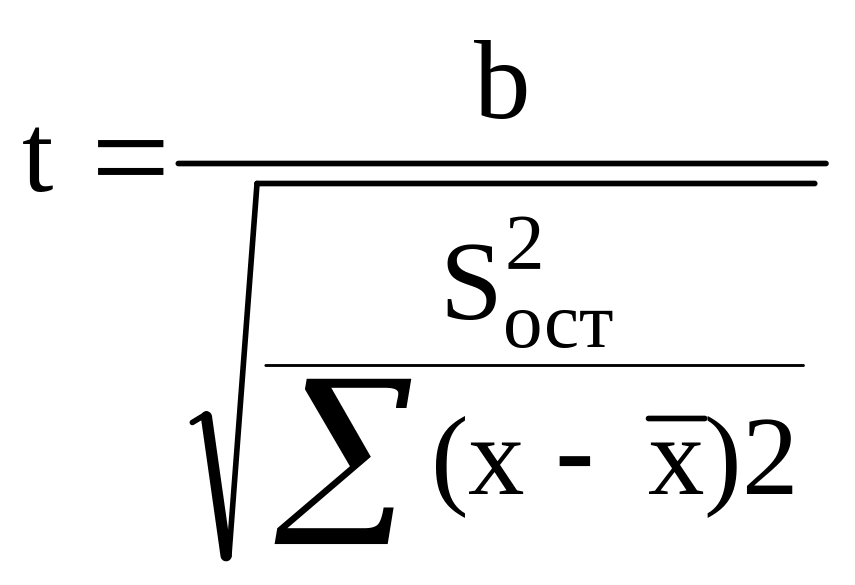 ;
;
в)
![]() ;
г)
;
г)
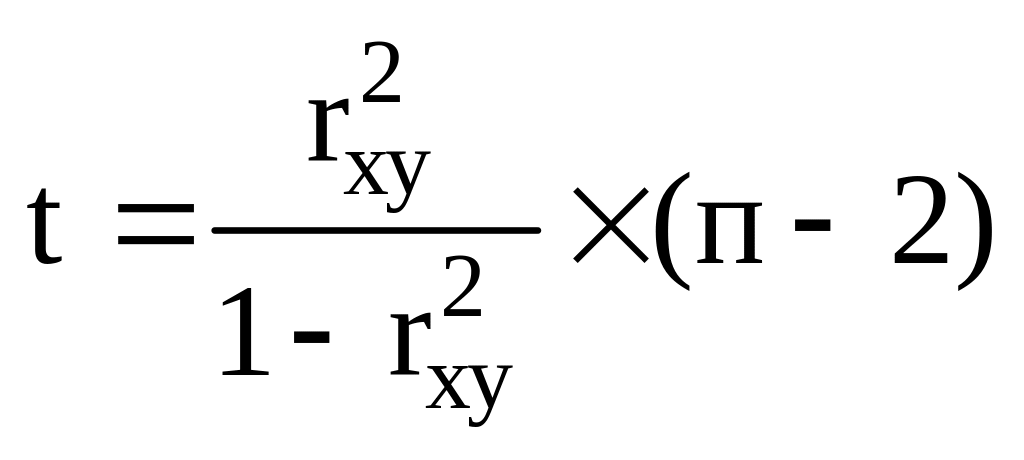 .
.
18. При какой зависимости каждому значению одной переменной соответствует определенное значение другой переменной
а) при функциональной;
б) при стохастической;
в) при статистической;
г) при вероятностной.
19. Проверить значимость уравнения парной регрессии значит:
а) определить значения параметров регрессии;
б) определить тесноту связи между переменными;
в) установить, соответствует ли математическая модель зависимости экспериментальным данным;
г) Проверить предпосылки применения МНК.
20. Качество модели в целом оценивает:
а) средние коэффициенты эластичности;
б) частные коэффициенты эластичности;
в) коэффициент множественной детерминации;
г) знак коэффициентов регрессии.
21.
Коэффициент эластичности для функции
![]() равен:
равен:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.

 х
х