21.Жұлдыздардың ішкі құрылысының теңдеулері, диффузиялық жуықтаудағы энергияны тасымалдау теңдеуін талқылыаңыз.

Жұлдыздардың ішкі құрылысын эксперименттен анықталатын жұлдыздардың сыртқы сипаттамалары негізінде жұлдыздық құрылым теңдеулер (жұлдыздардың ішкі құрылысының теңдеулері) көмегімен есептеуге болады. Бұл теңдеулер мыналар.

1. Гидростатикалық тепе-теңдік теңдеуі:

=- p P = Pgas + Prad

2. Масса теңдеуі:

=4π p немесе = ρdr

3. Диффузиялық жуықтаудағы энергияны тасымалдау теңдеуі:

= -4π D

мұндағы - =a сәулелі энергияның тығыздығы, D=cl/3=c/(3kρ) оның диффузия коэффициенті. Бұл теңдеуді былай жазуға болады

=-

Бұл теңдеулер тек сәулелі жылу тасымалдау үшін жарамды. Конвекциялық тасымалдау аймағында изэнтропиялық шартты қолдану қажет: (dS/dr=0) температура арқылы ол былай жазылады:

=(1- )

4. Энергия балансының теңдеуі (ол ядродағы энергия бөлінуін

өрнектейді):

=4π ρ ℰ

мұндағы ℰ(r) [эрг/(с*г)] – Күн центрінен r қашықтықта болатын T мен ρ

мәндері үшін массасы бірлік элементтегі энергия бӛліну жылдамдығы.

Бұл дифференциал теңдеулерді күй теңдеуімен:

= , =

Мөлдірсіздік пен энергия бөліну жылдамдығы үшін өрнектермен:

k=k(ρ,T,X,Y,Z)

ℰ=ℰ (ρ,T,X,Y,Z)

және шекаралық шарттармен

толықтыру қажет. X,Y,Z шамалар – элементтердің салмақтық үлестері: сутегінің (X ),гелийдің (Y) және басқалардың (Z ), μ - күн затының молекулалық салмағы.Мысалы, толығымен иондалған плазма үшін μ = 1/(2X + (3/4)Y + (1/2)Z); Күн үшін X ≈ 0.75, Y ≈ 0.23, Z ≈ 0.02 и μ× ≈ 0.6 (сутегі мен гелий жартылай иондалған фотосфера мен ядролық реакциялар нәтижесінде химиялық құрам өзгерген ядродан басқа қабаттар үшін). Суретте мысал үшін Күннің стандартты моделі үшін ρ(r), M(r), L(r) және T(r) үлестірілуі келтірілген. Күннің ішкі құрылымы мен оның параметрлері 2.2 2.3 суреттерде көрсетілген. Келтірілген мәндер жуықталған болып табылады, басқа әдебиетте кішкене өгеше мәндер де келтіріледі.

Көрінетіндей, Күн ішінде термоядролық реакциялар жүретін ядро, сәулелі

тасымалдау алқабы, конвекциялық аумақ және фотосфера, хромосфера мен

тәжден тұратын атмосфера айырылады.

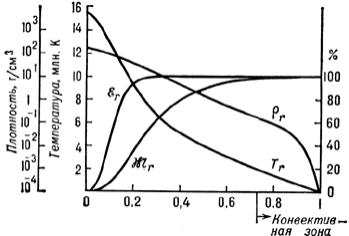
Сурет – Күнге тән массаның ( ) (Күннің толық массасынан пайыздар

түрінде),тығыздықтың (rr), температураныы (Tr) және сәулелену энергиясының ( ) (Күннің толық сәулелену энергиясына қатысты пайыздық

түрде). Горизонталь ось бойынша – күн радиуысына үлесі түріндегі Күн центрінен қашықтық.

22.Радиус-жарықтылық-масса тәуелділігін талқылаңыз.

lgR= lgL+2lg -мына өрнек маңызды 3 параметрді: радиус, жарықтылық және әсерлі (эффективті) температураны байланыстырады. Сонымен қатар, спектр және жарықтылық арасындағы тәуелділік (Герцшпрунг-Рэссел диаграммасы) бізге белгілі. Олай болса, өрнекке кіретін барлық шамалар өзара тәуелді және жұлдыздардың әрбір тізбегі үшін спектр-жарықтылық диаграммасында спектрлік класс пен радиус арасында белгілі бір заңдылықты табуға болады. Ол үшін спектр-жарықтылық диаграммасының түрін аздап өзгерту керек болады. Визуалды абсолют жұлдыздық шама орнына абсолют болометрлік жұлдыздық шаманы, ал спектрлік класс орнына – сәйкес әсерлі температураны егіземіз. Бұл жағдайда «ескі» диаграмманың жалпы сипаты негізінен сақталады. Соңғы сызылған диаграммада радиустары бірдей жұлдыздардың орны түзу сызықпен көрсетіледі, себебі Lg L және Lg Тэфф арасындағы тәуелділік – сызықты. Суретте тұрақты радиустарының сызықтары келтірілсе, бұл сызықтар бізге жұлдыздардың өлшемдерін олардың жарықтылығы ө және спектрі бойынша табуғаболады. Суреттен жұлдыздардың радиустары өте үлкен аралықтарда өзгеретінін көреміз, яғни жүздеген (мыңдаған) R - тан (алыптар және аса- алыптар) (102 - 103)R -қа (ақ ергежейлілер) дейін. Олай болса, жұлдыздық атмосфералардың температураларының (ерекшеліктері) айырмашылықтарды 10 есеге дейін ғана болса, ал диаметрлеріндегі өзгешелік дәрежесіне дейін жетеді. Суретте аса алыптардың тізбегі түзу сызықпен келтірілген. Бұл осы жұлдыздар үшін болометрлік жарықтылық пен радиус арасындағы эмпирикалық тәуелділікті анықтауға мүмкіндік береді. Мысалы, бас тізбектегі көптеген жұлдыздар үшін келесі өрнек пайдаланылады:

= .

Ал, маңызды шамалардың бірі – массаны дара жұлдыздар үшін анықтау өте қиын. Кейбір жағдайларда Кеплер заңы көмегімен қос жүйелердің компоненттерінің массаларын анықтауға болады. Сондықтан аздаған жұлдыздар тобы үшін массаны болометрлік масса мен болометрлік жарықтылық арасындағы байланыссыз табуға болады, ол 198–суретте келтірілген.Бұл суретте түзу = тәуелділігін көрсетеді, ол бас тізбектегі көптеген қосжүйелердің компоненттері үшін орындалады. (11.9) өрнектен бас тізбектің жоғарғы бөлігінде массалары Күн массасынан 10–даған есе көп ең ауыр жұлдыздар орналасқанын көреміз. Бас тізбекті жағалай төмен түскен сайын жұлдыздар массасы кеми түседі. Ергежейлілердің массасы Күннен аз. M < 0,02 M болған кезде заттан жұлдыз түзіле алмайды, ол планетаға сығымдалады. (11.9) өрнек берілген қалыпты жұлдыздар үшін әділ десек, онда массалары белгілі жұлдыздарды Герцшпрунг-Рэссел диаграммасында сала отырып массалары бірдей жұлдыздар үшін түзу сызуға болады. Сонымен, спектр-жарықтылық диаграммасын жұлдыздар күйінің диаграммасы деп қабылдауға болады.