
- •1.Метрология және оның тарихы.Метрологияның мақсаттары.
- •2)Өлшеу жəне оның түрлері. Өлшеуді класификациялау
- •3 Өлшеудің тұтастығын қамтамасыз етудің техникалық негіздері.
- •4 .Прибор шкаласын градуирлеу. Өлшеу құралдарын градуирлеу. Термоқосақ, оны градиурлеу.
- •Өлшеу нəтижелерін графиктік əдіспен өңдеу.
- •6 Берілген шаманың шкаласы(өлшеудің шкаласы). Негізгі реперлер жəне негізгі интервалдар. Фаренгейт шкаласы. Цельсий шкаласы.
- •Физикалық шамалардың өлшем бірліктері. Бірліктер жүйесі. Негізгі бірліктер.Бірліктер жүйесін құрудың негізгі принципі. Мөлшердің метрлік жүйесі. К.Гаусстың «Абсолют бірліктер жүйесі».
- •Халықаралық бірліктер (си) жүйесі жəне оның артықшылықтары
- •Өлшеу құралдары жəне оның түрлері. Өлшеу приборының принципиальді жəне құрылымдық схемалары.
- •10 Жүйелік қателіктер.
- •11 Гаусс таралуы жəне оның негізгі сипаттамалары. Математикалық
- •12 Тікелей өлшеу нəтижелерін математикалық өңдеу. Орташа
- •Өлшеу нəтижелеріне түзету енгізу.
- •16 Ағаттықты алып тастау.
- •18 Си жүйесіндегі когерентті туынды бірліктердің жасалуының
- •20 Нәтижелерді дөңгелектеу ережесі. Мәнді цифрлар. Нәтижелерді дұрыс жазу.
- •21. Си бірліктерімен тең қолданылатын бірліктер
- •22Кездейсоқ қателіктер ұғымы. Кездейсоқ қателіктердің байқалу ықтималдылықтарының таралуы.
- •23 Ең кіші квадраттық әдіс.
- •24 . Қазақстанның эталондық базасы Эталондар-бірліктің размерін өлшеу құралдарына беру мақсатында оны сақтап және қайта жаңғырта алатын өлшеу құралдары.
- •25 Си жүйесінің бірліктері және олардың анықтамалары.
- •26 . Физикалық шамалар арасындағы байланыс теңдеуі.
- •27Физикалық шама. Физикалық шаманың сипаттамалары. Негізгі және туынды шамалар.
- •28.Си Халықаралық бірліктер жүйесі, оның кезінде ссСр-ға кіргізілу тарихи этаптары
- •29 Халықаралық, мемлекетаралық және ұлттық эталондар
- •30.Өлшеудің негізгі теңдеуін қорыту.
- •31.Метрологияның аксиомалары(постулаттары).
- •32. Гауус функциясының қасиеттері.
- •33.Өлшеу. Өлшеудің құрылымдық элементтері.
- •34.Өлшеу нəтижесінің сапасы.
- •36.Жанама өлшеу нəтижелерін математикалық өңдеу.
- •37.Метрологияның нысандары. Олардың анықтамалары. Метрологияға қатысты негізгі ұғымдар.
- •39.Өлшемділік.Өлшемділіктің теңдеуін қорытып шығару.
- •Өлшеу əдістерінің класификациясы.
- •Өлшемділікке анализ.
- •42 Си жүйесінің негізгі жəне қосымша бірліктерінің анықтамалары.
- •43 Өлшеудің тұтастығын қамтамасыз ету. Метрологияға қатысты негізгі ұғымдар (анықтамаларын беру керек).
- •Кездесоқ оқиғалар мен шамалардың (қателіктердің) байкалу ықтималдықтарының таралу заңдылықтары: Бірқалыпты таралу, үшбұрышты таралу заңы, трапециялық таралу заңы.
- •Жүйеден тыс өлшем бірліктері. Еселік жəне үлестік бірліктер. Уақытша қолданылатын бірліктер.
- •46 Түзусызықты функцияның параметрлерін «ең кіші квадраттың əдіспен» есептеу.
- •Цельсий шкаласынан Фаренгейт шкаласына өту.
- •49 Фаренгейт шкаласынан Цельсий шкаласына өту.
- •50 Сгс,мкс,мкгсс,мкса,мсс,мтс бірліктер жүйелері.
- •52 Өлшеу құралдарының (өлшегіш прибор) метрологиялық сипаттамалары
20 Нәтижелерді дөңгелектеу ережесі. Мәнді цифрлар. Нәтижелерді дұрыс жазу.
Өлшеулерді орындай отырып олардың дәлдігі аспаптардың дәлдігіне жақындатуға ұмтылу керек. Өлшеулер нәтижелеріне математикалық өңдеу жасағанда, тура өлшеулердің дәлдігімен көрсетілген дәлдікке дейін есептеудің ешқандай мағынасы жоқ.сандарды дөңгелектеу ережесі

2)жуықтап алынған сандарды қосқанда немесе бір-бірінен алғанда қай санда ең аз ондық таңба бар, соншама ондық таңбасын нәтижеде сақтау керек

3)жуықтап алынған сандарды көбейткенде, бөлгенде, дәрежеге шығарғанда, түбір алғанда, логарифмдегенде нәтижесін осы сандардың үтірден кейінгі цифрлер (нөлден басқа цифрлер) саны ең аз сан бойынша алынады


4)кестелік
шамаларды дәл өлшенбеген шамадан бір
цифрге артық болатындай дөңгелектеу
керек. Сонымен қатар олардың қателіктерін
ескермеуге болады. Мысалы, дөңгелектің
 ,
,
 болсын.Диаметрді микрометрмен өлшегенде
болсын.Диаметрді микрометрмен өлшегенде
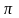 мынадай
нәтиже алынды: D=20,51
мм (төрт мәнді цифрлер). бұл жағдайда
бес мәнді цифрге дейін дөңгелектейді
(
).
Тәжірибе нәтижелерін дұрыс жазбау(жаңылыс
жазу). Мысалы, таразы басындағы таразы
тастарының мәндерін дұрыс есептемеу.
Тәжірибені жүргізуші адам прибордың
көрсеткіштерін екінші бір адамның айтуы
бойынша жазуы. Жаңылыс жазу, көбінесе,
6 және 9 цифрларын ауыстырып жазудан
кетеді, мысалы, 369 орнына 396 деп жазады.
мынадай
нәтиже алынды: D=20,51
мм (төрт мәнді цифрлер). бұл жағдайда
бес мәнді цифрге дейін дөңгелектейді
(
).
Тәжірибе нәтижелерін дұрыс жазбау(жаңылыс
жазу). Мысалы, таразы басындағы таразы
тастарының мәндерін дұрыс есептемеу.
Тәжірибені жүргізуші адам прибордың
көрсеткіштерін екінші бір адамның айтуы
бойынша жазуы. Жаңылыс жазу, көбінесе,
6 және 9 цифрларын ауыстырып жазудан
кетеді, мысалы, 369 орнына 396 деп жазады.
21. Си бірліктерімен тең қолданылатын бірліктер
Си бірліктерімен қатар қолданатын бірліктер, минут, тәулік, тонна, литр, сағат, градус, гектар, процент, промилля, децибел т.б Өлшем бірліктердің Халықаралық жүйесі (Си жүйесі) өлшемдердің халықаралық қалпы, метрлік жүйенің заманауи нұсқасы. Си күнделікті өмірмен қатар ғылым мен техникада әлемде ең көп пайдаланылатын бірліктер жүйесі болып табылады.Си жүйесі мына өлшемдерге негізделген. Ұзындық- метр, масса- килограмм, уақыт- секунд, температура- кельвин, ток күші- ампер, жарық күші- кандела, зат мөлшері- моль.Халықаралық бірліктер жүйесінің мынадай артықшылықтары бар:
Әмбебаптығы -ғылым мен техниканың, өндірістің барлық аумақтарын қамтиды.
Бірліктердің унификациялануы. Мысалы, бұрын қолданылып келген қысымның бірнеше бірліктерінің (атм, ат, мм.сын.бағ, мм.су.бағ т.б) орнына Халықаралық жүйеде жалғыз паскаль ғана , ал жұмыс пен энергияның бұрынғы бірліктерінің(кг*с, эрг, кал, ккал, эв, кВт*сағ т.б) орнына тек бір ғана Джоуль қолданылатын болды.
Қолдануға ыңғайлылығы
Когеренттілігі. Туынды шамалардың бірліктерін анықтайтын физикалық теңдеулердегі пропорционалдық коэффициенттің өлшемсіз бірге тең болуы.
Массаның өлшем бірлігі мен күштің өлшем бірлігінің айырмашылығының айқындалуы.
Теңдеу мен формулаларды жазудың жеңілдеуі
22Кездейсоқ қателіктер ұғымы. Кездейсоқ қателіктердің байқалу ықтималдылықтарының таралуы.
Кездейсоқ қателіктер деп- бірнеше рет қайталап өлшеу кезінде кездейсоқ өзгеріп отыратын қателіктерді айтады. Кездейсоқ қателіктердің жалпы сипаттамасы оның байқалу ықтималдылығы.Байқалу ықтималдылығы деп кездейсоқ шаманың байқалуына орайлы болатын жағдайлардың санының болатын жағдайлардың жалпы санына қатынасын айтады:
Р(А)=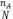
Байқалу ықтималдылығы математикалық статистика және ықтималдылық теориясына бағынады.
1. f(x)- ықтималдылықтың тығыздығы
2. х-бақыланатын шама
3.
а= =N(x)-математикалық
күтілу
=N(x)-математикалық
күтілу
4.
 -дисперсия
-дисперсия
5. б- орташа квадраттық ауытқу
f(x)=
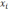 i=1,2,3,...,n
i=1,2,3,...,n
– a=Δ =Δ
Кездейсоқ қателік те Гаус теоремасына бағынады.
Үздіксіз кездейсоқ шаманың математикалық күтілуі:
a= =
= =
=
dP(x)- кездейсоқ шаманың шексіз аз dx интервалында байқалу ықтималдылығы.
