10 Жүйелік қателіктер.

Жүйелі қателік – бір физикалық шаманы қайталап өлшеген кезде заңды түрде өзгеретін жəне тұрақты түрде қалатын өлшеу қателіктерін құрайды. Олардың өзгешелік белгісі, олар болжанған, анықталған жəне осының арқасында тиісті түзетуді енгізумен толығымен жойылуы мүмкін. Систематикалық қателікті эксперимент арқылы анықтауға болады. Ол үшін берілген нәтижені басқа әдіспен алынған өлшеулер нәтижесімен салыстыру керек. Өлшеу аспаптардың дәл еместігі нәтижесінде пайда болатың жүйелік қателікті құралдық қателік деп атайды. Таңдалған өлшеу әдісінің жетілмегендігі нәтижесінде пайда болатын жүйелік қателікті  әдіс қателік  деп атайды.

11 Гаусс таралуы жəне оның негізгі сипаттамалары. Математикалық

күтілу. Дисперсия. Орташа квадраттық ауытқу.

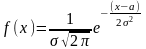
математикалық күтілу ең ықтимал мән

Дискретті кездейсоқ шамалар мәндері үздіксіз

М(х) х

Математикалық күтілу

Дискретті кездейсоқ шаманың математикалық күтілу деп шаманың барлық болатын мәндерінің олардың байқалу ықтималдығының көбейтінділерінің қосындысын айтыды.

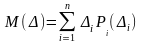
х мәндерінің математикалық күтілуден ауытқуы

Үздіксіз кездейсоқ шаманың математикалықкүтілуі кездейсоқ шама мен оның байқалу ықтималдығынан интеграл.

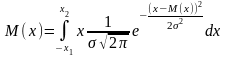
Дисперсия

Дискретті кездейсоқ шаманың дисперсиясы деп шаманың барлық болатын мәндерінің математикалық күтілуден ауытқуларының квадраттарының олардың байқалу ықтималдығына көбейтінділердің қосындысы.

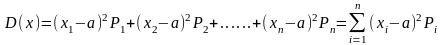
байқалу ықтималдығы

Үздіксіз кездейсоқ шаманың дисперциясы деп D(х) шаманың математикалық күтілуден ауытқуынан квадратының ықтималдыққа көбейтіндісінен интеграл

дисперция кездейсоқ шама мәндерінің математикалық күтілуге салыстырғандағы шашыраудың мөлшері.

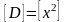
Дисперция ыңғайсыздығы дисперцияның өлшемділігінің квадратының өлшемділігіне байланыстылығы.

шашыраудың мөлшері

Орташа квадртаттық ауытқу

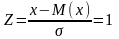
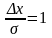
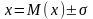
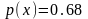
M(x)

0,68 немесе 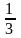сенімділікпен анықталған орташа квадраттық ауытқуды стандартты ауытқу деп атаймыз.

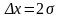
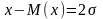
12 Тікелей өлшеу нəтижелерін математикалық өңдеу. Орташа

арифметикалық шама. Орташа квадраттық қателіктер. Сенімділік

ықтималдығы жəне сенімділік интервалы.

Тікелей өлшеулер – бұл ізделінді шаманы бірлік ретінде алынған шамамен тікелей салыстыру процесі. Тікелей өлшеу деп ізделініп отырған мәнді тәжәрибе барысында өлшеу құралының көмегімен бірден анықтауды айтамыз.Мысалы, ұзындықты штангенциркульмен, температураны – термометрмен өлшеу және т.б.Қателіктердің сипаттамаларын нүктелі және интервалды деп бөлу қабылданған. Нүктеліге кездейсоқ қателіктің ОКА-сы (СКО) мен жүйелі қателіктің модулінің жоғарғы шегі жатады, интервалдыға - өлшеу нәтижесінің анықталмаған шегі жатады. Егер осы шекаралар кейбір ықтималдылықтың жауабы ретінде анықталса, онда олар сенімді интервалдар деп аталады. Егер де қателіктің минималды мүмкін шегін, нақты жағдайда, сондай қателіктерді кездестіре алмасақ, онда олар шекті (шартсыз) интервалдар деп аталады.

Өлшеніп отырған шаманың ең ықтималды мәні оның орташа арифметикалық мәніне тең:

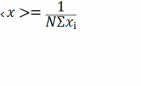
Әрбір жеке өлшеу нәтижесінің орта квадраттық қателігі деп мына өрнекті айтады:

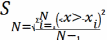
Сенімділік интервалын α және N –ге байланысты анықтайтын коэффициенттерді Стьюдент коэффициенттері деп атайды. Бұл коэффициенттер деп белгіленеді және арнаулы таблицалардан табылады.Сенімділік интервалын ∆х мына формуламен анықтаймыз:

∆х= *

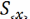
Мұндағы α – сенімділік ықтималдығы, α=0,95; -өлшеу саны.