2.1 Изоляция корней

Пусть функция непрерывна в области определения. Чтобы гарантированно существовало решение уравнения (1), функция должна быть знакопеременной в области определения. Процедура нахождения промежутка , внутри которого обязательно находится корень функции, называется, как уже отмечалось, этапом отделения корня или его изоляцией. Отделение корней может быть осуществлено численно или графически.

Численная процедура отделения корня, как правило, сводится к определению знака функции на некотором дискретном множестве значений аргумента. Чаще всего это множество представляет собой конечный набор равноотстоящих точек на оси абсцисс. При реализации этой процедуры руководствуются следующими правилами:

1. Если непрерывна на и , то существует хотя бы один корень .

2. Если непрерывна и монотонна на , причем , то корень единственный.

Следует отметить, что случаи, когда функция в отдельных точках принимает значения, равные нулю, а в остальных точках области определения сохраняет знак, этими правилами не отслеживаются.

Задачи

1. Найти промежутки изоляции корней уравнения .

Решение. Функция непрерывна и монотонна на всей области определения , т.к. , следовательно, уравнение имеет не более одного решения. Подбираем точки , такие, что .

. .

Ответ: [1; e].

2. Найти промежутки изоляции решения уравнений, используя графический метод: .

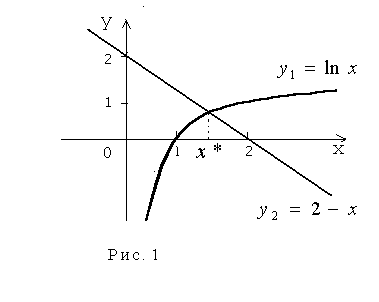
Решение. Запишем уравнение в виде и построим графики функций и . Абсциссы точек пересечения графиков ( ) равны корням функции . Из графика видно, что .

Проверка: . Ответ: .

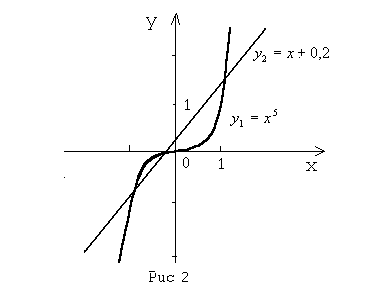
Запишем уравнение в виде и построим графики функций и . Как видно из графика, линии пересекаются в трех точках:

.

Проверка. .

. .

.

Ответ: .

Задачи для самостоятельного решения

Найти промежутки изоляции корней для следующих уравнений:

1). . 2). . 3).

Ответы: 1) [-1; 0]; 2) [-1; 0] и [1; 2]; 3) [1; 2].

2.2 Уточнение корней при помощи методов, не требующих вычисления производных

Пусть дано уравнение (1) и известно, что корень функции (решение уравнения) находится внутри : . Для уточнения корня с помощью итерационной процедуры строится, вообще говоря, бесконечная последовательность значений х . Если , то говорят, что итерационный процесс сходится к решению уравнения. Критерий прекращения расчетов обусловлен заданной точностью >0. Обычно применяют критерии:

или .

Скорость сходимости характеризует константа , такая, что . Если не зависит от , то сходимость линейная, если при , то сходимость сверхлинейная.

2.2.1 Метод деления отрезка пополам (метод бисекции)

Известно, что непрерывна на и имеет на этом промежутке единственный корень . Строим последовательность вложенных отрезков и принимаем середину каждого отрезка за . Расчеты производим по формулам: ;

затем для =1,2,3,....

;

; .

Критерий остановки расчетов: . Приближенное значение корня .

Скорость сходимости метода - линейная. На каждой итерации происходит уменьшение интервала неопределенности [a,b] в два раза. Нетрудно установить, что для того, чтобы исходный отрезок уменьшился не менее чем в  раз, необходимо осуществить [log₂]+1 итераций, где [g] означает целую часть числа g.

Метод половинного деления не обобщается на системы уравнений, относительно медленно сходится. Основное достоинство метода – он гарантированно сходится для любых непрерывных функций.