Для решения системы линейных уравнений
(1)
умножим
обе части уравнения на матрицу
,
получим эквивалентную (1) систему, матрица
которой
содержит нули в первом столбце ниже
главной диагонали. Затем умножаем обе
части уравнения на
и так далее:
.
В результате умножения матричного
уравнения (1) на цепочку матриц
приводим
А
к верхнему треугольному виду (для этого
потребуется
шагов). Перед выполнением k–го
шага матрица
имеет вид:
.
Поскольку
на k–ом
шаге обрабатывается только часть
матрицы, а именно элементы
,
,
,
то для экономии памяти ЭВМ можно на
каждом шаге уменьшать размерность
матрицы
и вектора
и строить матрицу отражения
размерности
.
Для удобства вычислений используют расширенную матрицу (Ab), где (n +1)-й столбец – это столбец свободных членов (см. п 4.1.1)
Для
k
= 0 считаем
(Ab).
Для
k
= 1 строим матрицу
,
где
(1;
0; ...; 0)T, 
– первый столбец матрицы
,
производим умножение
.
Затем
исключаем из
1–ю строку и 1–й столбец (получаем
размерности
).
Для
k
= 2 строим матрицу
,
где
(1; ...; 0)T,
– первый столбец матрицы
.
(Отметим, что размерность векторов
и
уменьшилась на единицу по сравнению с
размерностью векторов
и
)
Производим умножение
и вновь уменьшаем размерность
на единицу, исключая из нее 1–ю строку
и 1–й столбец.
Продолжаем
процесс для k
= 3, 4, ... Для
строим матрицу
размерности
,
и осуществляем последнее умножение:
.
В итоге получим систему с верхней
треугольной матрицей. Обратный ход
осуществляется так же, как в других
методах.
Задача
Решить систему из п.4.5.1 с использованием матриц отражения.
Решение. Прямой ход.
k
= 0.
(Ab)
=
.
k
= 1.
(1;0;0)Т;
(3;4;12)T;
;
(16;
4; 12); 
20,396;
(0,784;
0,196; 0,588).
Матрица
отражения: 
.
Результат первого шага:
.
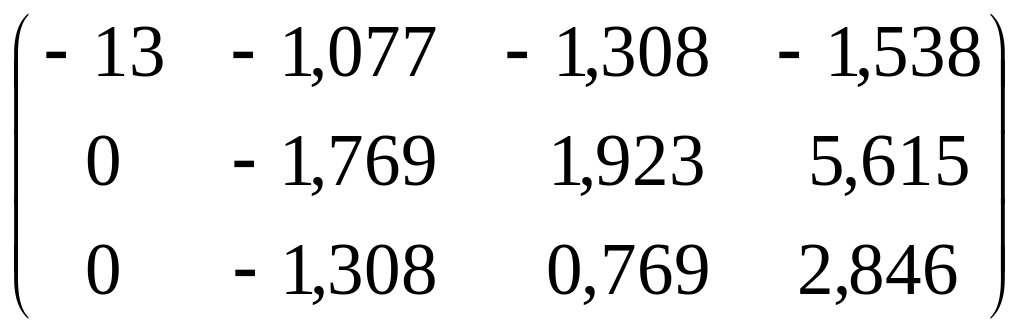Уменьшаем
размерность: 
.
k
= 2.
(1;
0)T;
(–1,769;
–1,308)T; 
2,200;
(–3,969;
–1,308);
4,179;
(–0,950;
–0,313);
.
Результат второго шага:
.
Результат прямого хода:
.
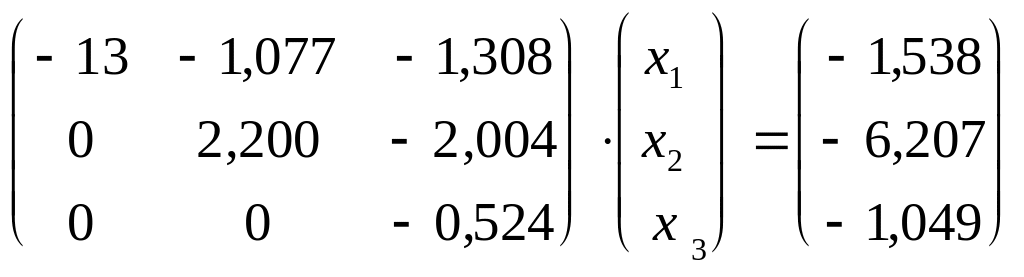Обратный ход:
; 
;
.
Ответ: ; ; .
Для контроля при построении матриц вращения и отражения можно проверять выполнение равенств, справедливых для всех ортогональных матриц : QTQ = E или QQT = E, где Е – единичная матрица.
Методы решения систем с использованием ортогональных преобразований обладают устойчивостью к ошибкам округления, легко программируются и нечувствительны к провалам главных миноров, в отличие от некоторых других схем (например, Гаусса). Однако, эти методы требуют большего числа арифметических операций (примерно вдвое больше).
Литература
[1], гл. III, работы №2, № 4–6.
[2], часть 1 гл. IV, §6, № 444–448, 450-451; §7, № 457.
[4], т. II, гл. VI, §2.1; §3.
[5], гл. II, §2.11.
[6], гл. III, §2,4,5,6.
[7], гл. V, §1.2, 1.5, 1.6.
Конспект лекций.
§5 Итерационные методы решения систем линейных алгебраических уравнений
Пусть требуется решить систему линейных алгебраических уравнений
,
(1)
где -квадратная невырожденная матрица.
Перепишем матричное уравнение (1) в виде
,
где,
например, матрица C
= E
– A
(в этом
случае
).
В
результате может быть организован
итерационный процесс, в ходе которого,
начиная с некоторого вектора
T
, строится последовательность
в соответствии с рекуррентной формулой:
,
0,
1, 2, ... .
Если
при этом существует предел
,
где
решение системы (1), то итерационный
процесс считают сходящимся.
В
отличие от прямых методов решение
системы с помощью итерационных методов
можно получить лишь с некоторой
погрешностью, которая обусловлена
критерием остановки расчетов. При этом
обычно используют норму вектора невязки
или норму разности
,
т.е., если требуется получить решение с
точностью
>0,
то расчеты выполняются до тех пор, пока
не будет выполнено одно из условий:
или
.
Итерационные
методы, как правило, легко программируются,
но иногда очень медленно сходятся или
даже расходятся (если не выполнены
условия сходимости). Для того, чтобы тот
или иной итерационный процесс сходился,
матрица
должна удовлетворять определенным
требованиям, а скорость сходимости
зависит от вида матрицы
.
Для ускорения сходимости можно
использовать итерационные методы с
числовым параметром
:
,
где параметр может выбираться на каждом шаге либо быть константой.