2. Граничні умови pec симетрії і авс

У рахунковому обсязі кожен вектор Е або Н обчислюється через 4 сусідніх вектора. Так відбувається по всьому об'єму. Але на кордонах самі останні вектори Е мають на гранях паралелепіпеда рахункового обсягу тільки три сусідніх вектора Н з чотирьох необхідних на ребрах - два. Тому точно обчислити поле Е на кордонах неможливо.

Проблема обчислення граничних полів вирішується різними способами.

1. Умови PEC - ідеальний провідник

Умови PEC такі, що граничні вектора Е ніколи не обчислюються, а, значить, завжди дорівнюють нулю. Як відомо, поле Е завжди дорівнює нулю в ідеальному провіднику, тому такі кордони ведуть себе як ідеальний провідник: електромагнітні хвилі 100% відбиваються назад в обрахункову область.

2. Умови симетрії

У деяких випадках поле Е або поле Н може бути симетричним щодо деякої площини. Тоді в цій площині можна задати умову симетрії і тим самим вдвічі зменшити рахунковий обсяг. При цьому поряд з даної площиною симетрії буде проходити кордон рахункового обсягу з умовами симетрії.

Симетрія може бути парній або непарній.

При непарній симетрії площину симетрії проходить всередині рахункового обсягу паралельно грані на відстані пів-осередку від грані. Умови непарній симетрії для симетрії по Е виходять простим перенесенням значень найближчих до кордону векторів Е на саму кордон, а для симетрії по Н виходять так само, але при цьому вектор Е змінює свій знак. Нижче наведені приклади непарній симетрії для Е і Н.

Умови парної симетрії дещо складніше. Площина симетрії проходить на відстані цілої осередку від кордону, тому окрім поля Е на кордоні необхідно пам'ятати про прилеглих до кордону векторах Н. При цьому симетрії по Е і Н відрізняються один від одного тільки знаками переносимих значень.

При парній симетрії граничні поля Е і Н встановлюються не одночасно, а на відповідних півкроку за часом.

3. Прості умови поглинання (АВС)

Для умов поглинання значення векторів електричного поля на кордоні обчислюються на підставі відомих полів у прикордонних шарах. Причому беруться прикордонні поля не тільки на поточному кроці по часу, але і на попередніх кроках. Всі ці умови намагаються спрогнозувати полі на кордоні.

У літературі зустрічається опис цілої низки простих умов поглинання різних авторів. Всього їх набереться з десяток. Практично найчастіше застосовують умови Мура (Mur) і Ліао (Liao). Решта не застосовують або використовують дуже рідко через їх більш низькій ефективності (Trefethen-Halpern, Higdon) або незручності у використанні (Retarded Time - RT), або через незастосовність в декартових координатах (Bayliss-Turkel), або через тенденції до втрати стабільності (відноситься майже до всіх умов, але особливо - до умов, заснованим на вищих порядках точності кінцевих різниць).

Всі умови мають досить низький коефіцієнт відбиття від кордону, що становить порядку 0,1 .. 1%, але тільки при падінні хвилі на межу під прямим кутом. При падінні під гострим кутом коефіцієнт відбиття зростає аж до 100% при падінні по дотичній. Через це кордону необхідно розташовувати якомога далі від джерела електромагнітних хвиль, щоб хвилі приходили до кордону під якомога більшими кутами, бажано по нормалі до кордону.

Слід зазначити, що оцінка ефективності тих чи інших простих граничних умов різна у різних авторів. Наприклад, одне джерело пише, що умови Ліао на 20 dB ефективніше умов Мура 2-го порядку. Інший пише, що умови Ліао на 12 dB гірше умов Мура 1-го порядку. Мається на увазі коефіцієнт відбиття. І обидва доводять свої висновки графіками порівняльних розрахунків.

Істина, швидше за все, посередині: для кожної конкретної задачі є свої оптимальні граничні умови. Одне погано - заздалегідь ніколи не знаєш, які краще.

Можливо, введення чисел подвійної точності радикально підвищить стабільність, але поки це недозволена розкіш, витрачає в два рази більше пам'яті і часу.

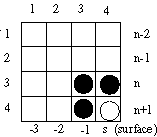
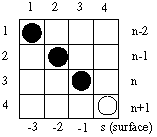
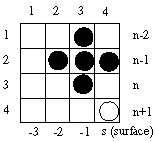
Отже, граничних умов багато. Тут розглянемо три варіанти найпростіших граничних умов: Мура 1-го порядку, Ліао 3-го порядку і RT. У таблиці S (велика) і s (мале) - різні змінні! S = (dT*c)/D - число Куранта, де D - крок за простором, dT-крок по часу, с-швидкість світла, а s - координата границі. s-1 - один осередок всередину рахункового обсягу, s-2 - два осередки від кордону і т.д. На пояснюючих малюнках від кордону (surface - зовнішньої поверхні рахункового обсягу) по горизонталі відкладена координата s, а по вертикалі - час у кроках рахунку (n - часовий індекс). Формула приведена в двох видах, що доповнюють один одного в просторі і часі. На малюнках порожній кружок - обчислюване значення, чорні кружки - необхідні значення. Відразу можна визначити, які змінні прикордонній області потрібно зберігати в додаткових масивах і скільки кроків по часу вони повинні зберігатися.

Таблиця 2.1 – Граничні умови

Умови	Формула	Пояснююча картинка
Mur 1-го порядку	En+1 (s) ≈En(s-1)+A1(En(s)-En+1(s-1)) A1≡(1-S)/(1+S) B(4,4) ≈B(3,3)+A1*(B(3,4)-B(4,3)) типово S = 0,5 для мінімального відбиття під прямим кутом, але може мінятися для отримання мінімального коефіцієнта відбиття під іншими кутами.
Liao 3-го порядку	En+1 (s) ≈En-2(s-3)+3(En(s-1)-En-1(s-2)) B(4,4) ≈B(1,1)+3*(B(3,3)-B(2,2)) Для даного випадку S = 0,5. Примітка: в літературі умови Ліао часто ставлять осібно з умовами ABC, тому вони базуються на інших вихідних передумовах.
RT-ABC	En+1 (s) ≈En-1(s-1)+5(En-1(s)-En-1(s-2))+(En(s-1)-En-2(s-1)) B(4,4)≈B(2,3)+5*(B(2,4)-B(2,2))+(B(3,3)-B(1,3)) Для даного випадку S = 0,5, крок за часом суворо півкроку по простору *, крок за простором суворо однаковий у всіх напрямках.

Видно, що найбільше масивів змінних потрібно зберігати для умов RT (5), найменше - для умов Мура (1). Для умов Ліао потрібно 3 додаткових масиву змінних.

2. Умови PМL

Примітка. Взагалі, дослівний переклад "Perfectly Matched Layer" виглядає як "ідеально узгоджений (поєднуваний) шар". Але, по-перше, по одному шару в цих граничних умовах не застосовують, а, по-друге, якщо один шар з чимось поєднується, то, безсумнівно, з іншим шаром. Тобто їх мінімум два, а значить, по-російськи, множина - "шари".

Умови PML вперше опубліковані в статті [J. P. Berenger, JOURNAL OF COMPUTATIONAL PHYSICS. 114, 185 (1994)], а потім отримали розвиток в публікаціях цього автора в 1995-1996 р. При виникненні інтересу до безумовно-стабільним алгоритмам були розроблені умови PML, адаптовані до нових алгоритмів.

Умови PML володіють низьким коефіцієнтом відображення (за деякими даними в мільйон разів менше, ніж у умов Мура), а також практичної незалежністю від кута падіння хвилі.

До недоліків умов PML слід віднести значно більший обсяг необхідної пам'яті, ніж для умов ABC і наявність нижньої граничної частоти, для зниження якої вимагається збільшення кількості шарів PML, а, отже, необхідної пам'яті. Як наслідок збільшення необхідного обсягу пам'яті відбуватися зниження швидкості обчислень.

За межами головного рахункового обсягу додаються додаткові осередки, навколишні рахунковий обсяг по периметру декількома шарами. Електричне і магнітне поле в цих осередках обчислюється майже так само, як і в рахунковому обсязі, але є відмінності.

По-перше, в рівняння в обов'язковому порядку вводяться електричні й магнітні втрати. У головному алгоритмі цих втрат може не бути взагалі. У рівняннях головного алгоритму, враховані тільки електричні втрати. Магнітні втрати вводяться так само, як і електричні, шляхом завдання "щільності магнітних струмів". Тоді рівняння Максвелла і виглядають так:

rot(H) = ∂D/∂t + J

rot(E) = - ∂B/∂t + J^* (2.9)

де:

D = ε ε_o E

J = σ E

B = μ μ_o H (2.10)

J^* = σ^* H

Відміна від (2.1) і (2.2) тільки в появі J * - щільності "магнітних струмів" і σ * - "магнітної провідності". З введенням магнітних втрат рівняння (2.9) стали симетричними.

По-друге, запроваджується поділ векторів і їх роздільне обчислення. Кожен вектор декартовій сітки Йі в межах PML ділиться на два паралельних вектора (дві компоненти). Сума цих векторів є повний вектор: Ex = Exy + Exz; Ey = Eyx + Eyz; Hz = Hzx + Hzy і т.д. Позначення розшифровуються так: Exy - вектор E в напрямку X, отриманий через сусідні вектори Hz, що лежать на прямій, паралельній осі Y. Зрозуміти це можна, подивившись на систему рівнянь Беренгера:

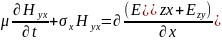
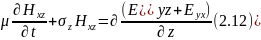
По-третє, теоретично, якщо виконується умова:

то на межі розділу двох середовищ швидкість електромагнітних хвиль не змінюється і відображення рано нулю. У той же час, оскільки σi і σi * не дорівнюють нулю, то відбувається поглинання електромагнітних хвиль в надрах PML.

На жаль, віддзеркалення все ж є:

- Від першого шару PML;

- Між шарами PML, оскільки для економії обчислювальних ресурсів втрати зростають від шару до шару (закон зміни втрат від першого шару до останнього називається "профілем втрат");

- Після останнього шару PML, оскільки там знаходиться PEC - межа.

Відображення від першого шару PML і між шарами PML викликано помилками звичайно-різницевої дискретизації, і, в першу чергу, тим, що вектори E і H (а, отже, σ_i та σ_i^* ) не збігаються в просторі. Для зниження відбиття усередині PML необхідно обмежувати швидкість росту втрат деяким розумною межею.

Беренгер показав, що при кожному конкретному значенні σ_i і σ_i^*, внаслідок цифрового відображення, відбувається відображення нормальних (перпендикулярних) до кордону електромагнітних хвиль, частота яких нижче fc (частота відсічення). Чим більше σ_i і σ_i^*, тим вище f_c. Тому при проникненні хвилі в межі PML спочатку йде відбиття від першого шару з провідністю σ₀ тих частот, які нижче fc0. Потім іде відображення від півшару з провідністю σ₀^* частот нижче f_c0^*. Причому f_c0 < f_c0^* . І так далі - все більш і більш високі частоти відображаються, причому відбиття від σ_i і від σ_i^*.

Відображення від PEC кордону після останнього шару PML відбувається зазвичай вже для вельми ослабленою хвилі. Відбита хвиля на зворотному шляху продовжує послаблюватися. Але якщо шарів мало (звичайно <5), то відбита хвиля може бути істотною.

Для зменшення відбиття від першого шару значення σ₁ спеціально вибирається маленьким. Для зменшення відбиття між шарами профіль втрат вибирається з обмеженою швидкістю зростання втрат. Для зменшення впливу хвилі, відбитої від РЕС кордону, збільшується кількість шарів PML.

Як варіант, Беренгер пропонує наступний геометричний профіль втрат:

де g - коефіцієнт геометричній прогресії; ∆x - крок по простору; с - швидкість світла; N - номер PML-шару, відраховуючи від інтерфейсу рахункового регіону і кордони; r - відстань від межі; R (0) - коефіцієнт відбиття від першого шару. Рекомендоване значення R (0) = 0.01 (1%) Коефіцієнт прогресії g рекомендується брати 2.15. Це значення отримано Беренгер експериментально, хоча зустрічаються й інші рекомендації.

σ^*(r) виходить через σ (r) з використанням (2.13).

На низьких частотах спостерігається різке збільшення коефіцієнта відбиття від границь PML. Нижня гранична частота відсічення для відомого значення електричної провідності на кордоні знаходиться з виразу:

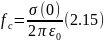
Для розрахунків відгуків від імпульсів - сходинок з постійної складової зворотна величина до (2.15) - 1/f_c - це максимальний час рахунку, при якому коефіцієнт відбиття від першого шару ще не перевищує заданого R (0).

Дискретизація рівнянь (2.11) та (2.12) відбувається так само, як і дискретизація рівнянь головного алгоритму. Для двох векторів Ex:

E_xyⁿ⁺¹_(i+1/2,j,k) = (1-0,5 σ_y()∆t)/ (1+0,5 σ_y()∆t) E_xyⁿ_(i+1/2,j,k) +

∆t/ (1+0,5 σ_y()∆t)/ ∆y (H_zx^n+1/2_{(i+1/2,j+1/2,k)} + H_zy^n+1/2_{(i+1/2,j+1/2,k)} -

H_zx^n+1/2_{(i+1/2,j-1/2,k)} - H_zy^n+1/2_{(i+1/2,j-1/2,k)}),

E_xzⁿ⁺¹_(i+1/2,j,k) = (1-0,5 σ_z()∆t)/ (1+0,5 σ_z()∆t) E_xzⁿ _(i+1/2,j,k) +

∆t/ (1+0,5 σ_z()∆t)/ ∆z (H_yx^n+1/2_{(i+1/2,j,k+1/2)} + H_yz^n+1/2 _{(i+1/2,j,k+1/2)} -

H_yx^n+1/2_{(i+1/2,j,k-1/2)} - H_yz^n+1/2_{(i+1/2,j,k-1/2)})

Для решти векторів Е все аналогічно. Для векторів Н рівняння аналогічні, але замість σ(r) береться σ^*(r).

H_xy^n+1/2_{(i,j+1/2,k+1/2)} = (1-0,5 σ^*_y()∆t)/ (1+0,5 σ^*_y()∆t) H_xy^n-1/2 _{(i,j+1/2,k+1/2)} -

∆t/ (1+0,5 σ^*_y()∆t)/ ∆y (E_zxⁿ _{(i,j+1,k+1/2)} + E_zyⁿ _{(i,j+1,k+1/2)} -

E_zxⁿ_(i,j,k+1/2) - E_zyⁿ_(i,j,k+1/2))

Як можна помітити, у рівняннях для векторів Е має суми типу (Hzx^{n +1/2}_{(i +1/2, j+1/2,k)} + Hzy^n+1/2_{(i+1/2, j+1/2, k)}). Це і є повний вектор, в даному випадку Hz. Коли обчислюється поле на кордоні рахункового обсягу, то з рахункового обсягу береться повний вектор Hz, а з граничного PML-шару - сума Hzx + Hzy. Також і для інших векторів.

На зовнішній межі PML, як уже говорилося, тангенціальні вектори Е дорівнюють нулю (PEC).

Профіль втрат залежить тільки від координати, що веде від інтерфейсу "рахунковий обсяг" - PML вглиб PML. На будь грані прямокутного рахункового обсягу вглиб PML веде тільки одна координата. Припустимо, це координата X. Тоді σ_x(r) змінюється по заданому закону, а σ_y(r) = σ_z (r) = 0. На ребрах вглиб PML ведуть уже дві координати (одна з σ дорівнює нулю), а в кутах вглиб ведуть всі три координати і, отже, змінюються всі σ (рис. 2.1).

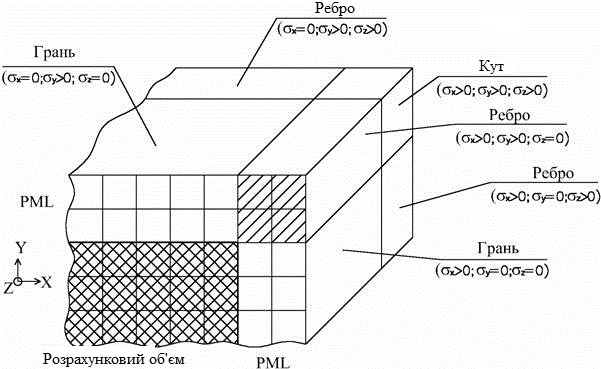
Рисунок 2.1 – Розрахунковий об’єм в оточені PML шарів