
- •1.Сызықты емес теңдеулерді шешудің сандық әдістері
- •2.Сандық интегралдау есебі
- •3. Сызықты емес теңдеулерді шешудің сандық әдістері
- •10.Функцияны интерполяциялау
- •12.Шекті-айырымдық схемалардың орнықтылығы мен жинақтылығы туралы түсінігі. Схеманың орнықтылығын зерттеу, фон Нейман әдісі.
- •14.Эйлер схемасының бірінші дифференциалдық жуықтауы (бдж немесе модификацияланған теңдеу). Бдж көмегімен схеманың орнықтылығын зерттеу.
- •16. Лакс, Лакс-Вендроф, «Чехарда», Мак-Кормак схемалары. Аппроксимация және басқа қасиеттері.
- •18. Екі өлшемді тасымал және/немесе диффузия теңдеулері үшін айқындалмаған айырымдық схемалар. Кранк-Николсон схемасы. Айнымалы бағыт әдісі.
- •27. Бюргерс теңдеуі үшін Лакс-Вендроф схемасы, Мак-Кормак схемасы. Олардың қасиеттері.
16. Лакс, Лакс-Вендроф, «Чехарда», Мак-Кормак схемалары. Аппроксимация және басқа қасиеттері.
Лакс схемасы келесі түрде беріледі:
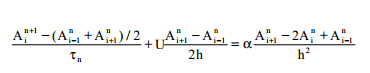
УАКО
схемасынан айырмашылығы уақыт бойынша
алынған туындының аппроксимациясы.Бұл
схемада уақыт бойынша алынған
![]() туынды орнына
туынды орнына
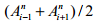 болады.Мұндай
алмастыруларды қолданғаннан сон қосымша
болады.Мұндай
алмастыруларды қолданғаннан сон қосымша
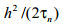 оң
мүшесі пайда болады.
оң
мүшесі пайда болады.
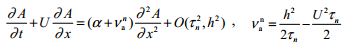
Лакс
схемасының орнықтылық шарты
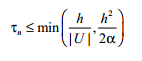
Лакс-Вендроф айқын орнықты екінші ретті схеманы ұсынды
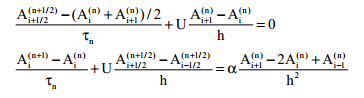 басқаша
жазатын болсақ
басқаша
жазатын болсақ
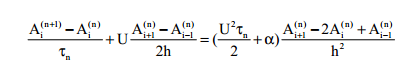 Мұнда
предиктор ретінде Лакс схемасы,ал
корректор ретінде Чехарда схемасы
қолданылады.
Мұнда
предиктор ретінде Лакс схемасы,ал
корректор ретінде Чехарда схемасы
қолданылады.
Чехарда
схемасы
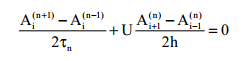
Тұтқыр мүшенің аппроксимациясы n-1 қабаты келесі түрде болғанда ғана орынды
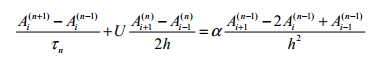
Демек
конвективті және диффузиялы уакыт
бойынша шектеулерді ескеру қажет

Келесі айқын классикалық әдістердің бірін Мак-Кормак ұсынған
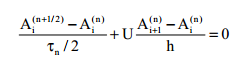
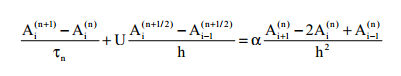
18. Екі өлшемді тасымал және/немесе диффузия теңдеулері үшін айқындалмаған айырымдық схемалар. Кранк-Николсон схемасы. Айнымалы бағыт әдісі.
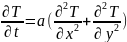 (1)
(1)
 (2)
(2)
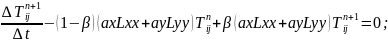 (3)
(3)
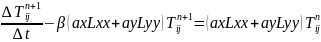 (4)
(4)
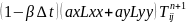 =RHS
(5)
=RHS
(5)
RHS=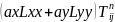
(5) теңдеу 5 диогональды матрицаға келгендіктен Томас алгоритмін қолдана шешу үшін 5 тен-ді келесі теңдеумен алмастырамыз.
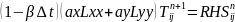 (6)
(6)
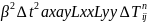 деген
артық мүше шығады.
деген
артық мүше шығады.
Х бойынша
 (7)
(7)
У бойынша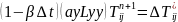 (7)
(7)
Ay=(ab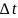 )
)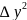
By=1+(2ab )
Ay=Cy
Ax=(ab
)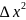
Bx=1+(2ab )
Ax=Cx
I этап( х бойынша)
-A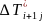 +B
+B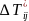 -C
-C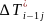 =RHS
=RHS
Ex=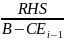
Fx=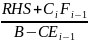
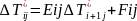
II этап( у бойынша)
-A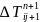 +B
+B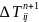 -C
-C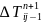 =
=
Ey=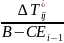
Fy=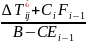
=E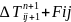
Айнымалы бағыт адісі;
(1)
1)
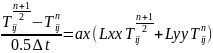
2)
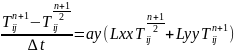
Кранк-Николсонның
схемасының аппроксимация қателегі
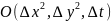 .Бұл
схема шартсыз орнықты болады.
.Бұл
схема шартсыз орнықты болады.
27. Бюргерс теңдеуі үшін Лакс-Вендроф схемасы, Мак-Кормак схемасы. Олардың қасиеттері.
Бюргерс теңдеуі
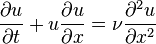 .
.
Егер
![]() деп алған жағдайда теңдеу келесі түрге
келеді
деп алған жағдайда теңдеу келесі түрге
келеді
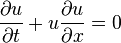 .
.
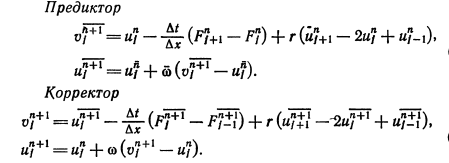
29. жалгасы
: Бастапқы-шекаралық есептер.
Мақсаты: Математикалық физика есептерінде бастапқы шекаралық есептерді дұрыс қоюға уйрету.
Математикалық физика есептерінде және жылуөткізгіштік есептердің дербес жағдайында, яғни шекараның есептелінетін облысының байламында шекаралық шарттың бірінші реті аппроксимацияланады. Екінші және үшінші ретті шекаралық шарттардың айырмашылығы, олардың айнымалы кеңістік бойынша ізделінетін функцияның бірінші ретті туындысы қатысады. Сондықтан, түрлі-шекті сұлбаның түйілісіне аппроксимация қажет. Бірінші ретті аппроксимация туындысының бағыты қарапайым нұсқа ретінде алынады:

Онда шекаралық жалпы жағдайының үшінші ретінің (2.7), (2.8) теңдеуі, түрлі сұлбаның екі шектік байламда ізделінетін функция мәні байланысады, сонда келесі өрнек түрінде беріледі:
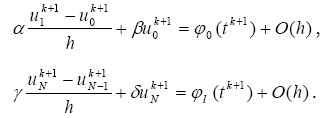
Шекті-әр түрлілігінің аппроксимациялық ішкі байламда белгілі теңдеуді аламыз, үшінші алғашқы-шектік есеп үшін белгілі әр түрлі сұлбаны аламыз (2.1), (2.4), (2.7), (2.8).

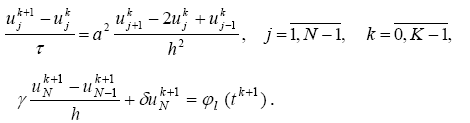
Жаңа
уақыттық қабатқа
![]() алгоритмдік
өтуін белгілі сұлбаның көмегімен аламыз:
алгоритмдік
өтуін белгілі сұлбаның көмегімен аламыз:
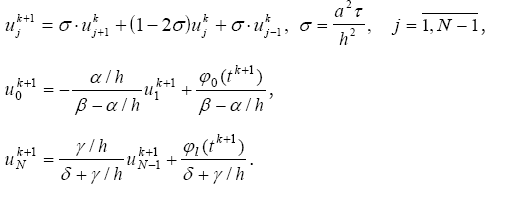
Яғни, алғашқы ізделінетін функцияның барлық ішкі жаңа уақыттық қабаты есептелінеді, содан соң шекарадағы мәндер анықталады.
Белгісіз соңғы-түрлі сұлбаны қолданып, дифференциалдық есепті аламыз:
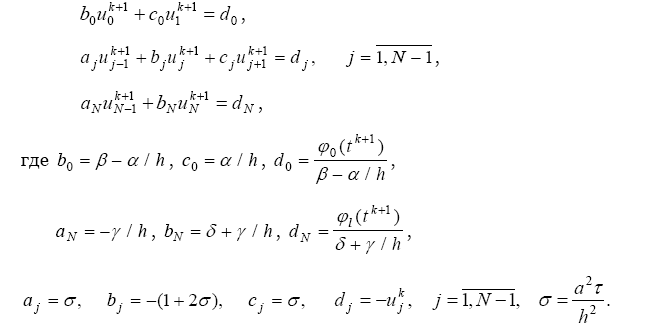
Нәтижесінде жаңа уақыттық қабаттың шешімін табу үшін сызықтық алгебра теңдеуінің үш-диагональді матрицалар жүйесін қолданамыз. Белгілі және белгісіз сұлбаны қолданған кезде осыған ұқсас болады.
Шекаралық шарттың бірінші ретті аппроксимациясы жоғарыда көрсетілгендей қасиетке ие болады. Т.с.с. ішкі байланысуының аппроксимациясы шекаралық байланысуы тәртібі аппроксимациясы орындалады. Аппроксимациялық ретінің сетканы түгел байламын глобальді аппроксимациялық реті деп аламыз.
Аппроксимация ретті жоғарлауының шекаралық шартының белгілі бір әдісі екінші ретін дифференциалдық есеп болып табылады:
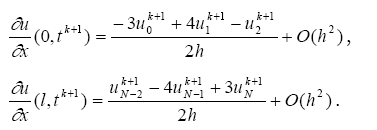
Егерде, белгілі сұлбаның алгоритімі есептің шешілуі жаңа уақыттың қабаты мен аппроксимациялық шекараның шартын қабылдамайды, бірақ принципиалдығы өзгермейді. САТЖ өзінің үш-диагональдығын жоғалтады егерде, белгісіз сұлба қолданылғанда(бірінші және екінші теңдікте үшеуі белгісіз болады). Үшінші теңдікті оңай алып тастау жолын қарастырамыз, яғни екінші және үшінші теңдіктерді комбинацияның сызықтық жолымен алуға болады. Бұл жағдайда диагональды матрицаның бұзылуы, сонымен қатар прагон әдісі де бұзылады.
Оны оңай жолымен қарастырайық, аппроксимациялық ретті шартын күшейтпелігінсіз аппроксимациялық қтынастың бйланыс саны. Иллюстрациялық подходты мынандай түрде көреміз.
Мысалы 2.1.
Үшінші
алғашқы-шектік есептің параболалық
теңдеуінде, құрамында конвекцияланған
мүшелерінің құрамдамасы,(туындының
пропорционалы
![]() ),
іздеу функциясының шығу көздері,
мүшелерін құрайды
),
іздеу функциясының шығу көздері,
мүшелерін құрайды
![]()
 (2.21)-(2.24)
Шешімі.
(2.21)-(2.24)
Шешімі.
Шекті-әртүрлігі сұлбасының теңдеуі, сетканың Шекті-әртүрлігінің белгісіз ішкі байланыста көреміз, (2.21):
 (2.25)
(2.25)
Егер,бірінші
тәртіптегі шекарлық шарттың туындысын
(2.22) және (2.23) аппроксимациялық сұлба
бойынша аламыз (оң және сол Шекті-әртүрлігін
қою-арқылы)

Онда
шекаралық шарттар бірінші тәртіп бойынша
аппроксимацияланады және глобальді
тәртібі, бірінші тәртіпке тең , барлық
қалған байланыс аппроксимациялық тәртіп
кеңістігі орын ауысуы екіге бөлінеді.
Аппроксимациялық тәртіпті сақтауға
және екіге теңдігін біз шекаралық
байланысуда дәл есептелінген теңдеуіне
қоямыз![]() сонда аумақ нүктесінде x=0 болғанда
Тейлор қатарына ауыспалы x үшінші
туындыға шейін ,
сонда аумақ нүктесінде x=0 болғанда
Тейлор қатарына ауыспалы x үшінші
туындыға шейін ,![]() -
аналогтық қатарының нүктелік ауданының
x=l деп аламыз(функциясының жазылуы
бойынша u(x,t) шекаралық байлаудан бірінші
туынды алынады және екіншіні х бойымен
аламыз):
-
аналогтық қатарының нүктелік ауданының
x=l деп аламыз(функциясының жазылуы
бойынша u(x,t) шекаралық байлаудан бірінші
туынды алынады және екіншіні х бойымен
аламыз):
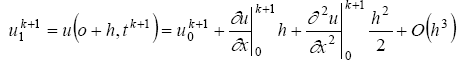 (2.26)
(2.26)
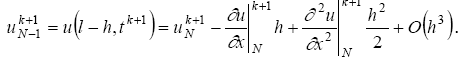 .
(2.27)
.
(2.27)
Әрі қарай екінші мәннің туындысын шекаралық байлануына қоямыз, дифференциалдық теңдеуін аламыз (2.21):
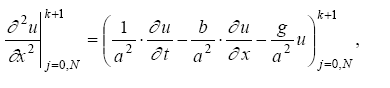
Алынған
өрнектен шығады
(2.26), бірінші
туындының мәнін шекаралық ретімен,
аламыз(2.27)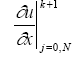
![]()

Қою
аркылы яғни
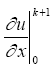 (2.22),
(2.22),
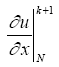 және
(2.23)
аппроксимациялық
кезінде
сәйкес қосылуы алынғанда шекаралык
байлануын қараймыз(осыдан алгебралык
теңдеудің шекаралық байланысуын аламыз,
осының әрқайсысында екеуі белгісіз
болады:
және
(2.23)
аппроксимациялық
кезінде
сәйкес қосылуы алынғанда шекаралык
байлануын қараймыз(осыдан алгебралык
теңдеудің шекаралық байланысуын аламыз,
осының әрқайсысында екеуі белгісіз
болады:
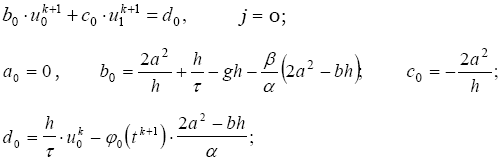 (2.28)
(2.28)
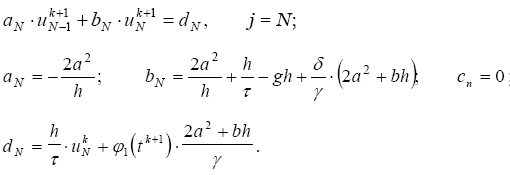 (2.29)
(2.29)
Осылайша,(2.28) - Шекті-әртүрлігінің аппроксимациясының шекаралық теңдеуінің үш түрі белгілі (2.22) сол жақ шекарада x=0 болады, яағни (2.29) - Шекті-әртүрлігінің аппроксимациялық үшінші-текті теңдеудің он жақ шекарада (2.23) x=l аппроксимацияның сол жақ ретін сақтайды, осылайша Шекті-әртүрлігінің аппроксимациясы (2.25) және дифференциалдық теңдеуінде де (2.21).
